Математика/ 5. Математическое моделирование

Д.т.н., академик КАН, А.В. Степанов

Южный филиал Национального университета биоресурсов и природопользования Украины «Крымский агротехнологический университет», Укаина

С.Н. Пушкарь

Старокрымский учебно-воспитательный комплекс № 1 «Школа-гимназия», Украина

О методах фильтрации аномальных уровней показателей в экономических рядах динамики

В задачах экономико-математического моделирования важное место занимают задачи прогнозирования значений таких важнейших показателей, как, например, объемы производства, объемы продаж, ставки процента, издержки и т.п. Известно, что временные ряды, по которым прогнозируются эти показатели, могут содержать такие элементы, как собственно тренд, сезонная вариация и циклическая вариация.

К сезонным явлениям относятся те, которые обнаруживают в своем развитии закономерности, более или менее повторяющиеся в определенные промежутки времени. Поэтому, при анализе сезонных явлений ставятся следующие задачи: численно выразить проявления сезонных колебаний, выявить факторы, вызывающие сезонные колебания, дать прогноз сезонных колебаний. Сезонные ряды можно представить аддитивно компонентами: тенденция (тренд), сезонные волны (кратковременные колебания) и помехи (случайные колебания). Случайные колебания вызываются внешними причинами, которые искажают тенденцию, а также сезонные и циклические колебания. Таким образом, задача прогнозирования состоит в выявлении закономерных изменений динамики составляющих временного ряда и далее их использовать для экстраполяции значений ряда на перспективу [1].

Основная проблема аппроксимации точечно-заданных кривых и поверхностей, значения в узловых точках которых, часто определяются с некоторым приближением или погрешностями, связана с выявлением и устранением, так называемых аномальных значений уровней ряда. Причинами аномальных уровней показателей могут быть ошибки технического порядка, возникающие при агрегировании и дезагрегировании показателей или при передаче информации, вследствие ошибочных измерений, округления численных значений и т.п., а так же в результате воздействия факторов, проявляющихся эпизодически. При этом возникает необходимость в процедурах «сглаживания» и согласования значений, сохраняя качественную «картину» описываемого объекта. К примеру, в одномерном случае, при аппроксимации необходимо сохранять вогнутые и выпуклые участки.

В настоящее время для выявления аномальных уровней используются методы, рассчитанные для статистических совокупностей, например, известные методы Ирвина, Фостера-Стьюарта или метод Шискина-Эйзеншпресса в задаче механической фильтрации [2].

Для сохранения качественной «картины» описываемого объекта, необходимо принять нетрадиционный подход, расчленив процесс аппроксимации на несколько этапов, применяя на его начальном этапе «цифровые» фильтры. Такая методика эффективна в одномерных случаях и частично переносится на сглаживание поверхностей (в частности, допускающих описание бикубическими сплайнами).

1. Постановка задачи. В прямоугольной системе координат узлы, являющиеся элементами некоторой поверхности, в проекциях на координатные плоскости и представляют некоторый точечно-заданный контур. Рассмотрим какую-нибудь одну из этих проекций. Например, проекцию на плоскость , положим, что она представляет собой следующий точечно-заданный контур:

Всюду в дальнейшем будем предполагать, что

Для выделения участков монотонности линии и проверки согласования вторых координат точек на выпуклых и вогнутых участках контура будем использовать разделенные разности первого

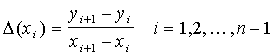
и второго порядков

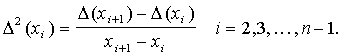
В дальнейшем будем предполагать, что мы имеем дело с контуром (или его частью) не содержащем «конструктивных» отрезков прямых. Такие отрезки, если они входят в состав контура, легко выделить согласно существующим методикам, и затем, в процессе аппроксимации, «состыковать» их со сплайновыми линиями, описывающими остальные участки контура. Поэтому в дальнейшем будем предполагать, что контур содержит только выпуклые и вогнутые участки.

Как отмечалось выше, вторые координаты точек часто бывают заданы с некоторыми погрешностями, что может привести к нарушению знаков величин и . Поэтому естественно попытаться на первом этапе согласовать знаки указанных величин, а потом перейти к построению сплайновой линии, имеющей выпуклые и вогнутые участки, соответствующие выпуклым и вогнутым участкам рассматриваемого контура, выделенным на первом этапе.

2. Классификация точек контура. Алгоритмы фильтрации. Предлагается метод фильтрации аномальных уровней, предполагающий на предварительном этапе классификацию точек некоторого контура , соединяющего экспериментальные данные, на основе рассмотрения значений:

где точки , и классифицируются как обыкновенные или точки перегиба.

Если , то точку будем называть обыкновенной точкой контура . Пусть . Тогда положим

где

Если или , то – обыкновенная точка контура . Если же , то – точка перегиба. Геометрический смысл классификации точек на обыкновенные точки контура и на точки перегиба приведен на Рис. 1-2. Частичный контур (Рис. 1.), состоящий только из четырех указанных точек, в случае обыкновенной точки должен быть выпуклым (или вогнутым).

Разделенные разности 1-го и 2-го порядков на , имеют вид:

Ясно, что при выполнении неравенства обыкновенная точка контура , а при выполнении соотношения точка точка перегиба.

Затем осуществляется классификация точек на «правильные» и «аномальные». Полагая для обыкновенных точек:

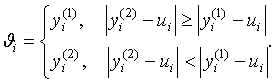
Если , то точку – аномальная и ее можно «исправить», полагая Аналогично классифицируются и исправляются точки перегиба.

Таким образом, на множестве последовательно находятся все аномальные точки, в которых определяются новые значения и разности . Для них вычисляется и ординате присваивается значение для исправления. Далее рассматривается новый контур:

,

на котором осуществляется новая итерация, аналогичная предыдущей и так далее. Процесс сглаживания заканчивается, когда на некотором контуре после итераций не останется ни одной аномальной точки. Если исходный контур не имеет неправильных точек, то число итераций, очевидно, будет равно нулю. Сглаженный контур будет состоять только из выпуклых и вогнутых участков и на нем знаки вторых разделенных разностей будут согласованы.

Заметим также, что «конструктивные» выпуклые и вогнутые участки должны иметь не менее пяти узлов во избежание их перестройки в процессе сглаживания. Любая точка на исходном контуре может быть заменена, если ей (независимо от ее характера) присвоить признак «правильная точка». Например, таким образом можно закрепить реальные точки перегиба. После завершения процедуры сглаживания контура фильтром можно дополнительно провести сглаживание вторых разделенных разностей путем применения еще одного фильтра с «плавающей» точкой перегиба и другой классификацией правильных и аномальных точек.

Предлагается программное обеспечение, основанное на реализации метода Шискина-Эйзенпресса, где в качестве цифровых фильтров используются средняя скользящая Спенсера и выпуклый фильтр, предложенный в работе [3]. Программа выполнена в среде С++ с учетом международных стандартов ANSI/ISO для С++ и имеет консольный интерфейс. Здесь используется система файлов, один из которых необходим для определения условия задачи, а остальные могут создаваться в процессе выполнения счета. В результате формируется текстовый файл, в котором поэтапно выводятся результаты расчетов. Программа максимально оптимизирована для использования. Здесь максимально снижена вероятность ошибок пользователя при вводе исходных данных. В результате тестирования, критических ошибок в работе программы не обнаружено.

SPP Seasonwave 1.0 имеет линейную структуру со встроенными циклами, предназначенными для проведения однотипных вычислительных операций над большим количеством элементов. Код программы содержится в трех файлах, два из которых файлы-библиотеки: lib.h (файл-заголовок) и lib.cpp (реализация библиотеки), а также основной файл реализации volna.cpp.

Программа составлена на основе принципов структурного программирования, и имеет ряд функций, которые определены в библиотеке. Здесь основные вычислительные функции библиотеки:

· void skolz_sredn(const int& l, const int& n, const int& m, ofstream& outs) – функция поиска скользящей средней;

· void skolz_spenser (const int& n, const int& l) – функция поиска скользящей средней Спенсера;

· make_lt(char uclov[массив], char vivod[массив], const int& l, const int& n) – поиск остаточных значений;

· make_lj(const int& n, const int& m) – поиск средних остаточных значений по месяцам (кварталам);

· make_l(const int& n) – поиск средних остаточных значений по ряду в целом;

· make_v1(const double& n, const double& l) – предварительная оценка сезонной волны;

· make_v2(const int& n, const int& m) – построение улучшенной оценки сезонной компоненты;

· make_U(const int& n, const int& m) – создание нового ряда, относительно свободного от сезонной компоненты;

· make_epsilant(const int& n, const int& m) – выделение случайной компоненты;

· make_k(const int& n, const int& m) – поиск коэффициента напряженности сезонной волны;

· result(const int& n, const int& m) – исключение окончательной сезонной волны.

Все вышеперечисленные функции используются в программе соответственно алгоритму Шискина-Эйзенпресса и алгоритму выпуклого цифрового фильтра [3] на выбор. Результат выполнения программы содержится в файле ot4et.txt в папке с исполняемым файлом программы. Все полученные таблицы, можно копировать и использовать в электронных таблицах MS Excel’XX.

Литература:

1. Эддоус М., Стэнсфилд Р. Методы принятия решений. – М.: Аудит: ЮНИТИ, 1997.

2. Федосеев В.В., Гармаш А.Н., Дайтбегов Д.М. и др. Экономико-математические методы и прикладные модели / Под ред. В.В. Федосеева, – М.: ЮНИТИ, 2002.

3. Степанов А.В. некоторые алгоритмы выравнивания временных рядов с использованием фактических значений уровней// Информационные модели экономики: сб. трудов II Всероссийской научно-практической конференции.– М., 2004.– С. 53-58.