Д.т.н., профессор «БашГУ»

Сулейманов Н.Т.

Башкирский государственный университет, Россия

Информационные модели оптической цепи волоконно-оптических преобразователей

Термины и критерии аналогии

информационной модели оптической цепи

Предлагается обобщенная модель процессов получения и преобразования информации в оптоэлектронных волоконно-оптических преобразователях, предполагая, что любой процесс в нем, независимо от физической природы, может быть представлен в виде совокупности элементарных преобразований одной физической величины в другую, каждое из которых может быть, в первом приближении, описан линейной зависимостью.

В процессе анализа и синтеза оптоэлектронного преобразователя в нем выделяются элементарные явления определенной физической природы (оптической, электрической, тепловой, магнитной, механической, диффузионной, акустической и т.д.), описываемых на основе физических эффектов и предполагается, что каждое такое явление есть реакция цепи рассматриваемой физической природы на воздействие на эту цепь.

Цепью определенной физической природы назовем материальную среду, имеющую геометрические размеры и характеризующиеся физическими контактами, присущими явлениям этой физической природы.

Для определения связи между воздействием и реакцией рассматриваемой цепи введем понятия величин воздействия и реакции, и понятия параметров цепи.

Величины служат для внешнего описания процесса и имеют различные значения для одной и той же цепи.

Параметрами характеризуют относительную неизменность материальной среды при отсутствии влияния соседних цепей другой физической природы.

В качестве обобщенных величин информационной модели приняты: величина воздействия (u), величина реакции (I), интегральная величина реакции – заряд (q).

В качестве обобщенных параметров информационной модели приняты: параметр сопротивления (R), параметр ёмкости (С) и параметр индуктивности (L).

Кроме перечисленных полезно ввести ряд производных понятий: параметр проводимости (), параметр жесткости () и параметр дедуктивности ().

Для выявления величин и параметров в цепях различной физической природы используют основные и производные критерии [1], которые представляют собой определенные элементарные зависимости между величинами и параметрами внутри цепи одной физической природы. В соответствии с этими критериями и физическими моделями, предложенными физиками для описания рассматриваемых процессов в цепи определенной физической природы, определяются величины и параметры этой цепи.

Критерий первый (энергетический). Произведение величины воздействия на величину реакции должно измеряться в единицах мощности независимо от природы процесса, протекающего в рассматриваемой цепи:

UI = P (1-1)

Критерий второй (критерий интенсивности). Величина реакции равна первой производной по времени от величины заряда

(1-2)

Критерий третий (статистический). Произведение величины реакции на параметр сопротивления равно величине воздействия

U = IR (1-3)

Критерий четвертый (динамический критерий первого рода). Величина реакции равна первой производной по времени от произведения величины воздействия на параметр емкости

(1-4)

Критерий пятый (динамический критерий второго рода). Величина воздействия равна первой производной по времени от произведения величины реакции на параметр индуктивности

(1-5)

Помимо основных критериев в ряде случаев используются производные от основных критериев:

- критерий, характеризующий процесс в ёмкости и заключающийся в равенстве величины заряда произведению величины воздействия на параметр ёмкости

q = UC (1-6)

- частичный случай критерия динамики первого рода, заключающийся в равенстве первой производной по времени от величины воздействия произведению величины реакции на параметр жесткости

(1-7)

при условии, что параметр жесткости (или ёмкости) в рассматриваемой цепи постоянен во времени (;

- частный случай критерия динамики второго рода, заключающийся в равенстве величины реакции произведению величины воздействия на первую производную по времени от параметра ёмкости

(1-8)

при условии, что величина воздействия неизменна во времени (u = const);

- частичный случай критерия динамики первого рода, заключающийся в равенстве первой производной по времени от величины реакции произведению величины воздействия на параметр, обратный параметру индуктивности (дедуктивность)

(1-9)

при условии, что параметр дедуктивности (или индуктивности) в рассматриваемой цепи постоянен во времени ();

- частичный случай критерия динамики второго рода, заключающийся в равенстве величины воздействия произведению величины реакции на первую производную по времени от параметра индуктивности

(1-10)

при условии, что величина реакции неизменна во времени (I=const).

Аналогия между геометрической оптикой и электронными траекториями в электрических цепях.

Основу геометрической оптики составляет закон преломления Снеллиуса, который гласит:

1. При переходе из одной среды в другую луч падающий, луч преломленный и перпендикуляр, восстановленный в точке падения к границе раздела двух сред, лежат в одной плоскости.

2. Между углом падения и углом преломления существует соотношение

(1-11)

где n₁ и n₂ – коэффициенты преломления, характеризующие обе среды.

Покажем теперь, что аналогичный закон описывает также движение электронов в электрическом поле, т.е. покажем, что существует тесная аналогия между световыми лучами и электронными тректориями в электрическом поле [5].

Можно приближенно имитировать действующую на электрон мгновенную силу, если создавать между двумя близко расположенными металлическими сетками соответствующую перпендикулярную к поверхности раздела напряженность электрического поля.

На рис. 1-1 две области постоянного потенциала I и II обозначены через I и II; переход от V₁ к V₂ происходит в области заключенной между двумя плоскостями F₁ и F₂. Пусть V₁ – скорость, с которой электрон, приходящий из области I, пересекает плоскость F₁ и V₂ – скорость, которую он имеет в области II, α – расстояние между плоскостями F₁ и F₂.

Используя уравнение Лагранжа второго ряда для движения электронов и отсчитывая потенциалы V₁ и V₂ от катода, и обозначив через ε скорость, с которой электрон покидает катод, получим значение скоростей V₁ и V₂:

(1-12)

где l – заряд; m – масса электрона.

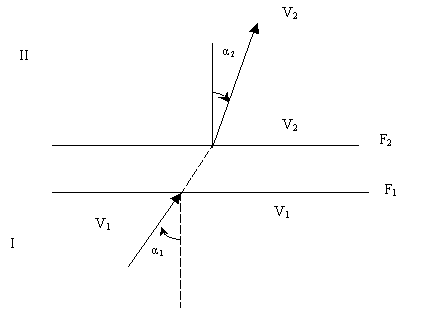
Рис. 1-1

Напряженность поля в переходной области F₁ и F₂

(1-13)

направлена перпендикулярно к F₁ и F₂, поэтому составляющая скорости V₁, параллельна этим плоскостям, не изменяется

тогда (1-14)

Отсюда следует, что

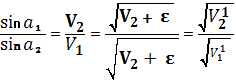(1-15)

Эта зависимость между и имеет ту же форму, что и закон преломления Снеллиуса

Где = с/, а = с/; - скорость света в среде I, - скорость света в среде II и с – скорость света в вакууме.

Такую же аналогию между геометрической оптикой и электронной оптикой можно показать при совместном действии электрического и магнитного полей на движение электрона. Отмечая аналогию между световой и электронной оптикой, следует отметить, что эта аналогия имеет вполне определенные границы, а именно:

1. В электрических и магнитных полях имеется не резкое, а постепенное, непрерывное изменение показателя преломления в электронной оптике, тогда как в геометрической оптике мы имеем скачкообразное изменение той же величины.

Причина появления такой ситуации с математической точки зрения вкратце состоит в том, что квадрат показателя преломления (пропорциональный потенциалу данной точки пространства) в электростатическом случае, при отсутствии объемного заряда, должен удовлетворять уравнению Лапласа Δ²n² = 0. Таким образом, показатель преломления должен представлять собой во всем пространстве, где происходит фокусировка рассматриваемых пучков частиц, непрерывную функцию координат, удовлетворяющую некоторым определенным, хотя и не очень жестким, условиям. В световой оптике эти ограничения отсутствуют, и мы можем по нашему произволу сопрягать по любым поверхностям раздела оптические среды с любыми, доступными нам показателями преломления.

2. Второе основное различие электронной оптики от обычной геометрической оптики заключается в том, что в то время как в оптике мы имеем дело с большим разнообразием веществ, обладающих различными оптическими свойствами, в электронной оптике такое разнообразие отсутствует. В оптике можно сравнительно просто подобрать нужный сорт стекла, для получения необходимого показателя преломления. В электронной оптике мы имеем дело только с электрическим и магнитным полями; как бы мы не меняли форму электродов и их потенциалы, взаимодействие электрона и поля остается тем же самым.

3. Между лучами света не существует взаимодействия аналогично тому электрическому и магнитному взаимодействию, которое имеется между пучками заряженных частиц, это различие тем существеннее, чем более плотность заряда в пучке.

Литература

1. Зарипов М.Ф., Сулейманов Н.Т., Петрова И.Ю. Надежность элементов и средств управления с распределенными параметрами. «Наука», М., 1980.

2. Харкевич А.А. Теория электроакустических преобразователей. Волновые процессы. I т.избр.труды, «Наука», М., 1973.

3. Сулейманов Н.Т., Надыров Р.Г., Нигматов Ж.М. Идентификация систем с определенными оптическими параметрами. В сб. Теория информационных систем и систем управления с распределенными параметрами. «Наука», М., 1978.

4. Зарипов М.Ф., Сулейманов Н.Т., Петрова И.Ю. Информационные модели и межцепные эффекты в оптических элементах систем управления. Академия наук СССР Уфимский филиал, Уфа, 1980.

5. Сулейманов Н.Т. Способы решения задач построения волоконно-оптических систем обнаружения несанкционированных врезок в магистральные трубопроводы. БашГУ, 2011.