Математика/5. Математичне моделювання

Елькін О.Б.

Харківський національний технічний університет сільського господарства ім.. Петра Василенка

Реалізація математичних моделей задач

призначення об’єктів та прокладки трас між ними

Задачі комбінаторної оптимізації з обмеженнями досить часто зустрічаються у таких різнобічних областях, як проектування радіоелектронної апаратури з розміщенням елементів та прокладкою трас між ними, упаковка геометричних об’єктів складної просторової форми, покриття області складної просторової форми заданими геометричними об’єктами, розбиття області складної просторової форми на під області з заданими властивостями та ін. Перелічені задачі відносяться до так званих задач геометричного проектування [1], розв’язок яких пов’язано з труднощами великого розміру шуканих параметрів, не лінійністю обмежень та функції мети, великої кількості локальних екстремумів. Все це вимагає розробки не тільки чисельних методів, але й апаратурного забезпечення для їх розв’язку.

Апаратна реалізація математичних моделей задач оптимізації варіантів призначення геометричних об’єктів на задані місця та прокладки трас, що з’єднують їх, здійснюється на базі сучасної спеціалізованої цифрової обчислювальної техніки. Це дозволяє ефективно здійснювати генерування [2, 3] та аналіз елементів відповідних комбінаторних множин, стосовно функції мети, сенс якої полягає у сумарних витратах на реалізацію проекту призначення геометричних об’єктів та трасування.

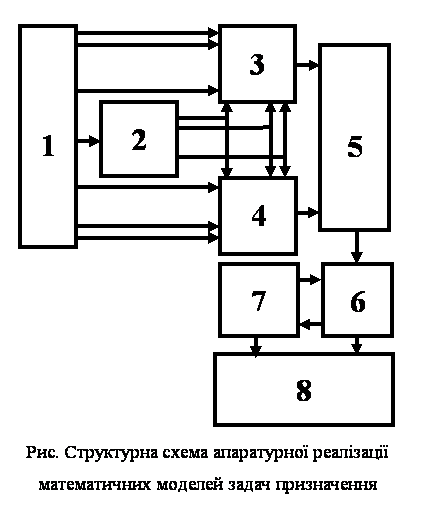
До апаратурної реалізації відповідних математичних моделей входять наступні основні блоки (рис.): блок 1 завдання вихідної інформації; блок 2 перебору сполучень, розміщень та перестановок; блок 3 обчислення функції мети за розміщенням; блок 4 обчислення функції мети за трасами; блок 5 обчислення загального значення функції мети; блок 6 пам’яті; блок 7 виділення мінімального значення функції мети; блок 8 реєстрації. У якості блоку генерування елементів комбінаторної множини є пристрій [3], решта блоків є стандартними.

При цьому попередньо, в залежності від задачі, що розв’язується, блок перебору сполучень, розміщень та перестановок [3] настроюється на генерування або перестановок, або сполучень, або розміщень. Потім задається вихідна інформація стосовно кількості об’єктів, що розміщуються, кількості місць можливого розміщення об’єктів, причому по одному на кожне місце.

Задається також матриця з’єднання об’єктів, кожний елемент якої вказує на наявність або відсутність зв’язку між об’єктами. Задаються коефіцієнти для оцінки загальної вартості розміщення об’єктів, та коефіцієнти для оцінки загальної вартості відповідних трас з’єднання об’єктів.

Далі здійснюється генерування елементів певної комбінаторної множини розміщень об’єктів. Кожний елемент цієї множини аналізується шляхом підрахування загальної вартості варіанту розміщення об’єктів та вартості відповідних трас. Ці значення вартості для кожного елементу комбінаторної множини запам’ятовуються, після чого визначається мінімальне значення загальної вартості та відповідний елемент комбінаторної множини, який вказує на найкращий варіант проекту розміщення об’єктів та проведення відповідних трас між ними.

За рахунок запропонованої апаратурної реалізації алгоритму розв’язання комбінаторних задач цього типу, витрати часу, у порівнянні з витратами часу на ПЕОМ, скорочуються у зв’язку з відсутністю етапу створення відповідного програмного забезпечення.

Скорочення часу розв’язання задач оптимізації на пристрої також забезпечується паралельним виконанням окремих етапів алгоритму, наприклад, обчислення функції мети за варіантом розміщення об’єктів виконується паралельно з обчисленням функції мети за відповідною структурою трас.

Загальний час розв’язання задач оптимізації та витрати пам’яті в основному залежать від кількості об’єктів, що розміщуються, кількості місць призначення об’єктів та характеру матриці зв’язків між об’єктами.

Точність розв’язання задач оптимізації за допомогою пристрою залежить від точності вихідних даних та точності виконання обчислювальних операцій цифровими блоками при розрахунку значення функції мети та її оптимізації.

Застосування такої спеціалізованої апаратури для розв’язання задач оптимізації проектування землеустрою, доріг, телекомунікацій, комунікацій загального призначення, дасть можливість знайти оптимальний варіант проекту, який забезпечить мінімальні витрати на його реалізацію.

Література

1. Стоян Ю.Г. Основная задача геометрического проектирования. – Харьков: ИПМаш АН УССР, Препринт №181. – 1983. – 36 с.

2. Курейчик В.М., Глушань В.М., Щербаков П.И. Комбинаторные аппаратные модели и алгоритмы в САПР. – М.: Радио и связь, 1990. – 216 с.

3. Авт. св. СССР № 643883. А 01 В 15/20 Устройство для перебора сочетаний, размещений и перестановок / Г.И. Левин  (СССР), 1979. Бюл. № 3.