Стельмашук Н.Т., Шилинец В.А., Правдиков П.И.

Белорусский государственный педагогический университет

РЕДУЦИРОВАНИЕ К ИНТЕГРАЛЬНОМУ УРАВНЕНИЮ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ В ФОРМАЛЬНЫХ ПРОИЗВОДНЫХ

Предметом исследования является следующее дифференциальное уравнение

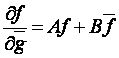, (1)

где

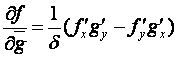, (2)

()

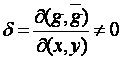в некоторой области ; – известные комплексные функции, заданные в области ; , , .

Дифференциальный оператор, определяемый равенством (2), называется формальной производной [1,2].

Для исследования дифференциального уравнения (1) нам потребуются функции, моногенные в смысле В.С. Фёдорова [3,4].

Определение 1. Комплексная или гиперкомплексная функция называется моногенной в смысле В.С. Фёдорова по функции в области , если в каждой точке области выполняется условие

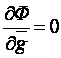. (3)

Заметим, что уравнению вида (1) при посвящён ряд работ. И.Н. Векуа функции, удовлетворяющие уравнению (1) при , назвал обобщёнными аналитическими функциями [5].

Целью настоящей работы является приведение (редукция) к интегральному уравнению уравнения (1) и исследование полученного интегрального уравнения.

Теорема 1. Уравнение (1) редуцируется к следующему интегральному уравнению:

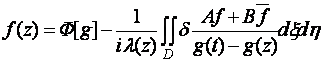, (4)

где , , , ; – функция, моногенная в смысле В.С. Фёдорова по в области ; ; определяется формулой (); ; – вариации относительно некоторой кривой , которая принадлежит области и содержит внутри себя точку .

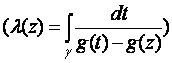Доказательство. 1. В работе [2] получено следующее интегральное представление:

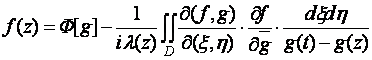, (5)

где – функция, моногенная в смысле В.С. Фёдорова по в области .

Используя формулу (), представление (5) запишем в виде:

. (6)

Из равенств (6) и (1) и получим интегральное уравнение (4).

Итак, если функция удовлетворяет уравнению (1), то она удовлетворяет интегральному уравнению (4).

2. Покажем, что если функция удовлетворяет уравнению (6), то она удовлетворяет и уравнению (1).

Введём обозначение

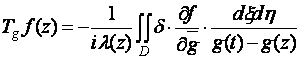, (7)

где .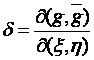

Как следует из работы [2],

. (8)

Из формулы (3) следует, что

. (9)

Из равенств (4), (6), (8) и (9) и вытекает последнее утверждение.

Имеет место также следующая теорема.

Теорема 2. Если

, ,

функция удовлетворяет в области условию

, , , , ,

то оператор

является вполне непрерывным в области .

Литература

1. Гусев В.А. Об одном обобщении ареолярных производных // Bul. stiint. al Instit. politehnic Timisoara. 1962. T.7. F.2. P.223-238.

2. Pascali D. Monogeneitatea Fedorov in plan // Studii si cercetari matematice Acad. RPR. 1964. T.16. №10. P.1231-1241.

3. Фёдоров В.С. Основные свойства обобщённых моногенных функций// Известия вузов. Математика. 1958. №6. С.257-265.

4. Стельмашук Н.Т., Шилинец В.А. Решение краевой задачи для одного класса функционально-инвариантных вектор-аналитических функций // Весцi НАН Беларусi. Серыя фiз.-мат. навук. 2006. №1. С.44-47.

5. Векуа И.Н. Обобщенные аналитических функций. М., 1959.