ВЫБОР НЕЧЕТКОЙ МОДЕЛИ ДЛЯ ПРОГНОЗИРОВАНИЯ

ДЕФЕКТОВ МЕТАЛЛОПРОДУКЦИИ

Кудинов Ю.И., Иванченко К.С., Кудинов И.Ю.

Липецкий государственный технический университет

В настоящей работе рассматриваются вопросы построения идентификации и выбора одной из трех типов нечетких моделей прогноза дефектов, металлопродукции (слябов), выпускаемой машиной непрерывного литья заготовок (МНЛЗ), схема которой изображена на рисунке.

Из стальковша жидкая сталь при температуре 1540 – 1580С^о подается в промежуточный ковш (промковш) и далее в два кристаллизатора. Каждый кристаллизатор заполняется сталью до определенного уровня х₁ и подвергается качанию с частотой х₅, линейным х₆, х₇, х₈ и угловым х₉, х₁₀, х₁₁ перемещениям по осям X, Y, Z, соответственно. Тем самым, обеспечиваются стационарные условия затвердевания слитка, его качество и безопасная работа установки. Кроме того, измеряются ток двигателя привода х₂, температура в датчике уровня металла (ДУМ) х₃, а также в первом х₁₅, втором х₁₆ и третьем х₁₇ слое кристаллизатора, скорость изменения уровня х₄, вибрация х₁₂ , нагрузка х₁₃ и скорость разливки х₁₄. После наполнения кристаллизатора сталью до заданного уровня начинают вытягивать два слитка через зоны вторичного охлаждения.

Вода на охлаждение слитка проходит через форсунки девяти зон охлаждения на внутреннюю поверхность слитка с расходом х₁₈ и давлением х₂₀ и на внешнюю поверхность слитка с расходом х₁₉ и давлением х₂₁. От выбора режима работы зоны охлаждения в значительной степени зависит качество слитка и соответственно сляба. Переменные х₁, х₂, … , х₂₁ будем называть входными, а выходными – 11 дефектов у_j, j = , изменяющихся в пределах от 0 до 4. К ним относятся: у₁ – сетчатая трещина; у₂ – паукообразная трещина; у₃ – ребровая трещина; у₄ – поперечная трещина; у₅ –продольная трещина и др. (всего 11 дефектов). Для прогноза дефектов в зависимости от входных переменных х_i, i = , МНЛЗ использовались три типа нечетких моделей [1], содержащих в правых частях правил константы

: если х₁ есть, х₂ есть,…, х₂₁ есть, то (1)

нечеткие множества

: если х₁ есть, х₂ есть,…, х₂₁ есть, то (2)

и линейные уравнения

: если х₁ есть, х₂ есть,…, х₂₁ есть, то (3)

где - количество правил в j-той нечеткой модели (); ,-нечеткие множества, характеризующиеся функциями принадлежности (ФП), , форма и расположение которых зависит от параметров .

Процесс построения нечетких моделей (1) - (3) включает выбор ФП и обеспечение адекватности с помощью алгоритмов идентификации.

Для описания нечетких множеств использовались колоколообразные ФП с шестью параметрами [2], обладающие гораздо большей гибкостью, чем другие аналитические зависимости.

Для обеспечения адекватности нечетких моделей (1) - (3) используются алгоритмы идентификации констант и коэффициентов линейных уравнений рекуррентным методом наименьших квадратов параметров ФП генетическим алгоритмом и количества правил методом минимаксного разбиения ФП. Близость заданной величины дефекта и рассчитанной по j – ой нечеткой модели для k – го набора данных (k = ) оценивалась средним значением модульной ошибки

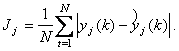
Идентификация нечетких моделей (1) – (3) проводилась по 1143 наборам данных для слябов, имеющих дефект – «поперечные трещины», и по 801 набору данных для слябов, имеющих дефект y₅ – «продольные трещины», с помощью программного комплекса [3], разработанного на кафедре информатики ЛГТУ и содержащего перечисленные выше алгоритмы идентификации. Результаты идентификации приведены в таблице.

Параметр	Модель (1)	Модель (2)	Модель (3)
n4 n5 J4 J5 n1 n4 J1 J4	6 5 0.276 0.346 4 4 0.18 0.44	10 5 0.169 0.158 5 5 0.29 0.29	5 7 0.141 0.053 2 2 0.01 0.12

Исходя из величины критериев , можно сделать следующий вывод: самую высокую точность прогноза дефектов дает нечеткая модель (3). Чтобы подтвердить полученные результаты, была проведена вторая идентификация нечетких моделей (1) – (3) по 619 наборам данных для слябов, имеющих дефект у₁ – «сетчатые трещины», и по 1165 наборам данных для слябов, имеющих дефект у₄ – «поперечные трещины». Результаты идентификации у₁, у₄, n₁, n₄ и J₁, J₄ приведены в таблице. Из таблицы видно, что все показатели нечёткой модели (3) (величина критериев J₁, J₄ и количество правил n₁, n₄) гораздо лучше, чем у моделей (1) и (2). Поэтому для целей прогноза дефектов металлопродукции целесообразно использовать нечёткую модель (3).

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Кудинов Ю.И., Венков А.Г., Келина А.Ю. Моделирование технологических и экологических процессов. – Липецк: ЛЭГИ, 2001. – 131 с.

2. Кудинов Ю.И., Келина А.Ю., Кудинов И.Ю., Суслова С.А. Построение и идентификация нечеткой модели многосвязного объекта // Вести высших учебных заведений Черноземья. – 2005. - №1. – С. 35-39.

3. Свидетельство РФ об отраслевой регистрации № 5768 от 26.02.06. Программный комплекс для построения нечетких моделей / Ю.И. Кудинов, И.Ю. Кудинов.