Современные информационные технологии/
2.
Вычислительная техника и программирование
К.т.н. Желтов
П.В., Семенов В.И., Шурбин А.К.
Чувашский государственный университет, Россия.
ПРИМЕНЕНИЕ НЕПРЕРЫВНОГО БЫСТРОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ ДЛЯ ОБРАБОТКИ ИЗОБРАЖЕНИЙ
В начале рассмотрим, как выполняется
дискретное вейвлет-преобразование (ВП) одномерных и двумерных сигналов.
Дискретное ВП не является дискретизированной версией непрерывного
вейвлет-преобразования. Если при непрерывном ВП используются сдвиги вейвлетов с
любым сколь угодно малым шагом, то дискретное ВП основано на использовании
целочисленных сдвигов и задании масштабов степени двойки. Как правило,
дискретные вейвлеты не имеют производных и при разложении в ряд Фурье имеют
длинные «хвосты». При дискретном ВП кроме вейвлета используется еще
масштабирующая функция. Масштабирующая функция и вейвлет вычисляются рекуррентно и не имеют аналитических
выражений.
Истоки дискретного ВП
восходят к 1976 году, когда был разработан метод
субполосного (пирамидального) кодирования речевого сигнала. При таком
кодировании сигнал пропускается через древовидное соединение ВЧ- и НЧ - фильтров. Сначала
сигнал пропускается через низкочастотный (low-pass) фильтр с импульсным откликом g, т. е. вычисляется свёртка. Одновременно сигнал
раскладывается с помощью высокочастотного (high-pass) фильтра h.
В результате получаются детализирующие коэффициенты (после ВЧ-фильтра) и
коэффициенты аппроксимации (после НЧ-фильтра). Эти два фильтра связаны между собой и называются квадратурными
зеркальными фильтрами (QMF). Так как
половина частотного диапазона сигнала была отфильтрована, то, согласно теореме
Котельникова, отсчёты сигналов можно проредить в два раза. Такое разложение
вдвое уменьшило разрешение по времени благодаря прореживанию сигнала. Однако
каждый из получившихся сигналов представляет половину частотной полосы
исходного сигнала, так что частотное разрешение удвоилось. Это разложение можно
повторить несколько раз для дальнейшего увеличения частотного разрешения с
дальнейшим прореживанием коэффициентов после НЧ- и ВЧ-фильтрации. Данное разложение можно представить в виде двоичного
дерева, где листья и узлы соответствуют пространствам с различной
частотно-временной локализацией. Это дерево представляет структуру банка
(гребенки) фильтров. На каждом уровне
сигнал раскладывается на низкие и высокие частоты. После двукратного
прореживания длина сигнала должна быть кратна 2n,
где n – число уровней разложения.
Восстановление сигнала происходит в обратном порядке, т. е. к детализирующим и
аппроксимирующим коэффициентам добавляются нулевые элементы, пропускаются через
зеркальные фильтры и складываются [1-4].
Для
синтеза масштабирующих и вейвлетных функций решается система уравнений для импульсных
характеристик фильтров, а по этим характеристикам рекуррентно вычисляются
масштабирующие и вейвлетные функции. Чем больше порядок вейвлета, тем система
уравнений сложнее. И. Добеши удалось найти метод,
позволяющий построить бесконечную серию ортогональных
вейвлетов, каждый из которых определяется конечным числом коэффициентов. Стало
возможным построить алгоритм, реализующий быстрое вейвлет-преобразование (БВП)
дискретных данных (алгоритм Малла).
Если объект является изображением, то функция z генерируется путем кодирования каждого пикселя M-строки и N-столбца
полутонами серого так, что более темные участки соответствуют меньшим
значениям, более светлые – большим значениям пикселя. Методы
вейвлет-преобразования подходят и для цветных изображений с тремя цветовыми
компонентами. Для этого необходимо выполнить вейвлет-преобразование независимо
на каждом из трех цветных компонентов изображения и представить результаты как
массив векторнозначных вейвлет-коэффициентов. Для дискретного двумерного
вейвлет-преобразования для многих приложений используется конструкция, в которой базисы вейвлетов получаются тензорным
произведением двух одномерных кратномасштабных анализов по столбцам и по
строкам. Различают стандартное и нестандартное построение двумерного базиса.
Стандартное построение двумерного базиса вейвлетов состоит во взятии
всевозможных тензорных произведений функций одномерного базиса. Для
стандартного разложения изображения нужно произвести одномерное преобразование
всех сток, а затем и всех столбцов. При
нестандартном построении двумерного базиса образуются одна скейлинк-функция и
три вейвлета, называемые горизонтальными, вертикальными и диагональными. В этой
конструкции низко- и высокочастотная фильтрация повторяется по строкам и
столбцам путем применения всех четырех возможных комбинаций. Дискретное
вейвлет-преобразование для нестандартного двумерного базиса задается схемой
![]() ,
,
где H – низкочастотная фильтрация,
G – высокочастотная фильтрация.
Индекс r означает, что фильтр применяется к строкам, а индекс
с – к столбцам. Если сигнал
(изображение) задан массивом N x N, то
каждый массив аппроксимирующих и детализирующих (для горизонтального,
вертикального и диагонального вейвлета)
коэффициентов первого уровня состоит из N/2 x N/2 элементов
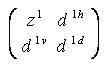 ,
,
где
![]() - аппроксимирующие коэффициенты,
- аппроксимирующие коэффициенты,
![]() с индексами h, v, d –
детализирующие коэффициенты.
с индексами h, v, d –
детализирующие коэффициенты.
Для второго уровня - N/4 x N/4 элементов, для третьего уровня - N/8 x N/8 элементов и т.д. Разложение сигнала на вейвлетные
ряды на заданном уровне разрешения m выполняется с использованием этих коэффициентов.
Авторами разработан алгоритм обработки изображений с применением
непрерывного




Рис. 1.
Кратномасштабный анализ изображения.
быстрого прямого и обратного ВП. При этом ВП осуществляется для всего
изображения, пилообразной разверткой по
строкам и столбцам. Так же можно применять и другие виды развертки, Так как
непрерывное ВП в разработанном алгоритме осуществляется в частотной области,
время обработки не значительное.
Например, для кратномасштабного
анализа цветного изображения размером 256 x256 пикселей достаточно 2 секунд. На рис. 1
представлены только 4 уровня декомпозиции из 16. По сравнению с дискретным ВП
изображений разработанный алгоритм прост и удобен. Так как для обработки
используются гладкие вейвлеты, которые имеют аналитическое выражение и
симметричны. Не нужно использовать ни интерполяции и децимации. Изображения
получаются на всех уровнях декомпозиции одинакового размера, равного размеру
исходного изображения. Каждый уровень разложения можно рассматривать отдельно
от других, а также несколько уровней вместе в зависимости от целей
исследования.
Литература.
1.
Столниц Э., Де Роуз Е.,
Салезин Д. Вейвлеты в компьютерной графике. Москва–Ижевск,
2002. 271 с.
2. Желтов П.В., Семенов В.И. Вейвлетные
функции// Компьютерные технологии и моделирование: сб. науч. тр. Чебоксары,
2008. Вып. 3. С. 60–65.
3. Семенов В.И. Свидетельство о государственной регистрации программы
для ЭВМ № 2011615828. Непрерывное быстрое прямое вейвлет-преобразование. Зарег.
в Реестре программ для ЭВМ 26 июля 2011
г.
4.
Семенов В.И. Свидетельство о государственной регистрации программы для ЭВМ №
2011615827. Ортогональное быстрое вейвлет-преобразование. Зарег. в Реестре
программ для ЭВМ 26 июля 2011 г.