физика/1. Физика твёрдого тела

Д.ф.-м.н Голев И. М., Усков А.В., Калиенко М.С., к.ф.-м.н. Янченко Л.И.

Воронежский государственный технический университет, Россия

Термоэдс и электрическая проводимость компактированных нанодисперсных углеродных материалов

В настоящее время интенсивно изучаются как методы получения, так и свойства наноразмерных углеродных материалов. Подобный интерес обусловлен большой перспективой их применения в качестве функциональных элементов в электронной технике, компонентов новых композиционных материалов.

Помимо исследования таких, ставшими уже «классическими», объектов как нанотрубки, фуллерены и нановолокна, интерес представляют также и нанообъекты размером более 30 нм. Особенностью частиц таких размеров является то, что значительное число атомов углерода расположены на поверхности и на краях, т.е. они имеют множество ненасыщенных связей [1]. Такие нанодисперсные углеродные материалы по химическим и физическим свойствам отличаются от замкнутых и закрытых систем, какими являются, например, фуллерены и нанотрубки.

В работе представлены результаты исследования термоэлектрических свойств структур, полученных компактированием материалов из углеродных частиц размером 30 - 120 нм (см. табл.)

Углеродные частицы	Размер частиц, нм
Наночастицы в аморфном состоянии	30–80
Деструктированный графит	Слои толщиной 30–100, длиной 10^4
Углеродные нановолокна (УНВ)	Диаметр 40–110, длина 500–2000
Микрочастицы в аморфном состоянии	80–120

Для измерения дифференциальной термоэдс методом горячего зонда (S) использовалась установка, представленная на рис. 1. Температура зонда изменялась в пределах 300 – 400 К с помощью электрического нагревателя. Сила прижатия зонда к поверхности образцов варьировалась в пределах 0,2 – 2 Н.

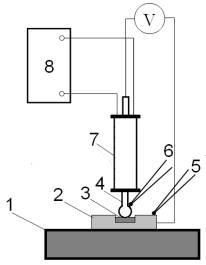
Рис. 1 Схематическое изображение установки для измерения термоэдс объемных образцов: 1 – массивное медное основание; 2 – серебряная подложка; 3 – образец; 4 – горячий электрод (серебряная проволока, d = 1 мм); 5,6 – термопара (ТХА); 7 – нагреватель, 8 – источник тока

На рис. 2 представлена схема для расчета распределения температуры в объеме исследуемых образцов между горячим зондом и подложкой.

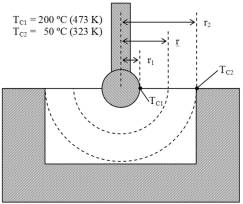
Рис.2 Схема теплопередачи между серебряной сферой горячего зонда и холодной подложкой через образец.

Тепловой поток через сферическую стенку радиусом выражается как:

, (1)

где и радиус и температура сферы горячего зонда, - расстояние от центра зонда до холодной подложки с температурой , - теплопроводность образцов, при расчётах принималась равной теплопроводности углерода 1,6 Вт·м^-1·К^-1.

Для обеспечения при измерениях значений температур =473 К, =300 К величина теплового потока Q должна быть не более Q = 2,4 Вт. Исходя из того, что плотность теплового потока:

(2)

равна q = 122,8·10³ Вт/м², можно построить зависимость температуры Т от расстояния от центра зонда r (рис.3).

Рис. 3 Зависимость температуры T от расстояния от центра зонда r

Из приведенных расчетов следует, что в экспериментах обеспечивается необходимый градиент температуры в объеме образцов, что позволяло проводить вычисления термо-э.д.с по формуле

, (3)

где ΔU и ΔТ – соответственно разность потенциалов и температур между горячей и холодной точками образца.

Измерения проводились в вакууме при давлении 10^-3 Торр. Нагрев осуществлялся со скоростью 2 градуса в минуту. С целью очищения углеродных материалов от адсорбировавшихся из воздушной среды молекул различных газов применялся отжиг при температуре 440 К в течение тридцати минут. При этом контролируемое электрическое сопротивление образцов переставало изменяться с течением времени.

Для калибровки установки проводились измерения температурной зависимости S для таких металлов: Cu (1,8 мкВ/К), Pt (– 5,3 мкВ/К) относительно серебра, имеющего значение термоэдс ~ 1,5 мкВ/К. Используемые образцы представляли собой пластинки толщиной 1,5 мм и площадью 25 мм². Полученные значения термоэдс совпадают с известными [2] с погрешностью не превышающей 5 %.

Рис. 4 Температурные зависимости коэффициента Зеебека (S) для микрочастиц углерода в аморфном состоянии (1), углеродных нановолокон (2), деструктированного графита (3) и наночастиц углерода в аморфном состоянии (4)

Результаты исследования компактированных материалов показали, что термоэдс при стандартных условиях равна: -7 мкВ/К для образцов из микрочастиц углерода в аморфном состоянии, -7,5 мкВ/К для образцов из углеродных нановолокон, -11,1 мкВ/К для образцов из деструктированного графита и -16,8 мкВ/К для образцов из наночастиц углерода в аморфном состоянии (рис.4).

Как известно, кристаллический графит состоит из плоских гексагональных сеток С₆. Формирование поли- и нанокристаллической структуры графита сопровождается уменьшением зерен и следовательно, размеров графеновых плоскостей, из которых состоит зерно графита. На границах зерен в местах обрыва гексагональных сеток образуется значительное количество периферийных атомов углерода, имеющих ненасыщенные связи. И, таким образом, образование зернограничной фазы в графите в значительном количестве приводит к росту термо-ЭДС.

В области температур, где проводимость s изменяется по активационному закону, экспериментальная температурная зависимость термо-эдс в неупорядоченных системах, как правило, описывается тем же выражением, что и для кристаллических полупроводников:

, (4)

где е - модуль электрического заряда, А - кинетический коэффициент, не зависящий от температуры, Es - параметр, имеющий размерность энергии.

Для нахождения температурной зависимости термо-э.д.с. в неупорядоченных структурах используется теория перколяции. В области действия закона Мота для прыжковой проводимости с переменной длиной прыжка термоэдс должна описываться формулой Звягина (5):

(5)

где g(E_F) и a – плотность состояний и радиус локализации на уровне Ферми.

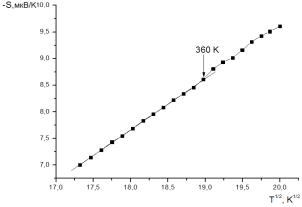
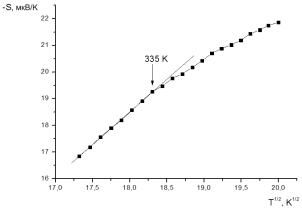
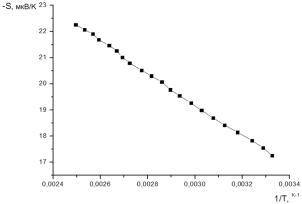
Для проведения анализа полученных результатов были построены зависимости (рис.5).

а) б)

в) г)

Рис.5 Зависимости для компактированного: микрочастиц углерода в аморфном состоянии (а), наночастиц углерода в аморфном состоянии (б), углеродных нановолокон (в) и деструктированного графита (г)

На рис. 5 представлены зависимости для образцов из наночастиц углерода в аморфном состоянии, микрочастиц углерода в аморфном состоянии и углеродных нановолокон, соответственно.

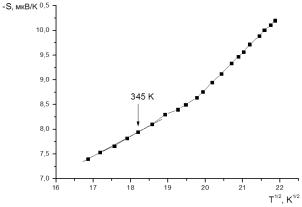
Как видно в области низких температур, где реализуется прыжковый механизм проводимости с переменной длиной прыжка, термоэдс имеет корневую температурную зависимость.

Температуры, при которых происходит отклонение от корневой зависимости составляют, 345 К для образцов из нановолокон, 360 К для образцов из микрочастиц углерода в аморфном состоянии, 335 К в случае образцов из наночастиц углерода в аморфном состоянии. Они несколько отличаются от температур, при которых происходит смена механизма электрической проводимости, что отмечается и в других исследованиях [3].

При повышении температуры характерна линейная асимптотика S ~ Т, как и в работе [4], которую можно связать с формулой Мотта для термоэдс [5]:

(4)

Для образцов из деструктированного графита термо-э.д.с пропорциональна 1/Т во всём температурном участке исследования (рис.5, г).

Возможное объяснение этих результатов можно связать с тем, что проводимости деструктированного графита что во всем диапазоне исследованных температур σ (Т) можно представить как сумму двух вкладов: прыжкового и активационного:

σ(Т) = σ_а(Т) + σ_h(Т), (5)

где σ_а(Т) – активационный вклад, σ_h(Т) – прыжковая проводимость.

Поэтому для электронного вклада в термоэдс при произвольной температуре справедлива формула (2):

, (6)

где S_h(T) и S_a(T) представляет собой вклады, отвечающие прыжковому и активационному законам проводимости.

Из результатов измерений проводимости видно, что у этого материала она превышает значения для других материалов в 6 - 10 раз. Из этого можно сделать вывод, что вклад существенно превышает вклад, обусловленный прыжковой проводимостью . Как следствие, температурная зависимость термоэдс определяется зависимостью , т.е. пропорциональна 1/Т.

Таким образом, результаты исследования температурной зависимости термоэдс свидетельствуют о том, что для исследуемых материалов при температурах доминирует прыжковый механизм электропроводности с переменной длиной прыжка, а также показано, что изменяя структурное состояние графита, можно создавать компактированные структуры с различной величиной электропроводности и термо-ЭДС. Это представляет интерес для использования в композиционных материалах, причем как в качестве наполнителя, так и в качестве матрицы.

ЛИТЕРАТУРА

1. Золотухин И.В., Голев И.М., Нефедов А.В., Усков А.В. Графены: методы получения и применение. Перспективные материалы. Москва, 2010. № 6. С. 5-11.

2. Бабичев А.П., Бабушкина Н.А., Братковский А.Н. и др. Физические величины: справочник. Под ред. Григорьева И.С., Мейлихова Е.З./ – М.: Энергоатомиздат. 1991. 1232 с.

3. Пронин А.А., Глушков В.В., Кондрин М.В., Ляпин А.Г., Бражкин В.В., Самарин Н.А., Демишев С.В. Прыжковая проводимость и магнитосопроивление наноматериалов на основе фуллерита C_2N, синтезированных в условиях высокого давления. Физика твёрдого тела, 2007, Т.49, В.7, С.1336-1342.

4. Демишев С.В., Кондрин М.В., Пронин А.А., Случанко Н.Е., Самарин Н.А., Ляпин А.Г., Бискупски Дж. Термо-эдс в области прыжковой проводимости. Переход от формулы Мотта к формуле Звягина. Письма в ЖТФ., Т. 68., В. 11, С. 801-806.

5. Звягин И.П. Кинетические явления в неупорядоченных полупроводниках. МГУ, 1984, 189 с.