Математика/5. Математическое моделирование

Д.м.н. Яцун С.М.

Курский государственный университет, Россия

Некоторые аспекты моделирования реакции кожи

на механическое воздействие

В дерматологии актуальной является проблема объективного инструментального контроля состояния кожного покрова [1,2]. Диагностика вязкоэластических свойств кожи затруднена из-за сложности ее морфологического строения. В связи с этим, наиболее приемлемым, а в некоторых случаях и единственным, являются неразрушающие методы контроля [3].

Механические свойства компонентов дермы во многом обусловлены растяжимостью ее эластиновых и коллагеновых волокон, их количественным соотношением и пространственной ориентацией. Для определения упруго-вязких характеристик кожного покрова создана математическая модель, описывающая взаимодействие исследуемого материала с электродинамическим генератором колебаний и системой датчиков, контролирующих процесс распространения малых возмущений.

С точки зрения математического моделирования, кожа представляет собой сложный неоднородный многослойный объект, поэтому для определения реакции кожного покрова далее рассматривается упрощенная математическая модель, которая основана на предположении о том, что кожа описывается дискретной моделью, содержащей две массы, связанные между собой упруго-вязкими элементами. Упрощенная расчетная схема представлена на рис.1. На схеме приняты следующие обозначения: m₁-масса бойка ударника (индентора); m₂, m₃ – приведенные массы слоев кожного покрова, участвующие во взаимодействии; с₁, с₂, с₃ – приведенные коэффициенты жесткостей слоев кожного покрова, участвующие во взаимодействии; b₁, b₂, b₃ – приведенные коэффициенты вязкого сопротивления в слоях кожного покрова; с_а, b_а – приведенные коэффициенты жесткости и вязкого сопротивления подвески индентора; x₁, x₂, x₃ – обобщенные координаты перемещения эпидермиса (x₁), собственно дермы (x₂), подкожно-жировой клетчатки (x₃).

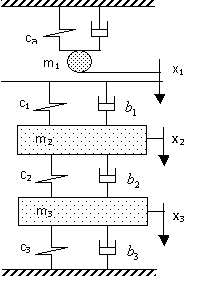
Рис.1. Упрощенная расчетная схема

Была построена математическая модель взаимодействия поверхности кожи с измерительным элементом. На первом этапе выполнены теоретические исследования с применением численного интегрирования дифференциальных уравнений математической модели. Эти исследования позволили определить параметры упругой подвески индентора, обеспечивающей безотрывное движение бойка по коже.

Анализ виброграмм показывает, что развитие возмущений в кожном покрове происходит с запаздыванием, т.е. сначала индентор деформирует поверхностный слой кожи, далее возмущение распространяется в нижележащие слои.

По результатам расчетов установлено, что перемещение бойка может быть приближенно описано экспоненциальным законом:

Х(t) = А₀·exp(-bt)·cos(wt),

где b – параметр, определяющий диссипативные свойства, w – параметр, определяющий упругие свойства кожи, А₀ – величина, определяемая начальными настройками упругой подвески индентора.

Идентификация коэффициентов b и w по экспериментально полученным данным позволяет количественно оценить упуго-диссипативные свойства кожного покрова.

Разработанная модель позволяет проводить численные исследования поведения упруго-диссипативных характеристик тестируемого материала с учетом взаимодействия экспериментальной установки и кожного покрова.

Статья выполнена в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» ГК№14.740.11.0249

СПИСОК ЛИТЕРАТУРЫ

1. Тимофеев, Г.А. Методы аппаратного исследования кожи человека // Косметика & медицина. – 2005, № 4. – С.28-36.

2. Яцун, С.М. Методы мониторинга объективных параметров кожного покрова // Медико-экологические информационные технологии: Сборник научных трудов.–Курск.–2007.С.105-112.

3. Yamamoto, T. Inthestigation mechanical of human skin. // Yamamoto T., Oka H., Narahashi N. / Clin Pharmacol. –1992, №5– С.2658-2663.