Економіка /Економіка промисловості

УДК 519.246.8:622.24

Фадєєва І.Г.

Івано-Франківський національний технічний університет нафти і газу

ПОСТАНОВКА ЗАДАЧІ ПРОГНОЗУВАННЯ СОБІВАРТОСТІ БУРІННЯ НАФТОВИХ І ГАЗОВИХ СВЕРДЛОВИН ЗА ДОПОМОГОЮ ШТУЧНИХ НЕЙРОННИХ МЕРЕЖ

Подальший розвиток нафтової і газової промисловості неможливий без суттєвого збільшення об’єму буріння свердловин. Тому, «Енергетичною стратегією України до 2030 року та подальшу перспективу» [1] передбачено до 2010 року збільшити обсяги пошуково-розвідувального буріння до 185 тис.м на рік, що майже у 6 разів перевищує фактичний обсяг пошуково-розвідувального буріння нових свердловин у 2004 році. Проведені розрахунки показали, що за час таких умов протягом прогнозованого періоду (2006-2030р.р.) можливо збільшити розвідані запаси в обсязі 63 млн.т нафти з газовим конденсатом.

Слушно відмітити, що буріння нафтових і газових свердловин – це складний технологічний процес, зв’язаний з великими витратами грошей і матеріальних ресурсів. Дійсно, майже 40% усіх капітальних вкладень в нафтову промисловість йде на буріння свердловин. Тому важливою і актуальною науково-практичною проблемою є прогнозування собівартості буріння нафтових і газових свердловин з метою досянення максимального економічного ефекту.

Слід зазначити, що для буріння свердловин витрачається значна кількість матеріалів: бурових доліт, труб, цементу, дизельного палива, хімреагентів для бурового розчину та ін. Своєчасна доставка цих матеріалів на бурові зв'язана зі значними транспортними витратами. Окрім того, характерною особливістю буріння нафтових і газових свердловин є висока собівартість і відносно висока тривалість виробничого циклу.

Враховуючи сказане, важливою задачею для буріння нафтових і газових свердловин є всебічне зниження витрат основних матеріалів, наприклад, за рахунок використання бурових доліт нового покоління типу PDC,а також зменшення витрат енергоресурсів за рахунок оптимізації процесу формування витрат.

Отже, прогнозування витрат на буріння нафтових і газових свердловин це задача прогнозування нестаціонарного стохастичного процесу, що функціонує за умов апріорної та поточної структурної і параметричної невизначеності [2].

З існуючих наукових досліджень [3,4] відомо, що методи, способи і методики прогнозування засновані переважно на двох підходах: евристичному і математичному (рис.1).

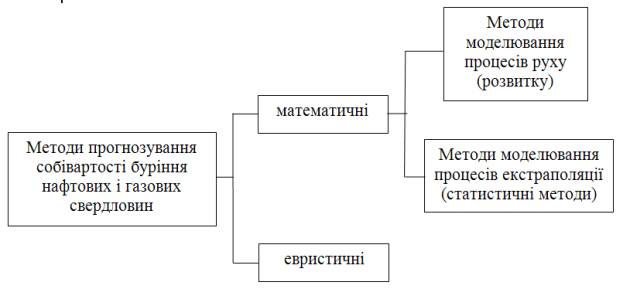
Рис.1 – Класифікація методів прогнозування собівартості буріння нафтових і газових свердловин

Безсумнівною перевагою евристичного прогнозування собівартості буріння, заснованого на використанні знань фахівців у даній області, є можливість уникнути значних помилок. Це пояснюється тим [3], що опитуються, як правило, висококваліфіковані фахівці в даній області знань. Проте, цей метод є суб’єктивним, досить складним і трудомістким у зв’язку з необхідністю об’єднання декількох прогнозів, які отримані від різних експертів. Таке завдання краще розв’язувати на базі методів інтелектуальних технологій прогнозування, наприклад, Fuzzy logic.

Основними перевагми математичних методів прогнозування собівартості буріння свердловин є об’єктивність одержуваної інформації, висока точність, а також можливість автоматизації процесу прогнозування. Проте, ці методи вимагають наявності чітко сформульованої математичної моделі поведінки прогнозованого об’єкту. Слід зазначити, що тільки у тому випадку, коли математична модель адекватно описує поведінку об’єкта, можна очікувати прийнятних результатів прогнозування собівартості буріння свердловини.

Окрім того, важливим етапом прогнозування є оцінка невідомих параметрів обраної математичної моделі – параметрична ідентифікація. Складність цієї задачі обумовлена зміною параметрів математичної моделі собівартості по мірі збільшення глибини свердловини.

Найчастіше при математичному прогнозуванні економічних чинників використовують математичні моделі Хольта-Уинтерса, Чоу, Бонса-Дженкінса, трендові моделі, метод Тригга-Лича та інші [4].

Оскільки загальновизнаним критерієм ефективності процесу буріння є собівартість одного метра проходки свердловини, скористаємось математичною моделлю собівартості метра проходки свердловини [5] для випадку, коли стійкість бурового долота лімітується опорами шарошкового долота:

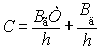, (1)

де С – собівартість одного метра проходки, грн/м;

Т – час, що витрачається на механічне буріння, спуско-підіймальні операції

і заміну бурового долота, год;

В_г – вартість 1 години роботи бурової установки, грн/год;

В_д – вартість долота;

h – проходка на долото, м.

Надамо модель (1), у якій прогнозована величина С явно виражається [3] через інші параметри моделі, у такому узагальненому вигляді:

G = f(d,x)+φ(b,x)ε , (2)

де f(d,x) і φ(b,x) – деякі детерміновані функції;

х – вектор відомих параметрів, однією зі складових якої є дискретний час

k=1,2,…,n;

d, b – вектори невідомих параметрів, що підлягають визначенню;

ε – випадковий незалежний процес (завада) з нульовим математичним сподіванням.

При бурінні свердловини в однорідних за міцністю породах з постійними параметрами режиму будемо вважати, що ε має постійну дисперсію, нормальний розподіл і є неавтокорельованим випадковим процесом.

В рівнянні (2) функція f(d,x) є детермінованою основою прогнозованої величини собівартості одного метра проходки. Вона характеризує значення величини С при відсутності випадкової завади ε.

Оскільки досліджуваний процес формування собівартості метра проходки свердловини є нелінійним для вирішення задач прогнозування доцільно застосування штучної нейронної мережі (ШНМ) як апроксиматора функції f(d,x), оскільки ШНМ є універсальним апроксиматором.

Враховуючи сказане і відомі методи прогнозування [6] на базі штучних нейронних мереж, задачу прогнозування сформулювали так: для нелінійної нестаціонарної послідовності,яка задана у формі часового ряду:

x(k) = (x₁(k),…, x_n(k))^T = (c(k-1),…, c(k-n)), k = 1,2,…,n , (3)

побудувати його прогноз

, (4)

де - прогноз часового ряду С(k);

f(x(k)) – невідомий оператор оцінювання;

k – поточний дискретний час.

Оскільки часовий ряд (3) поступає на вхід вейвлет-нейронної мережі, то вихід її описується виразом:

, (5)

де - вихід вейвлет-нейронної мережі;

- деякий оператор, що зв’язує простір входів з простором виходів.

Тоді завдання полягає в розробці методу прогнозування для визначення оцінки в момент часу k+d_h по даним передісторії k спостережень у реальному часі в темпі надходження даних, що забезпечують мінімум критерію якості

), (6)

за умов апріорної та потчоної невизначеності щодо природи і структури сигналу. Тут d_h – довжина упередження, або горизонт упередження.

Для практичної реалізації поставленої задачі прогнозування собівартості буріння нафтових і газових свердловин можуть бути використані відомі архітектури нейронних мереж та методи їх навчання.

Висновок

В роботі представлені результати, які у відповідності з поставленою метою є вирішенням актуальної задачі аналізу сучасного стану проблеми прогнозування нестаціонарних процесів і постановки задачі прогнозування собівартості буріння нафтових і газових свердловин за умов апріорної та поточної невизначеності.

Література:

1. Холявко М.П. Нафтогазовий комплекс України. Напрями реалізації основних положень енергетичної стратегії до 2030 року / М.П.Холявко // Хімічна промисловість України, 2007. - №2. – С.3-10.

2. Fadyeyeva I. New approfches to the desing of power retrenchment technologies in oil and gas well-drilling / I.Fadyeyeva, G.Sementsov // Proceedings East West Fuzzy Colloquium 2006 13^th Zittau Fazzy Colloquium, september 13-15, Zittau-2006. – p.49-54.

3. Сліпченко О.М. Нейронні мережі зі змінною кількістю вузлів у задачах обробки інформації: автореф.дис. на здобуття наук.ступеня канд.техн.наук: спец. 05.13.23 «Системи та засоби штучного інтелекту» / О.М.Сліпченко. – Харків, 2005. – 19 с.

4. Иванов В.В. Анализ временных рядов и прогнозирование экономических показателей / В.В.Иванов. – Харьков: ХНУ им. В.И.Каразина, 1999. – 229 с.

5. Александров М.А. Экономика бурения скважин долотами уменьшенного диаметра / М.А.Александров. – М.:Недра. – 1968. – 192 с.

6. Винокурова О.А. Прогнозування та емуляція нестаціонарних послідовностей за допомогою штучних вейвлет-нейронних мереж: автореф.дис.на здобуття наук.ступеня канд.техн.наук: спец. 05.13.23 «Системи та засоби штучного інтелекту» / О.В.Винокурова. – Харьків, 2005. – 19 с.