Экономические науки/ 8. Математические методы в экономике

Боднарюк І.Л.

ПВНЗ “Європейський університет”, Рівненська філія, Україна

Оптимізаційні задачі в економіко-математичному моделюванні витрат торговельних підприємств

В суто математичному плані деякі оптимізаційні задачі були відомі ще в стародавній Греції. Проте, історію розвитку математичного програмування в прикладних економічних дослідженнях, пов’язують із працями радянського вченого Канторовича Л.В., яким наприкінці 30-х років вперше були сформульовані основні задачі та критерії оптимальності, методи розв’язування, економічна та геометрична інтерпретація результатів розв’язування задач лінійного програмування.

Доцільним вважаємо визначитися із понятійним апаратом, що використовуватимемо в процесі постановки задач оптимізації витрат. Економічна енциклопедія трактує оптимальність (від латинської “optimus” – найкращий) як найкращий спосіб вирішення проблеми, економічної поведінки, економічних дій [1].

Критерій оптимальності визначається як система показників, що використовуються у різних галузях науки, техніки, економіки для обрання найефективнішого варіанта розв'язання певної задачі з кількох можливих варіантів. Принципи знаходження оптимального варіанта зводяться до того, щоб одержати максимальний ефект за даних витрат або досягти поставленої мети з мінімальними витратами [1].

Процес оптимізації пов’язаний із визначенням значень економічних показників, за яких досягається оптимум, тобто найкращий стан системи. Найчастіше оптимуму відповідає досягнення найкращого результату при даних витратах ресурсів або досягнення заданого результату при мінімальних ресурсних витратах [1].

Оптимальні норми дають можливість за даних техніко-економічних умов досягти найбільшої ефективності у використанні ресурсів або найповнішого задоволення економіко-господарських потреб країни (окремого суб’єкта господарювання). При розрахунках оптимальних норм використовують економіко-математичні методи, за допомогою яких визначають рівень, що забезпечує за певних обмежень досягнення заданого критерію [1].

Пошук реальних оптимальних норм чи показників ефективності господарської діяльності є, як правило, складною задачею і відноситься до екстремальних задач, в яких необхідно визначити максимум чи мінімум (екстремум) функції при визначених обмеженнях. Розв’язування екстремальної економічної задачі складається з побудови економіко-математичної моделі, підготовки інформації, отримання оптимального плану, економічного аналізу отриманих результатів і визначення можливостей їх практичного застосування.

Зауважимо, що в класичній постановці задачі математичного програмування передбачається одна цільова функція, яка кількісно визначена. У реальних економічних системах на роль критерію оптимальності (ефективності) претендують кілька десятків показників. Наприклад, максимум чистого доходу від реалізованих товарів у вартісному виразі чи максимум рентабельності, мінімум собівартості реалізованих товарів або мінімум витрат дефіцитних ресурсів.

Вимога досягти максимальної ефективності торговельної діяльності при мінімальних витратах як постановка математичної задачі є некоректною. Мінімальні витрати – нульові, що має місце при повній відсутності будь-якого процесу господарської діяльності. Аналогічно максимальна ефективність може бути досягнута лише у випадку понесення певних (звичайно не нульових) витрат. Тому коректними є постановки задач такого типу: досягти максимальної ефективності при заданих витратах чи досягти заданого ефекту при мінімальних витратах.

Представимо схематично систему оптимізації витрат торговельного підприємства (рис. 1).

Рис. 1. Система оптимізації витрат [2, с.10]

Параметри с_k (k=1, 2, ..., l) є кількісними характеристиками системи щодо наявності засобів праці (торговельних площ, живої праці, складських приміщень), рівня витрат і доходів підприємств торгівлі, продуктивності праці, ставок податків, процентів за кредит, цін на закупівлю товарів тощо.

Незалежні змінні бувають двох видів: керовані x_j – (j=1, 2, ..., n), значення яких можна змінювати в деякому інтервалі; некеровані змінні y_i (і=1, 2, ..., m), значення яких не залежать від діяльності підприємства і визначаються зовнішнім середовищем.

Кожна економічна система має мету (ціль) розвитку та функціонування F. Ступінь досягнення мети, здебільшого, має кількісну міру, тобто може бути описаний математично:

F = f (x_1, x₂, ..., x_n; y₁, y₂, ..., y_m, c₁, c₂, ..., c_l) (1)

В загальному вигляді задача математичного програмування формулюється так: знайти такі значення керованих змінних x_j, щоб цільова функція F набувала екстремального (максимального чи мінімального значення).

Отже, потрібно відшукати значення:

max (min) F= f (x_1, x₂, ..., x_n; y₁, y₂, ..., y_m, c₁, c₂, ..., c_l) (2)

Можливості вибору x_j завжди обмежені зовнішніми щодо системи умовами, параметрами економічної системи і т. ін.

Обсяг діяльності обмежений наявністю торговельних площ, продавців, купівельною спроможністю населення, необхідністю виконання договірних зобов’язань тощо. Ці процеси можна описати системою математичних рівностей та нерівностей виду

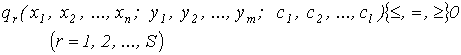(3)

Система (3) називається системою обмежень, або системою умов задачі. Вона описує внутрішні економічні процеси функціонування й розвитку торговельно-економічної системи, а також процеси зовнішнього середовища, які впливають на результат діяльності системи. Для економічних систем змінні х_j мають бути невід’ємними:

(4)

Залежності (2)-(4) становлять економіко-математичну модель економічної системи, розробляючи яку необхідно дотримуватися наступних правил: модель має адекватно описувати реальні економічні процеси; у моделі потрібно враховувати лише все істотне в досліджуваному процесі; модель має бути зрозумілою для користувача, зручною для реалізації на ЕОМ.

Оскільки не існує єдиного універсального критерію економічної ефективності, то досить часто вдаються до розгляду багатокритеріальної оптимізації. Багатокритеріальні задачі математичного програмування не мають універсального способу розв’язування. Отже, вибір та коректне застосування будь-якого з них залишається за суб’єктом прийняття рішень. Завдання математичного програмування полягає в представленні потрібної кількості науково обґрунтованої інформації, на основі якої здійснюється подальший вибір.

Література:

1. Економічна енциклопедія [Електронний ресурс]: Econom N&A, 2006. – Режим доступу: http://www.economna.com/content/blogsection/28/65/.

2. Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. – К.: КНЕУ, 2003. – 452 с.