Белов В. Т.

КЭИ ГВУЗ КНЭУ им. В. Гетьмана

О математической некорректности статистическо-вероятностной интерпретации волновой функции электрона

Введение.

В квантовой механике общепринятым является мнение о том, что волновая функция электрона не имеет никакого объективного физического смысла, а имеет только определенный математический смысл, а именно: величина является плотностью вероятности, а *dV дает вероятность найти частицу в объеме dV [1]. Так как волновая функция электрона является решением чисто физической задачи, то необходимо математически доказать, что действительно плотность вероятности какой-либо случайной величины [2]. Условие нормировки, использованное М. Борном, не является необходимым и достаточным условием существования случайной величины Х [2], плотностью вероятности которой была бы функция f(x)= Согласно [2] необходимым и достаточным условием того, что величина Х является случайной величиной, считается существование у величины Х интегральной функции распределения F(x). Так как М. Борн в [1] не дал такого доказательства, и в известной учебной и монографической литературе такого доказательства нет, то целью настоящей статьи является доказательство существования или не существования непрерывной случайной величины Х (НСВ Х) плотностью вероятности которой служила бы функция f(x)=

Теоретическая часть.

Согласно [2] величина Х является случайной величиной, если у нее существует интегральная функция распределения F(x),определяемая следующим образом:

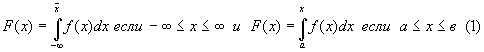
Причем имеют место следующие ограничения, накладываемые на функции F(x) и f(x):

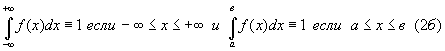
Для того чтобы существовал определенный несобственный или собственный интеграл (1) необходимо и достаточно, чтобы функция f(x) была непрерывной [3]. Согласно [3] функция f(x) считается непрерывной, если она в каждой точке интервала интегрирования имеет конкретное значение: f(xх)= f(х). Чтобы существовали интегралы (1) и (2) дополнительно необходимо, чтобы функция f(x) была ограниченной как снизу f(x), так и сверху f(x) [3]. Нижняя граница следует из свойств функции f(x) [2]: f(x). Верхнюю же границу определим из условия нормировки . Согласно теореме «о разложении единицы» [4] функция f(x) должна удовлетворять условию: f(x) . Так как теория вероятностей [2] не занимается невозможными событиями: f(x)= 0 и достоверными событиями f(x)=1, то окончательно имеем f(x).

В многочисленной учебной и монографической литературе [2, 5, 6] широко распространен случай, когда рассматривается f(x)=0, так называемый «парадокс нулевой вероятности». С точки зрения формальной логики это рассмотрение запрещено, так как невозможные события не являются предметом теории вероятностей. Покажем дополнительно, в чем заключается математическая ошибка такого рассмотрения.

Пусть действительная непрерывная случайная величина Х распределена на числовой оси действительных чисел в интервале от а до в

(в - а = L). Согласно [7] совокупность действительных чисел на ограниченном интервале числовой оси L представляет собой несчетное бесконечное множество, т. е. число возможных независимых исходов для действительной НСВ Х. В результате проведения испытаний конкретное значение Х = х появилось т раз, причем т представляет собой конечное счетное множество. Тогда вероятность того, что действительная случайная величина Х примет конкретное значение х равна . Итак, f(x=х₀)0 в чем и заключается смысл «парадокса нулевой вероятности».

Так как , то согласно [8] имеем дифференциальное уравнение , решением которого является функция , удовлетворяющая граничным условиям и . Подставляя в граничные условия х=а и х=в получаем: С=о и С=1. таким образом, полученная функция не удовлетворяет граничным условиям, т. к. постоянная С не может иметь два разных значения.

Итак, не существует такая НСВ Х, плотностью вероятности которой является f(x)=0, так как не существует соответствующая ей интегральная функция распределения .

Из рассмотренного доказательства вытекает следующее следствие: функция f(x) является рациональной функцией. Действительно, согласно [7] на ограниченном отрезке числовой оси от а до в имеется конечное счетное множество рациональных чисел, т. е. число всех независимых исходов n=N конечное счетное множество. Пусть в результате проведения испытаний конкретное значение Х = х появилось т раз. Тогда вероятность того, что рациональная случайная величина Х примет конкретное значение х равна: , т. е. f(x)>0. таким образом, условие 0<f(x)<1 является условием рациональности функции f(x).

Рациональность функции f(x) можно установить, пользуясь первичными понятиями аксиоматики теории вероятности [9], используя эмпирическую интерпретацию V аксиомы Колмогорова [10]. Итак, можно считать абсолютно твердо установленным, что для того, чтобы величина Х была случайной величиной и имела интегральную функцию распределения, ее дифференциальная функция плотности вероятности f(x) должна быть рациональной функцией, удовлетворяющей условию 0<f(x)<1.

Рассмотрим теперь, как удовлетворяется это условие для величины = f(x) в простейших задачах квантовой механики. Рассмотрим электрон, находящийся в бесконечно глубокой потенциальной одномерной яме шириной L. Волновая функция этой задачи и модуль ее квадрата в принятых в [11] обозначениях запишутся так:

*х; = *x…(2)

Положив L0,5* м – типично атомному размеру и взяв точку, х=0,5 и n=1 получим >>1.

Следующей более сложной, но точно решаемой задачей в квантовой механике является задача об электроне в атоме водорода. Согласно [11] волновая функция и ее квадрат могут быть записаны в 1S состоянии так:

= *е; = *е ……..(2)

Положив r= aм получим (r=a)5,3*10²⁷

Полученные в результате простейших расчетов числа, превышающие единицу на десятки порядков позволяют абсолютно точно утверждать, что величина является чем угодно, только не плотностью вероятности и статистическо - вероятностная концепция волновой функции электрона никакого отношения к теории вероятностей не имеет, т. к. не существует дифференциальной функции плотности вероятности f(x)>>1.

Обсуждение результатов.

Строгое математическое доказательство невозможности статистическо - вероятностной интерпретации волновой функции электрона не только ставит точку в давнем споре о смысле волновой функции электрона, но и порождает ряд вопросов физического и этического характера.

Очевидно, что волновая функция электрона имеет определенный физический смысл: в [12] было предложено, что волновая функция электрона описывает специфическую электромагнитную волну, которую создает движущийся электрический заряд-электрон, жестко привязанную к движущемуся заряду.

Сейчас по истечении продолжительного времени становится ясно, что корни статистическо - вероятностной интерпретации волновой функции электрона вытекают из философии Канта, широко распространенной в Германии в то время. Именно философия Канта позволила М. Борну получить Нобелевскую премию по физике за математическую ошибку. Неисповедимы пути твои Господи.

ЛИТЕРАТУРА:

1. Born M., Zeitsch. f. Phys., 38, 803 (1926).

2. Ширяев А. Н., Вероятность, М., Наука, 1980, с. 576.

3. Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления, М., 1966. Т.1, с.608, Т.2, с.807.

4. Владимиров В.С., Обобщенные функции в математической физике. М., 1979. с.468.

5. Д. Худсон, Статистика для физиков, М., Мир, 1970, 296 с.

6. Гмурман В. Е., Теория вероятностей и математическая статистика, М., Высшая школа, 2001г, с. 479

7. Александров П. С. , Введение в теорию многочленов и новую топологию, М., Наука, 1977, 368 с.

8. Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, М, Наука, 1981, с. 544.

9. Белов В. Т., Семенова Л. С., О первоначальных понятиях аксиоматики теории вероятностей, Киев, ТОВ. «Задруга», 2004, Материалы 10 международной научной конференции им. М. Кравчука, с. 1013.

10. Белов В. Т., Семенова Л. С., Эмпирическая интерпретация V аксиомы Колмогорова в теории вероятностей, Киев, ТОВ. «Задруга», 2006, Материалы 11 международной научной конференции им. М. Кравчука, с. 992.

11. Яворский Б.М., Детлаф А.А., Справочник по физике для инженеров и студентов вузов, М., 1965.с.848.

12. Белов В. Т., Физические основы динамической квантовой теории, Симферополь, 1992 г., Гортипография, Труды Крымского института аномальных явлений, т. 2, с. 56 - 74.