М.П.Ленюк
Обчислення невласних інтегралів
за власними елементами гібридного диференціального оператора Фур’є – Ейлера – Бесселя на полярній осі
Побудуємо обмежений на
множині
I![]() = {r: r Î (R0, R1)
= {r: r Î (R0, R1) ![]() (R1, R2)
(R1, R2) ![]() (R2, ¥); R0 ≥ 0}
(R2, ¥); R0 ≥ 0}
розв’язок сепаратної системи звичайних
диференціальних рівнянь Фур’є, Ейлера та Бесселя для модифікованих функцій
![]() , r Î (R0, R1),
, r Î (R0, R1),
![]() , r Î (R1, R2) (1)
, r Î (R1, R2) (1)
![]() , r Î (R2, ¥),
, r Î (R2, ¥),
за крайовими умовами
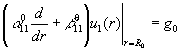 ,
, ![]() (2)
(2)
та умовами спряження
![]() ; j, k = 1, 2. (3)
; j, k = 1, 2. (3)
У рівностях (1) беруть участь диференціальні оператори Фур’є [1] L1=d2/dr2, Ейлера [1] 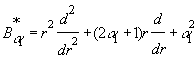 та Бесселя [2]
та Бесселя [2] ![]() = d2/dr2 +
= d2/dr2 + ![]()
Будемо припускати, що виконані умови на коефіцієнти:
qj>0, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() j,k=1,2.
j,k=1,2.
Фундаментальну систему розв’язків для диференціального
оператора Фур’є ![]() утворюють функції
утворюють функції ![]() та
та ![]() [1]; фундаментальну
систему розв’язків для диференціального рівняння Ейлера
[1]; фундаментальну
систему розв’язків для диференціального рівняння Ейлера ![]() утворюють функції
утворюють функції ![]() та
та ![]() [1]; фундаментальну
систему розв’язків для диференціального рівняння Бесселя
[1]; фундаментальну
систему розв’язків для диференціального рівняння Бесселя ![]() утворюють функції
Бесселя першого роду
утворюють функції
Бесселя першого роду ![]() та другого роду
та другого роду ![]() [2].
[2].
Наявність фундаментальної системи розв’язків дозволяє
побудувати розв’язок крайової задачі (1)-(3) методом функцій Коші [1,3]:
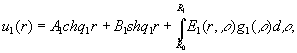
 (4)
(4)
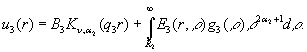
Тут ![]() - функції Коші [1,3]:
- функції Коші [1,3]:
![]()
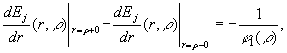 (5)
(5)
![]()
![]()
![]()
Припустимо, що функція
Коші
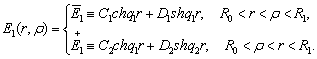
Властивості (5) функції Коші дають алгебраїчну систему:
![]()
![]()
Звідси знаходимо
співвідношення:
![]() (6)
(6)
Доповнимо рівності (6)
алгебраїчними рівняннями:
![]()
![]()
![]()
![]() (7)
(7)
Із алгебраїчної системи (6),(7) знаходимо, що
![]() ,
, 
Цим функція Коші E1(r,ρ) визначена й внаслідок симетрії відносно діагоналі r=ρ має структуру:
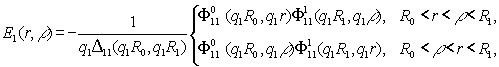 (8)
(8)
У рівностях (7)-(8) беруть участь функції:
![]()
![]()
![]()
![]()
Нехай функція Коші

Властивості (5) функції Коші
дають алгебраїчну систему :
![]()
![]()
Звідси знаходимо
співвідношення:
![]() (9)
(9)
Доповнимо систему (9)
алгебраїчними рівняннями:
![]()
![]()
![]() (10)
(10)
![]()
![]()
Із алгебраїчної системи
(10) маємо:
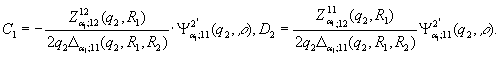
Цим функція Коші E2(r,ρ)
визначена й внаслідок симетрії відносно діагоналі r=ρ має структуру:
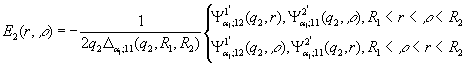 (11)
(11)
У рівностях (10)-(11)
беруть участь функції:
![]()
![]()
![]()
![]() .
.
Нехай функція Коші

Властивості (5) функції
Коші дають систему з двох рівнянь:
![]()
![]()
Звідси одержуємо
співвідношення:
![]() (12)
(12)
Доповнимо рівності(12)
алгебраїчним рівнянням
![]()
![]() (13)
(13)
Із алгебраїчної системи
(12),(13) знаходимо, що
![]()
Цим функція Коші E3(r,ρ) визначена й внаслідок
симетрії відносно діагоналі r=ρ має структуру:
 (14)
(14)
У рівностях (13),(14)
беруть участь функції:
![]()
![]() j=1,2,
j=1,2,
![]()
Крайова умова в точці r=R0 та умови спряження (3) для
визначення величин ![]() й
й ![]() дають алгебраїчну
систему з п’яти рівнянь:
дають алгебраїчну
систему з п’яти рівнянь:
![]()
![]() j=1,2
j=1,2
![]() j=1,2 (15)
j=1,2 (15)
У системі (15) беруть участь функції


та символ Кронекера ![]() [4].
[4].
Введемо до розгляду
функції:
![]()
![]() j=1,2,
j=1,2,
![]()
![]()
Припустимо, що виконана
умова однозначної розв’язності крайової задачі
(1)-(3): для будь-якого ненульового вектора ![]() визначник
алгебраїчної системи (15) [4]
визначник
алгебраїчної системи (15) [4]
![]() =
=
![]() (16)
(16)
Визначимо головні
розв’язки крайової задачі (1)-(3): 1) породжені крайовою умовою в точці r=R0 функції Гріна
![]()
![]()
![]() (17)
(17)
2) породжені
неоднорідністю умов спряження функції Гріна

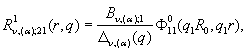
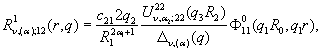
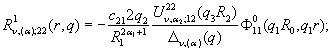
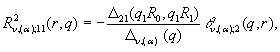

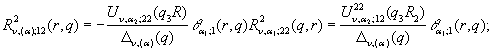
![]()
![]() (18)
(18)
![]() ;
;
3) породжені неоднорідністю
системи (1) функції впливу
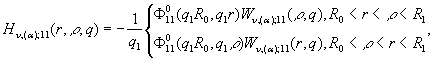
![]()
![]()
![]()
 (19)
(19)
![]()
![]()
![]()

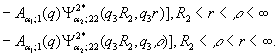
У результаті однозначної розв’язності алгебраїчної системи
(15) й підстановки отриманих значень A1,A2,B1,B2,B3 у рівності (4) маємо
(після низки елементарних перетворень)
єдиний розв’язок крайової задачі (1) – (3):
![]()


![]() . (20)
. (20)
Побудуємо тепер розв’язок крайової задачі
(1)-(3) методом інтегрального перетворення, породженого на множині ![]() гібридним
диференціальним оператором (ГДО)
гібридним
диференціальним оператором (ГДО)
![]() (21)
(21)
![]() одинична функція Гевісайда [3].
одинична функція Гевісайда [3].
Означення: За область визначення ГДО
![]() приймемо множину G
вектор
–функцій
приймемо множину G
вектор
–функцій ![]() з такими
властивостями 1) вектор-функція
з такими
властивостями 1) вектор-функція ![]() неперервна на множині
неперервна на множині ![]() ; 2) функції
; 2) функції ![]() задовольняють крайові
умови
задовольняють крайові
умови
![]()
![]() (22)
(22)
3) функції ![]() задовольняють умови
спряження
задовольняють умови
спряження
![]() j, k = 1, 2 (23)
j, k = 1, 2 (23)
![]()
Оператор Мν,(α)
самоспряжений й має одну особливу точку r
= ∞ [5]. Тому
його спектр дійсний та неперервний. Можна вважати, що спектральний параметр ![]() . Йому відповідає спектральна вектор-функція
. Йому відповідає спектральна вектор-функція
При цьому функції ![]() повинні задовольняти диференціальні рівняння
повинні задовольняти диференціальні рівняння
![]() r Î (R0, R1),
r Î (R0, R1),
![]() r Î (R1, R2), (24)
r Î (R1, R2), (24)
![]() r Î (R2, ∞),
r Î (R2, ∞),
![]()
Фундаментальну систему розв’язків для диференціального рівняння
Фур’є ![]() складають тригонометричні
функції v1=cosb1r та U2=sinb1r [1]; фундаментальну систему
розв’язків для диференціального рівняння Ейлера
складають тригонометричні
функції v1=cosb1r та U2=sinb1r [1]; фундаментальну систему
розв’язків для диференціального рівняння Ейлера ![]() складають функції
складають функції ![]() та
та ![]() [1]; фундаментальну
систему розв’язків для диференціального рівняння Бесселя
[1]; фундаментальну
систему розв’язків для диференціального рівняння Бесселя ![]() складають звичайні функції Бесселя
першого роду
складають звичайні функції Бесселя
першого роду ![]() та другого роду
та другого роду ![]()
![]() .
.
Якщо покласти
![]() r Î (R0, R1)
r Î (R0, R1)
![]() r Î (R1, R2),
r Î (R1, R2),
![]() r Î (R2,∞), (25)
r Î (R2,∞), (25)
то крайова умова в
точці r=R0 та умови спряження (23) для визначення шести величин ![]() дають алгебраїчну систему з п’яти
рівнянь:
дають алгебраїчну систему з п’яти
рівнянь:
![]()
![]()
![]() (26)
(26)
У системі (26) беруть
участь функції:
![]()
![]()
![]()
![]()
![]()
![]()
У результаті стандартного розв’язання алгебраїчної системи (26) [4] й підстановки величин Aj та Bj у рівності (25) маємо функції ![]() :
:
![]()
![]()
![]() (27).
(27).
У рівностях (27) прийняті
позначення:
![]()
![]() ,
,
![]()
![]() , j=1,2.
, j=1,2.
Визначимо спектральну
щільність [5]
![]() (28)
(28)
та вагову функцію [5]
![]() , (29)
, (29)
![]() ,
, ![]()
![]()
Наявність спектральної
функції ![]() , вагової функції σ(r) та спектральної щільності
, вагової функції σ(r) та спектральної щільності ![]() дає можливість
визначити пряме
дає можливість
визначити пряме ![]() й обернене
й обернене ![]() гібридне інтегральне
перетворення (ГІП),породжене на множині
гібридне інтегральне
перетворення (ГІП),породжене на множині ![]() ГДО
ГДО ![]()
![]() :
:
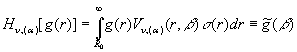 , (30)
, (30)
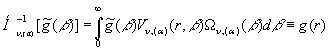 (31)
(31)
Тут ![]() Î G(область визначення ГДО
Î G(область визначення ГДО ![]() ).
).
Єдиний розв’язок крайової задачі
(1)-(3), одержаний за відомою логічною схемою [6] методом ГІП згідно формул (30),(31), має структуру:
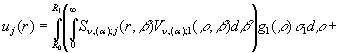
+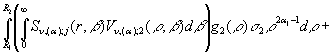
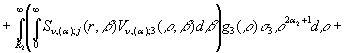
+

![]() (32)
(32)
У формулі (32) беруть
участь величини та функції:
![]()
![]()
Порівнюючи розв’язки (20) та (32) в силу єдиності, одержуємо наступні
формули обчислення поліпараметричних невласних інтегралів за власними
елементами ГДО ![]() :
:
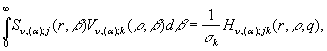
![]() , (33)
, (33)

![]() , (34)
, (34)

![]() ,
, ![]() , (35)
, (35)
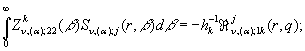
![]() ,
, ![]() , (36)
, (36)
Функції ![]() визначені формулами (19), функції Гріна
визначені формулами (19), функції Гріна ![]() визначені формулами (17), а функції Гріна
визначені формулами (17), а функції Гріна ![]() умов спряження
визначені формулами (18).
умов спряження
визначені формулами (18).
Зауваження 1.
Якщо ![]() , то
, то ![]()
![]()
![]() . В цьому випадку
. В цьому випадку ![]() ,
, ![]() ,
, ![]() і
і ![]()
Зауваження 2.
Якщо ![]() , то
, то ![]()
![]()
![]() . У цьому випадку
. У цьому випадку ![]() ,
, ![]() ,
, ![]() і
і ![]()
Зауваження 3.
Якщо ![]() , то
, то ![]()
![]()
![]() . У цьому випадку
. У цьому випадку ![]() ,
, ![]() ,
,![]() і
і ![]()
Зауваження 4.
Оскільки праві частини в рівностях (33)-(36) не залежать від нерівностей ![]() , то можна покласти
, то можна покласти ![]() звужуючи при цьому
сім’ю невласних інтегралів.
звужуючи при цьому
сім’ю невласних інтегралів.
Підсумком виконаного в роботі дослідження є твердження.
Теорема: Нехай вектор-функція ![]() неперервна на множині
неперервна на множині
![]() , а функції
, а функції ![]() задовольняють крайові умови (2) та умови спряження (3). Якщо
при цьому виконується умова (16) однозначної розв’язності крайової задачі
(1)-(3), то справджуються формули (33)-(36) обчислення поліпараметричних
невласних інтегралів за власними елементами ГДО
задовольняють крайові умови (2) та умови спряження (3). Якщо
при цьому виконується умова (16) однозначної розв’язності крайової задачі
(1)-(3), то справджуються формули (33)-(36) обчислення поліпараметричних
невласних інтегралів за власними елементами ГДО ![]() , визначеного рівністю (21).
, визначеного рівністю (21).
Відмітимо, що результати данної роботи (формули (33) – (36))
поповнюють довідкову математичну літературу [7].
Література:
1.
Степанов В.В. Курс
дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.
2.
Ленюк М.П. Исследование
основных краевых задач для диссипативного волнового уравнения Бесселя. – Киев,
1982. – 62 с. – (Препринт / АН УССР. Ин-т математики; 83.3).
3.
Шилов Г.Е.
Математический анализ. Второй специальный курс. – М.: Наука, 1965. – 328 с.
4.
Ленюк М.П., Шинкарик М.І. Гібридні інтегральні перетворення (Фур’є, Бесселя, Лежандра). Частина1.-Тернопіль: Економ.
думка, 2004.-368с.
5.
Курош А.Г. Курс высшей алгебры.-М.:Наука, 1971.-432с.
6.
Ленюк М.П. Обчислення невласних інтегралів методом гібридних інтегральних
перетворень (Фур’є, Бесселя, Лежандра).
Том V.Чернівці: Прут,
2005.-368с.
7.
Градштейн И.С., Рыжик И.М. Таблицы
интегралов, сумм, рядов и произведений. – М.:Наука 1971.-1108с.