К.т.н. Луценко М.О.

Національний технічний університет України “КПІ”, Україна

Визначення величини пружного переміщення інструменту при фрезеруванні 3–D поверхонь

При управлінні процесом фрезерування 3–D поверхонь первинною є задача стабілізації чи компенсації похибки, що викликана дестабілізуючими факторами. Лише потім вирішується задача удосконалювання (оптимізації) процесу по одному з критеріїв: максимальна продуктивність чи мінімальна собівартість. Рішення задачі стабілізації чи компенсації похибки, що викликана дестабілізуючими факторами здійснюється шляхом управління процесом обробки на верстатах із ЧПУ, за рахунок корекції еквідистанти чи управління режимами різання. При цьому управління процесом фрезерування на верстатах із ЧПУ повинно бути автоматичним і може реалізовуватися по збурюванню чи за похибкою. 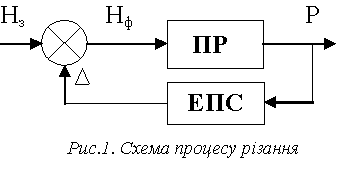У силу досить високої детермінованості процесу (відома інформація про форму поверхні деталі та заготовки, вихідної інструментальної поверхні та теоретичний закон руху інструмента відносно поверхні заготовки), управління по збурюванню, що припускає наявність адекватної моделі (а саме, передаточних функцій процесу різання (ПР) та еквівалентної пружної системи (ЕПС) див. рис.1), можна вважати найбільш ефективним для операцій фрезерування 3–D поверхонь.

При обробці 3–D поверхонь на фрезерних верстатах із ЧПУ процес різання є істотно нестаціонарним, що в сполученні з квазістаціонарністю передаточної функції еквівалентної пружної системи, приводить до утворення значної похибки обробки, викликаної, в основному, пружними переміщеннями ТОС. Розглянемо механізм виникнення пружного переміщення кінцевої сферичної фрези викликаного дією сили різання (рис.2).

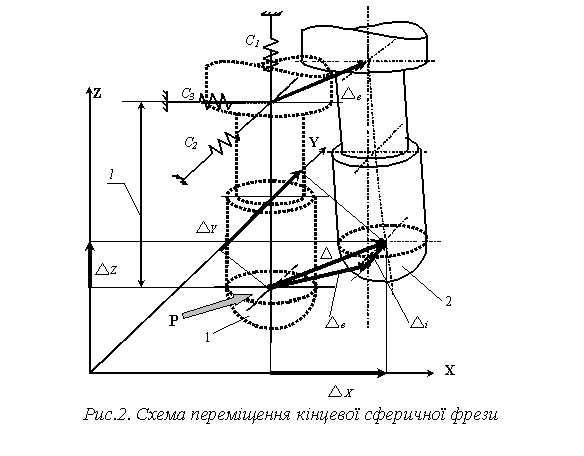
Траєкторія формоутворюючого руху розраховується для центра сферичної інструментальної поверхні кінцевої фрези (положення 1 на рис.2). При обробці заготовки, під дією сили різання P інструмент зміститься в положення 2. Величина переміщення Δ є величиною, що спрямована з центра теоретичного положення в центр фактичного положення сферичної поверхні інструмента. При цьому пружна система верстата представляється у вигляді трьох жорсткостей, що спрямовані вздовж осей прийнятої системи координат (наприклад, система координат деталі).

З геометричних побудов видно, що величина пружних переміщень складається з величини переміщення пружної системи верстата Δ₁ і переміщення Δ₂ інструмента. Переміщення інструмента виникає внаслідок вигину у площині XZ під дією проекції сили різання Р_X, вигину у площині YZ під дією складової сили різання P_Y і стиску (розтягуванню) у напрямку осі ОZ під дією складової сили різання P_Z. Таким чином, складові величини переміщення Δ у першому наближенні розраховуються за залежностями (перша складова є пружним переміщенням верстата: Δ_XВ, Δ_YВ, Δ_ZВ, друга – інструмента: Δ_XІ, Δ_YІ, Δ_ZІ, вздовж кожної з осей координат):

;

,

де I – усереднений осьовий момент інерції інструмента; F – усереднена площа поперечного переріза інструмента; d – усереднений діаметр інструмента; l – довжина вильоту інструмента; E – модуль пружності матеріалу інструмента.

Для більш повного врахування властивостей системи верстат-інструмент доцільно розглядати модель пружної системи верстату з орієнтованими осями жорсткості [1]. Ця модель пружної системи представляється у вигляді трьох жорсткостей С¹₁, С¹₂, С¹₃ (головні осі жорсткості), орієнтованих під деякими кутами щодо прийнятої системи координат (рис.3). На рис.3 жорсткості приведені до центра сферичної інструментальної поверхні фрези. Так як головні осі жорсткості не співпадають з прийнятою системою координат XYZ, а складові величини пружного переміщення мають бути представлені в прийнятій системі координат, тому важливою задачею є визначення величини пружного переміщення Δ в напрямку осей системи координат XYZ. Для вирішення цієї задачі можна скористатися наступною методикою.

62

Вхідними даними при цьому розрахунку є: сила різання, задана своїми проекціями в системі координат XYZ Р(Р_X;P_Y;P_Z); значення жорсткостей по головних осях жорсткості С¹₁, С¹₂, С¹₃ (система координат X¹Y¹Z¹) і орієнтація системи координат X¹Y¹Z¹ в системі координат XYZ:

i¹={a₁₁,a₂₁,a₃₁}; j¹={a₁₂,a₂₂,a₃₂}; k¹={a₁₃,a₂₃,a₃₃}

де, i¹, j¹, k¹ – ортонормований базис системи X¹Y¹Z¹, a₁₁..a₃₃ – проекції
i¹, j¹, k¹ в системі XYZ.

Першим кроком при розв’язанні поставленої задачі є визначення проекцій сили різання Р(Р_X¹;P_Y¹;P_Z¹) у системі координат X¹Y¹Z¹. Перехід від однієї системи координат до іншої здійснюється за такими залежностями:

Проекції величини пружного переміщення Δ_в в системі координат X¹Y¹Z¹:

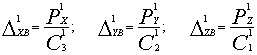
Виходячи з того, що розрахунки повинні узгоджуватися з прийнятою системою координат XYZ, у якій здійснюється формоутворення, необхідно визначити пружне переміщення, у напрямку осей цієї системи координат. Перехід від системи координат X¹Y¹Z¹, до системи XYZ для пружного переміщення Δ_в здійснюються за такими залежностями:

Отримані залежності дозволяють розрахувати пружне переміщення системи верстат-інструмент, що представляється моделлю з орієнтованими осями жорсткості.

1. Лазарев Г.С. Устойчивость процесса резания металлов. М., “Высшая школа”, 1973. – 184 с.