Карачун В.В., Мельник В.М.
Національний технічний
університет України «КПІ»
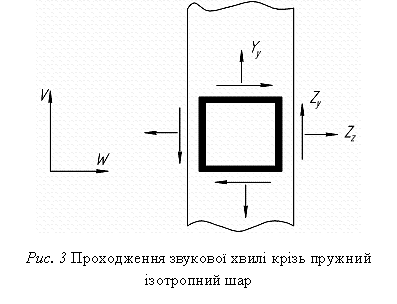
ОСОБЛИВОСТІ ДИФРАКЦІЇ ЗВУКОВИХ ХВИЛЬ
НА ПЛОСКІЙ ПЕРЕШКОДІ
Звуковий тиск
на лицьовій та тіньовій сторонах пластини обчислюється за допомогою виразів:

Для зручності розіб’ємо ці величини на симетричну ![]() (рис. 1) і
антисиметричну
(рис. 1) і
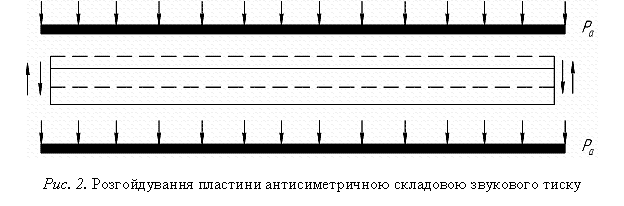
антисиметричну ![]() (рис. 2) складові і
з’ясуємо природу впливу кожної з них на виникаючі коливання поверхні пластини.
(рис. 2) складові і
з’ясуємо природу впливу кожної з них на виникаючі коливання поверхні пластини.

За дії симетричної складової надлишкового тиску, граничні умови
![]()
дозволяють
обчислити довільні сталі інтегрування ![]() з рівнянь (1)
з рівнянь (1)  де
де ![]()
![]()
і
з’ясувати закономірність примусового згинного руху пластини в напрямку товщини
–
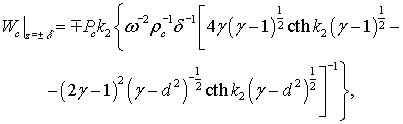 (2)
(2)
де ![]() .
.
Граничні умови при дії антисиметричної складової акустичної хвилі мають
вигляд –
![]()
а
згинний рух окреслюється виразом:
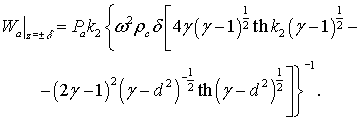 (3)
(3)
За умови, коли мають місце обмеження виду
 (4)
(4)
що
обумовлює присутність лише перших двох членів розкладання в ряд величин

у
співвідношеннях (4), (5), згин пластини під дією симетричної та антисиметричної
складових, відповідно, набуває виду –
 (5)
(5)
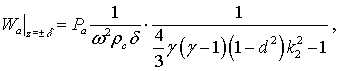 (6)
(6)
де  – швидкість
поздовжніх хвиль в пластині.
– швидкість
поздовжніх хвиль в пластині.
Вираз (5) співпадає з висновком Л.М. Лямшева для тих же умов.
Якщо ![]() , тоді перший доданок в знаменнику стає суттєво малим, у
порівнянні з одиницею, і формула (6) спрощується:
, тоді перший доданок в знаменнику стає суттєво малим, у
порівнянні з одиницею, і формула (6) спрощується:
 (7)
(7)
де 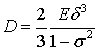 циліндрична
жорсткість пластини на згин;
циліндрична
жорсткість пластини на згин; ![]() – питома маса.
– питома маса.
Формула (7) відображує відомий закон згинних коливань
тонкої пластини.
Таким чином, коливання пластини під дією звукової хвилі, що падає під
кутом ![]() , аналітично описуються рівнянням руху тонкої пластини, якщо
довжина сліду падаючої хвилі (за умови
, аналітично описуються рівнянням руху тонкої пластини, якщо
довжина сліду падаючої хвилі (за умови ![]() ), або довжина поперечної хвилі (при
), або довжина поперечної хвилі (при ![]() ), складають 3,5 … 6 товщин шару.
), складають 3,5 … 6 товщин шару.
Зважимо ступінь впливу внутрішнього тертя в матеріалі пластини. В
першому наближенні це досягається введенням комплексного модуля Юнга
![]() ,
,
де ![]() – дійсна частина модуля пружності;
– дійсна частина модуля пружності; ![]() – коефіцієнт втрат.
– коефіцієнт втрат.
Під
внутрішнім тертям будемо розуміти сукупність будь-яких процесів в конструкції,
що слугують необерненому розсіянню механічної енергії при деформації.
З огляду на
зазначене, величина імпеданса для симетричної і антисиметричної складових
звукового тиску буде складати:
 (8)
(8)
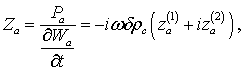 (9)
(9)
де ![]()
![]()
Порівняльний
аналіз динамічного і статичного модулів пружності, наприклад, сталі, довів, що
динамічна жорсткість її не відрізняється від статичної. Однак це не стосується
м’яких матеріалів, де потрібно враховувати зміну динамічних параметрів.
Отже,
використовуючи вирази (2), (3), можна встановити закон руху будь-якого прошарку
умовної пластини. Деяка незручність одержаних формул полягає в тому, що
переміщення пластини постає функцією симетричної і антисиметричної складових
тиску, а не амплітуди тиску падаючої хвилі ![]() .
.
Цього
недоліку легко позбутися скориставшись поняттям коефіцієнта проходження звука А та коефіцієнта відбиття В, пам’ятаючи, що перший дорівнює
відношенню тиску ![]() в пройдешній до тиску
в падаючій хвилі
в пройдешній до тиску
в падаючій хвилі ![]() , а другий – відношенню тиску
, а другий – відношенню тиску ![]() у відбитій хвилі до
тиску
у відбитій хвилі до
тиску ![]() .
.