Кудайкулов А.К., Атантаева С.А.
Евразийский национальный
университет им. Л.Гумилева, Казахстан
Решение задачи термо-напреженного
состояния защемленного двумя концами теплоизолированного стержня при
воздействии теплового потока и теплообмена
В работе на основе закона сохранения
энергии в сочетании применения апроксимационных сплайн функции построена
аналитическое решение установившейся задачи теплопроводности и
термо-напряженного состояния для стержня ограниченной длины, боковая
поверхность которого теплоизолирована. На площадь поперечного сечения левого
конца подведен тепловой поток, а через правого конца происходит теплообмен с
окружающей средой.
Рассмотрим горизонтальный полный стержень
ограниченной длины l
[см] . ось ох направим слева на право которая совпадает с осью стержня .
Площадь поперечного сечения стержня обозначим через F [см2] и считаем постоянной по всей длине,
материал стержня характеризуется коэффициентом теплопроводности Kxx
[Вт /(см2 ◦С ], коэффициентом теплового расширения α
[1/◦ С] и модулем
упругости Е![]() .
.
Боковую поверхность стержня считаем
теплоизолированной. Пусть на площадь
поперечного сечения левого конца стержня подведен тепловой поток постоянной
интенсивности ![]() . Через площадь поперечного сечения правого конца стержня
происходит теплообмен с окружающей этой площадью средой. При этом коэффициент
теплообмена
. Через площадь поперечного сечения правого конца стержня
происходит теплообмен с окружающей этой площадью средой. При этом коэффициент
теплообмена ![]() , а температура окружающей среды
, а температура окружающей среды ![]()
Требуется:
1) Для рассматриваемого стержня необходимо определить поле распределения
температуры с учетом всех имеющихся факторов
2) Если левый конец стержня жестко - защемлен,
а правый свободен, то необходимо определить величину удлинения рассматриваемого
стержня
3) Если оба концы стержня жестко-защемлены, то
необходимо определить поле распределения упругих, температурных и термо-упругих
составляющих деформации и напряжении, а также величину сжимающего усилия.
 Для решения поставленной задачи, сначала
рассмотрим расчетную схему (рис-1)
Для решения поставленной задачи, сначала
рассмотрим расчетную схему (рис-1) ![]()
![]()
Для рассматриваемой
задачи построим функционал полной тепловой энергии ![]()
![]()
![]() (1)
(1)
где ![]() площадь поперечнoго
сечения
левого и правого концов стержня соответственно; V- объем стержня
площадь поперечнoго
сечения
левого и правого концов стержня соответственно; V- объем стержня
С учетом физической
специфики задачи поле распределения температуры по длине стержня аппроксимируем
полным полиномом второго порядка
![]()
![]() (2)
(2)
Теперь введем следующие
обозначения
 (3)
(3)
Кривая, которая описывается (2) приводится на
(рис-2) 
![]()
![]()
Рисунок 2. Апроксимация поле распределения температуры
Пользуясь (3) из (2) получим следующую
систему уравнении
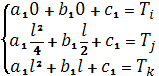 (4)
(4)
Отсюда определим
![]()
![]() (5)
(5)

Теперь подставляя
значения а1, в1,с1 (2) находим, что
![]()
( 6)
Где ![]() – аппроксимационные
сплайн функции которые имеют следующий вид
– аппроксимационные
сплайн функции которые имеют следующий вид
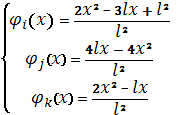 (7)
(7)
Эти функции имеют
следующие свойства :
 ;
;  ;
; 
(8)
Эти свойства сплайн
функции обеспечивает непрерывности поле распределения температуры по длине
стержня. Пользуясь соотнашениями (6-7)находим выражение градиента температуры
![]() (9)
(9)
Теперь вычислим отдельно
интегралы в выражении
![]()

(11)
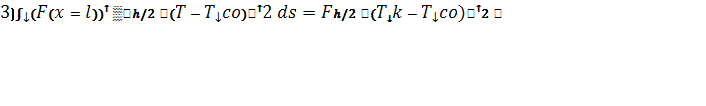
(12)
Теперь подставляя
(10-12) в (1) находим интегрированный вид функционала J.
![]()
![]() (13)
(13)
По закону сохранения
энергии при правильных значениях узловых температур ![]()
![]()
![]() функционал
функционал ![]() достигает своему
минимуму [1-2]. Отсюда получим следующую разрешающую систему уравнении
достигает своему
минимуму [1-2]. Отсюда получим следующую разрешающую систему уравнении
1) ![]()
2) ![]()
3) ![]() (14)
(14)
Здесь следует отметить,
что в этой системе сумма коэффициентов
при температуре будет равно нулю, т.е.
1) (14-16+2)=0
2) (-16-16+32)=0
3) (2-16+14)+Fh-Fh=0 (18)
Эти равенства являются
признаками выполнения закона сохранения энергии, т.е. полученная разрешающая система уравнении являются правильными и
они адекватно описывают исследуемый процесс.
Отсюда определим ![]()
![]()
![]()
(15)
Теперь подставляя найденные
значения Ti, Tj
,Tk в
выражения (6) после соответствующего упрощения получим закон распределения
температуры по длине исследуемого стержня
 (16) Где
(16) Где ![]()
![]() (17)
(17)
Из (16) видно что закон распределения температуры по
длине исследуемого стержня будет линейный. Хотя в начале мы эти
распределения аппроксимировали полным
полиномом второго порядка.
Таким образом, видно,
что применение закона сохранения энергии приводит самокорректировке получаемых
решении.
Теперь переходим к решению второго этапа
задачи т.е определим величину удлинения
стержня за счет поле распределения температуры по длине .
По основному закону
термодинамики удлинение стержня за счет поле распределения температуры
определяетя следующим образом
![]()
(19)
Но в общем случае
коэффициент теплового расширения материала стержня зависит от температуры ,т.е ![]() Предполагая, что для некоторых материалов значение
Предполагая, что для некоторых материалов значение ![]() при определенных
интервалах температуры можно принимать постоянной величиной из (19) и (16)
получим
при определенных
интервалах температуры можно принимать постоянной величиной из (19) и (16)
получим
![]()
(20)
Если, ![]() будет зависеть от
температуры, то эта зависимость для каждого материала
определяется отдельно эксперементальным путем.
будет зависеть от
температуры, то эта зависимость для каждого материала
определяется отдельно эксперементальным путем.
Но
в этом случае удлинение стержня определяется по формуле (19)
Теперь
предпологая, что обе концы стержня жестко-защемленной переходим к решению 3-го
этапа задачи. В этом случае из-за поле распределения температуры стержень не
может удленяться, но возникает сжимающее усилия термонапряженное состояния.
Этот
этап задачи можно решать двумя методами
1-й метод решения задачи
В этом случае для защемленного двумя
концами исследуемого стержня напишем выражение потенциальной энергии упругих
деформации с учетом наличия поля распределения температуры
![]()
(21)
Где
![]() - поле пере перемещения;
- поле пере перемещения;  - поле упругих составляющих
деформации;
- поле упругих составляющих
деформации;
![]() - поле температурных составляющих деформации;
- поле температурных составляющих деформации;
![]() - поле термо-упругих составляющих
деформации;
- поле термо-упругих составляющих
деформации;
![]() - упругих температурных и термо-упругих составляющих деформации.
- упругих температурных и термо-упругих составляющих деформации.
По аналогии поле распределения перемещения ![]() в пределах длины стержня
аппроксимируем полным полиномом второго порядка. Тогда имеем, что
в пределах длины стержня
аппроксимируем полным полиномом второго порядка. Тогда имеем, что
![]()
![]()
(22)
 (23)
(23)
Тога градиент перемещения в пределах длины
стержня определяется по формуле
![]() (24)
(24)
Теперь учитывая по формуле из (21) получим интегрированный вид
потенциальной энергии упругих деформации при наличии поле температуры
 (25)
(25)
Теперь учитывая, что обе концы
рассматриваемого стержня жестко-защемлена то (![]() ) будем минимизировать функционал П только по
) будем минимизировать функционал П только по ![]()
![]() (26)
(26)
Отсюда определим ![]()
![]()
Найденное значение подставляя ![]() в (22) и учитывая, что получим закон распределения перемещения по
длине исследуемого стержня
в (22) и учитывая, что получим закон распределения перемещения по
длине исследуемого стержня
 ( 28)
( 28)
Далее по соответствующиму соотнашению
Каши определяется поле упругой составляющей деформации
![]() (29)
(29)
По
соответствующему закону Гука определяется поле распределения упругой
составляющей напряжения
![]() )
(30)
)
(30)
Исходя
из общих законов термоупругости определяются поле температурных составляющих
деформации и напряжении
[4].
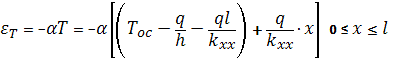 (31)
(31)
 (32)
(32)
Тогда термо-упругие составляющие
деформации и напряжения определяются в соответствии с общим законом Гука
 (33)
(33)
![]() (34)
(34)
Тогда величина возникающего сжимающего
усилия определяет согласно общему закону Гука [4],
следующим образом
![]() (35)
(35)
Теперь эту же задачу прорешим вторым
методом
2-метод решения задачи
Этод
метод основана на пременения условия совмесности деформации.
Для
этого сначало рассмотрим защемленный только левым концом стержень, а правый
свободен( рисунок-3)

Рисунок
3- защемленный левым концом стержень.
Этот стержень, за счет теплового
расширения удленняется на величину
![]() =
=![]()
![]()
Теперь
рассмотрим защемленный левым концом стержень, но сжатой силой R
(рис-4)

Рис-4.
Сжатый стержень.
В
этом случае сжатый стержень укарачивается,на величину ![]() [4].
[4].
![]() (37)
(37)
Если обе конца стержня
жестко-защемлены то она не может удленняться, или укорачивается т.е
![]() =0
(38)
=0
(38)
Отсюда определим R
![]() (39)
(39)
Она
совпадает с (35)
Из
(39) согласно закону Гука можно определить термо-упругую составляющую
напряжения
![]() (40)
(40)
Здесь
(40) совпадает с (34). Соответствующая составляющая деформация определяется
согласно закону Гука ![]() (41)
(41)
Температурное
соcтоавляющее деформации и напряжения определяются
согласно (31-32). Тогда упругие составляющие определяются согласно общему
закону Гука
![]()
(42)
Эта
формула совпадает с (29).
Тогда
упругая составляющая напряжения определяется также согласно закону Гука
![]() (43)
(43)
Это
выражение совпадает с (30)
В
целях иллюстрации данного метода построим графики искомых величин при следующих
искомых данных
![]()
![]()
![]()
![]()
![]() ,
, ![]()
При
этих исходных данных поле распределения температуры,перемещения, составляющие
деформации и напряжения приводятся на рисунках – 4, a-r..
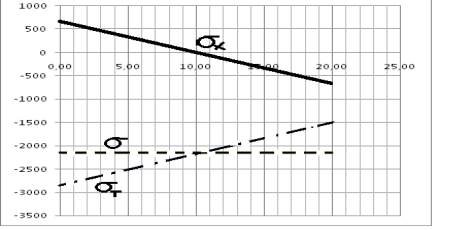
Из
этих рисунков также видно, что поле распределения T(x), имеют линейный характер. В то время поле распределения перемещения
имеют линейный характер. В то время поле распределения перемещения ![]() имеет
нелинейный относительно серединного
сечения стержня имеет симметричный характер. Также
следует отметить что
имеет
нелинейный относительно серединного
сечения стержня имеет симметричный характер. Также
следует отметить что ![]() и
и ![]() постоянна по всей длине стержня.
постоянна по всей длине стержня.
В целях исследования сходимости и
точности полученных решении дискретизированна исследуемый стержень 2,4,8,...100
квадратными элементами. Но во всех случаях были получены одни и те же
результаты. Это еще раз показывает, что полученные аналитические решения
являются точными. Вследствии чего, мы ещё раз убедились, что применения
фундаментальных законов сохранения энергии позволяют решать
любые смешанные задачи с разнородными граничными условиями. При этом полученные
решения всегда будут отличатся большой точностью.
 a)
a)  б)
б)
![]()
 в)
в)
 г)
г)
Риисунок -4. Поле
распределения, перемещения, температуры, составляющих напряжений и деформации.
Литература
1.
Седов
Л.И. Механика сплошных сред. М.1970
2.
Ноздрев
В.Ф. Курс термодинамики. М.1967.
3.
Биргер
И.А. Пановко Я.Г. Прочность, устойчивость колебания. Справка в 3 томах.М:Машиностроение. 1968. 831 с.
4.
Тимощенко
С.П.,Гудьер Дж.Теория упругости. М.Наука. 1979. 560 с.