Технические науки / 6. Электротехника и радиоэлектроника

 

К.т.н. Сухарьков О.В.

Одесская национальная академия связи им. А.С. Попова, Украина

Вынужденные колебания цилиндрической струйной оболочки

 

В информационной гидроакустике особое внимание уделяют проблеме увеличения дальности действия передающей аппаратуры за счет использования более низких частот. Для решения этой проблемы перспективно использовать рупорные антенны, основными элементами которых служат низкочастотные (0,2…5 кГц) жидкоструйные преобразователи [1, 2]. Ранее в качестве модели прямоточного преобразователя были рассмотрены собственные автоколебания затопленной цилиндрической струйной обо­лочки [3]. Целью данного доклада является решение задачи вынужденных колебаний цилиндрической струйной обо­лочки.

             

 

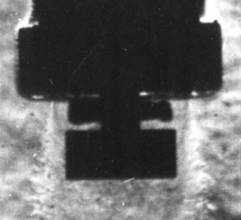
                                а)                                                      б)

 

Рисунок 1 – Прямоточный жидкоструйный преобразователь: а – физическая модель, б – теневая фотография работающего преобразователя

 

Схема прямоточного жидкоструйного преобразователя с кольцевым соплом и ступенчатым препятствием представлена на рис. 1а. Частоту основной гармоники акустического сигнала задает упругая затопленная струйная оболочка 2 цилиндрической формы. Осесимметричная струя вытекает из кругового щелевого сопла 1 и формируется в оболочку ступенчатым препятствием 4. Накопителем энергии является неустойчивый тороидальный вихрь 3 с развитой кавитацией. На теневой фотографии излучателя (рис. 1б)  хорошо видны струйная оболочка и вихрь в форме тороида. Пульсации вихря возбуждают струйную оболочку, которая совершает изгибные колебания. В фазе растяжения свободного нижнего основания оболочки происходит выброс каверн из вихря 3 во внешнюю среду. Частота пульсаций вихря зависит от геометрических параметров преобразователя, гидростатического давления в  окружающей жидкой среде и скорости струи на выходе из сопла. При оптимальном режиме работы преобразователя частота пульсаций вих­ря совпадает с собственной частотой изгибных колебаний струйной оболочки. В этом случае колеблющаяся затопленная струя генерирует тональный звуковой сигнал максимального уровня.

В первом приближении затопленную струйную оболочку можно считать твердотельной с некоторым эквивалентным модулем упругости . Воспользуемся уравнениями динамики вынужденных колебаний для твердотельных оболочек [4]. В случае цилиндрической оболочки параметры Ламе ,  (где  – средний радиус эквивалентного цилиндра), а радиусы кривизны , . Кроме того, при осевой симметрии все упругие величины не зависят от угло­вой координаты . Поскольку оболочка деформируется только в направ­лении нормали к ее поверхности, то сдвигающие усилия и кру­тящие моменты отсутствуют. При этом на любом сечении  также равны нулю изгибающие мо­менты и перерезывающая сила. В связи с тем, что материалом оболочки является жидкость и оболочка, испытывающая колебания, находится в затопленном состоянии в этой же рабочей жидкости, то коэффициент Пуассона [5]. Компоненты удельных внешних усилий в направлении оси симметрии , окружной оси  и нормали принимают соответственно следующие значения:

                                                  ,                                   (1)

где  – параметр времени;  – круговая частота. Предполагаем, что оболочка деформируется под действием сил, равномерно распределенных по ее внутренней поверхности, и потому совер­шает только изгибные гармонические колебания. С учетом этих допущений после преобразования системы уравнений движения оболочки [4] оставим только те уравнения, в которые входит интересующее нас изгибное смещение . Тогда система уравнений движения оболочки принимает вид [6]

             

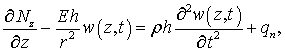
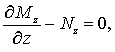
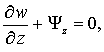
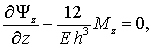                                                            (2)

где  – плотность материала, радиус средней поверхности, длина и толщина струйной оболочки (рис. 1а);  – модуль объемной упругости жидкости;  – осевая координата;  – окружная координата;  – нормаль к элементу поверхности;  – угол между касательной к окружной оси и нормалью в точках на поверхности цилиндра. На элемент оболочки действуют удельное перерезывающие усилие  и удельный изгибающий момент .

Согласно физической модели преобразователя [3] на защемленном основании оболочки  отсутствует смещения, а на свободном – равны нулю перерезывающие усилия и изгибные моменты. Поэтому граничные условия на основаниях оболочки имеют вид

                                                                 (3)

Используя методику работы [6], с учетом выражений (1), систему уравнений (2) можно свести к одному  уравнению:

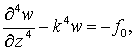                                                                                                     (4)

                                                                             (5)

где  – характеристическое волновое число оболочки;  – амплитуда удельной возбуждающей силы со стороны тороидального вихря, которая равномерно распределена по внутренней поверхности оболочки. Модуль упругости  струйной оболочки можно выразить через адиабатический модуль объемной упругости жидкости  [5]:

                                                                         (6)

где – предел прочности жидкости на разрыв;  – избыточное (по сравнению с атмосферным давлением) статическое давление на глубине моря;  – коэффициенты, кото­рые практически не изменяются в широком диапазоне температур жидкости, но зависят от объема включений (мелкодис­персные твердые частицы, растворенный газ, зародыши кавитационных пузырьков и др.).

Общее решение неоднородного уравнения (4) имеет вид [6]

               .       (7)

Неизвестные коэффициенты , ,  и  найдем, подставив выражение (7) в граничные условия (3). Тогда для функции изгибных колебаний  получим

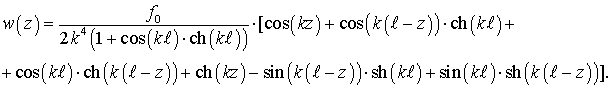 (8)

Выражение (8) позволяет определить формулы (9) и (10) для расчета амплитуды вынужденных изгибных колебаний свободного края оболочки :

                                         .                                    (9)

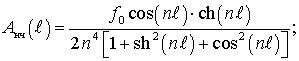
                 .        (10)

Функцией (9) можно пользоваться в интервале частот выше резонансной частоты, а функцией (10) – в интервале частот ниже резонансной частоты.

В заключение отметим, что решение задачи вынужденных колебаний цилиндрической струйной оболочки позволяет рассчитывать на стадии проектирования амплитудно-частотные характеристики (АЧХ) прямоточных жидкоструйных преобразователей. Для струйных оболочек средней длины, в этом случае реальные преобразователи генерируют звуковые волны максимальной интенсивности, расхождение между теоретической зависимостью АЧХ и данными эксперимента не превышает 5 %.

 

Литература:

 

1.      Сухарьков О.В. Гидроакустическая излучающая рупорная антенна на основе  жидкоструйного преобразователя / О.В. Сухарьков // Акустичний вісник. – 2011. – 14, № 1. – С. 56 – 63.

2.      Сухарьков О.В. Передача дискретной информации в гидроакустический канал связи с использованием жидкоструйных преобразователей / О.В. Сухарьков // Цифрові технології. – 2011. – № 9. – С. 100 – 110.

3.      Дудзінський Ю.М. Модель прямоточного гідродинамічного випромінювача з кільцевим соплом і східчастою перешкодою / Ю.М. Дудзінський, О.В. Сухарьков, Н.В. Манічева // Акустичний вісник. – 2004. – 7, № 3. – С. 49 – 54.

4.      Огибалов П.М. Оболочки и пластины / П.М. Огибалов, М.А. Колтунов. – М.: Изд-во МГУ, 1969 . – 695 с.

5.      Корнфельд М. Упругость и прочность жидкостей / М. Корнфельд. – М.: ГТТИ, 1951. – 200 с.

6.      Дудзінський Ю.М. Спектр звуку, генерованого зануреною осесиметричною струминною оболонкою / Ю.М. Дудзінський, О.В. Сухарьков // Математичні методи та фізико-механічні поля. – 2007. – 50, № 2. – С. 129 – 134.