к.т.н. Лимаренко О.М., Дубчак О.О., Мелиш В.Ю.

Одеський національний політехнічний університет

напружений стан ЦИЛІНДРА ПРЕСУ моделі Д-0843

Необхідність проведення перевірочного розрахунку міцності циліндра зумовлена тим, що останнім часом головний циліндр преса моделі Д-0843 зазнав конструктивних змін. Форма головного циліндра преса достатньо складна (рис.1, а). Внутрішній тиск в циліндрі при випробуванні 40 МПа, а навантаження осьовими силами в місцях кріплення циліндра з колонами преса взяте рівномірно розподіленим по довжині чотирьох бокових кронштейнів. В період розробки проектів попередніх моделей не існувало достатньо надійної та чіткої методики розрахунку тривимірних деталей, тому користувались методами, що давали можливість визначати напруження в елементах конструкції дуже приблизно [1]. Крім цього, матеріал циліндра сталь 35Л має невисокі механічні характеристики, і тому з врахуванням недостатньої якості виготовлення таких товстостінних деталей допустимі напруження приймались достатньо низькими.

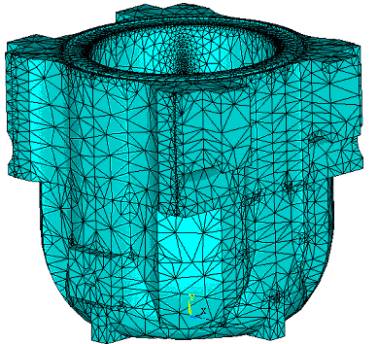
Рис. 1.  Модель головного циліндра преса Д-0843 з скінченно-елементною сіткою

Розглянувши різні методи дослідження напружено-деформованого стану масивних тіл, у тому числі –– шляхом лабораторних дорогих випробувань в поляризованому світлі, зроблено висновок, що розрахунок на міцність головного циліндра слід виконувати методом скінченних елементів. На основі цього для дослідження напружено – деформованого стану елементів потужних гідропресів використано програмний пакет ANSYS [2].

Для оцінки достовірності результатів, отриманих на ЕОМ, було визначено напруження в елементах схематизованого ідеального циліндра за допомогою відомих формул теорії пружності [3]. В таких розрахунках циліндр вважається тілом обертання без кронштейнів, отворів, опор. В нижній частині циліндр сполучається з днищем як з круглою пластиною, яка вважається жорстко закріпленою на контурі, радіальний з округленням перехід від стінки циліндра до днища не враховується.

Для визначення напружень у стінці циліндра Д-0843 з використанням формули Ляме [3] взято такі вихідні дані: радіус внутрішньої поверхні циліндра м; радіус зовнішньої поверхні циліндра м; внутрішній тиск рідини взято одиничним, безрозмірним (), щоб всі напруження були в долях цієї одиниці.

Розрахункові формули і величина одиничних напружень на внутрішній поверхні стінки циліндра (рис. 2):

Рис. 2. Напружений стан елемента товстостінного циліндра

радіальне нормальне напруження

                                                

колове нормальне напруження в напрямі дотичної до циліндричної поверхні

                                                 

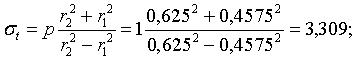
нормальне напруження в поперечному перерізі з площиною А зумовлене поздовжньою силою N

                   

еквівалентне напруження за четвертою, енергетичною теорією міцності

                       σекв

       σекв .      

Днище циліндра розглядаємо, як круглу пластину, жорстко затиснену на контурі і навантажену рівномірним одиничним безрозмірним тиском.

Вихідні дані для визначення напружень: =0,4575 м –– радіус пластини, h = 0,22 м –– товщина пластини.

Згинальний момент радіальний в кільцевих перетинах

                                    

де  r – поточний радіус-вектор точки в круглій пластині;

μ – коефіцієнт Пуассона;

згинальний коловий момент в радіальних перетинах

                                                                          

Для довгої оболонки з днищем при =0,333 маємо:

                                  

                                    

В центрі пластини відносні (одиничні) згинальні моменти і напруження будуть такі

                              ;

                            

Еквівалентне напруження згідно з енергетичною гіпотезою

                                   σекв                                   

Для дослідження напружено-деформованого стану циліндра Д-0843 з використанням кінцево-елементного пакета „ANSYS“ використовувались вихідні дані: матеріал циліндра – сталь 35Л ГОСТ 977-88, для якої границя текучості σт = 250 МПа,  границя міцності σв = 470 МПа, модуль поздовжньої пружності МПа, робочий тиск Рроб = 32 МПа, випробувальний тиск Рвипр = 40 МПа, максимальне зусилля преса 27000 кН.

Для розв’язання задачі числовим методом спочатку необхідно побудувати геометричну модель деталі, для цього ANSYS має засоби тривимірного моделювання. Тіло складного за окресленням циліндра було поділене більш ніж на п’ять тисяч об’ємних елементів з відповідною кількістю (більше 50 тисяч) вузлів.

Результати рішення включають значення переміщень, напружень, деформацій і ви в графічній і табличній формах. На епюрах еквівалентних напружень ординати показують їх величину у відповідних вузлах, а цифрами позначені найбільші напруження в небезпечних точках конструктивних елементів циліндра (рис. 3).

Рис. 3. Епюри еквівалентних напружень в поздовжньому розрізі циліндра

Результати визначення еквівалентних напружень в небезпечних точках характерних перерізів циліндра методами теорії пружності та з використанням програмного комплексу ANSYS наводяться (таблиця 1). Розрахунки виконані для одиничного тиску  (р =1).

 

Порівняння чисельних результатів розрахунку в програмах ПРИЗМА, АNSYS та методами теорії пружності

№

п/п

Характерні перерізи і

точки циліндра

Еквівалентні напруження в небезпечних точках

ANSYS

Теорія пружності

1

Поперечний переріз циліндричної частини

2,92

2,84

2

В центрі внутрішньої поверхні днища

2,19

2,16

3

В центрі зовнішньої поверхні днища

2,88

2,86

4

Біля отвору на внутрішній поверхні циліндра

3,9

––

5

На галтелі з’єднання циліндра з днищем

3,41

––

 

Аналіз напружень, отриманих у результаті розрахунків, дозволяє зробити такі висновки. Спостерігається нерівномірність розподілу напружень по висоті циліндра і по днищу. Найбільші напруження виникають в зонах дії зусиль, прикладених до кронштейнів, в місцях різкої зміни форми та в центрі днища. Розрахований по границі текучості матеріалу циліндра фактичний коефіцієнт запасу міцності в найбільш напруженому місці (біля отвору) nф  під випробувальним тиском.

Епюри розподілу напружень в перерізах елементів циліндра, визначених за допомогою програмного комплексу, адекватні за характером, так що кінцево-елементний комплекс ANSYS правомірний при дослідженні напружено-деформованого стану масивних тіл складної конструкції.

 

Література

1.   Расчет и конструирование базовых деталей гидравлических прессов. –– Воронеж: ЭНИКМАШ, 1972. –– 72 с.

2.  Чигарев А.В., ANSYS для инженеров. Справочное пособие. / Чигарев А.В., Кравчук А.С., Смалюк А.Ф. –– М.: Машиностроение, 2004. –– 511с.

3.   Писаренко Г.С. Опір матеріалів: Підруч. / Писаренко Г.С., Квітка О.Л., Уманський Е.С.; за ред. Г.С. Писаренка. –– К.: Вища шк., 1993 –– 654.