Економіко-математичні моделі в дослідженнях

Розвиток економічних наук потребує не тільки нових теоретико-методологічних зрушень, а й постійних статистичних та математичних досліджень. Одним із сучасних методів математичних досліджень є математичне моделювання. Вперше математичні моделі були використані на практиці в 30-х роках в Великобританії в розробці системи протиракетного захисту. З цього моменту вчені застосовують термін «операційне дослідження», який зазнав подальшого розвитку не тільки в військовій сфері. 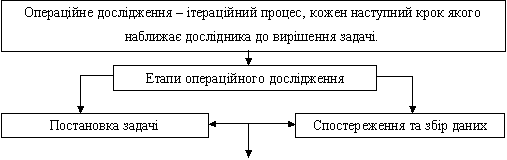Згодом операційні дослідження розвиваються як окрема наука та дають змогу отримати оптимальне рішення при управлінні реальними процесами та системами. Етапи операційного дослідження представлені на рис. 1.

Побудова математичної моделі

Рис. 1. Етапи операційного дослідження

Основою операційного дослідження в фінансах є математична модель. Вона є системою математичних співвідношень, наближено, в абстрактній формі, які описують досліджуваний процес чи систему.

При одержанні математичної моделі використовують загальні закони природознавства, спеціальні закони конкретних наук, результати пасивних та активних експериментів, імітаційне моделювання за допомогою ЕОМ. Математичні моделі дозволяють передбачити хід процесу, розрахувати цільову функцію (вихідні параметри процесу), керувати процесом, проектувати системи з бажаними характеристиками.

Для створення математичних моделей в економічних науках можна використовувати будь які математичні засоби — мову диференційних або інтегральних рівнянь, теорії множин

, абстрактної алгебри

, математичну логіку

, теорії ймовірностей

, графи

та інші. Процес створення математичної моделі називається математичним моделюванням

.

В економічних науках для досліджень використовуються економіко-математичні моделі. Застосування економіко-математичних моделей дає змогу проаналізувати економічну ситуації та обрати оптимальні рішення щодо управління нею або описати запропоновані рішення. Застосування таких моделей необхідне в тих випадках, коли проблема є складною та потребує розгляду багатьох факторів для прийняття рішень. Опираючись на модель можна зробити оптимальні (або близькі до них) висновки за конкретними критеріями. Слід зауважити, що не існує повністю оптимальних рішень. Будь-яке рішення, отримане з використанням економіко-математичної моделі, оптимальне по одному або декільком критеріям, які є вхідними даними.

Сьогодні економіко-математичні моделі застосовуються для аналізу, прогнозування та прийняття оптимальних рішень в різних галузях економіки. Це планування та оперативне управління виробництвом, управління трудовими ресурсами, управління запасами, розподіл ресурсів, розподіл інвестицій та ін.

Загальна класифікація економіко-математичних моделей охоплює понад десять основних ознак. З розвитком економіко-математичних досліджень проблема класифікації застосовуваних моделей дедалі ускладнюється. Поряд з появою нових типів моделей (особливо мішаних типів) і нових ознак їх класифікації відбувається інтеграція моделей різних типів у складніші модельні конструкції.