д.б.н., проф., Колесник Ю.А., к.б.н., с.н.с. Тимофеева А.А.
Дальневосточный федеральный университет (филиал в г. Уссурийск),
Россия
Многолетние
изменения склонения Луны и его следствие для Земли
Одним из факторов, оказывающим огромное
воздействие на климатические системы нашей планеты, является периодические
колебания склонения Луны. Известно, что при среднем его значении 23027,
оно изменяется в пределах от 18019` до 28035 и более (и
обратно) (Максимов и др.,1970). Период этих смещений 18,6-19 лет. Аналогичные
периоды обнаружены в других явлениях, которые не проходят бесследно для нашей
планеты. Это нутация земной оси (Куликов, 1985, С.60-61, Рябов, 1988, С.
154-155), многолетний лунный и полюсный приливы (Багров с соавт., 1985, С.
60-62) изменение ротационного режима планеты и т.д.. Исследования
свидетельствуют, что через ряд промежуточных возмущений среды, биота, также
реагирует на их воздействие (Саблин, 1980, С.91-98; Тимофеева, Колесник, 1998, Parker, Royer, Deriso, 1995, p.p 447-459).
Нутации (как и прецессия) вызываются Луной
и Солнцем, которые приводят к вынужденным колебаниям земной оси. Эти колебания
имеют различные периоды. Наибольшее колебание вызывается изменением наклона орбиты
Луны к земному экватору. Данное изменение связано с попятным движением линии
узлов лунной орбиты, поэтому основной период равен 18,6 года, т.е. периоду
оборота линии узлов. Полное освещение искомого механизма можно найти в
специальных публикациях (Куликов, 1985, С.56-57, Жаров, 2009, ресурс Интернет и
др.). Отметим, что если бы Солнце и Луна находились в плоскости экватора, то
регистрируемых нарушений ротационного режима планеты не наблюдалось, так как
сила притяжения нашим спутником проходила бы через центр планеты.
Следовательно, можно уже априори утверждать, что изменение склонение Луны
должно влиять на вращение нашей планеты. Каким образом? Один из сценариев
решения поставленной задачи был опубликован нами ранее (Колесник, 2002,
С.1275-1297; 2006, C:139-141).
Почему скорость движения Луны по орбите,
согласно расчетам (Рябов, 1988), равна 1,02 км/с? Мы считаем, что искомая
закономерность является не случайной. Приравняем центробежную силу силе
взаимного тяготения, т.е.
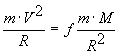 (1),
(1),
где - m, V, M, f, R, соответственно масса Луны (7,34*1022 кг), ее скорость по орбите, масса Земли (5,976 1024 кг),
гравитационная постоянная (6,672 10-11
м3/ кг с2), и расстояние от центра Луны до центра
Земли (R=384400 км.)
Преобразовывая (1) определим скорость
движения Луны по орбите. Имеем,
![]() ,
(2).
,
(2).
Как следует из (2) при увеличении
расстояния Луны до Земли, ее скорость уменьшится, а это приведет, согласно
правой части (1) к ослаблению сил тяготения. В конечном итоге спутник должен
уйти с орбиты. Обратно, при уменьшении расстояния, силы взаимного тяготения
должны возрастать, что приведет к катастрофическому сближению Луны с Землей.
Таким образом, скорость Луны по орбите
является оптимальной для устойчивого состояния двух взаимодействующих систем,
т.е. Земля-Спутник.
Можно определить показатель V по формуле, вида
V=ώR
(3)
где ώ - угловая скорость обращение Луны вокруг
Земли. Она равна 2π/27,3 86400=0,0000027,
V=0, 0000027 384400=1, 02 км/с
В соответствии с (2)
определим скорость обращения (Vз)
материального тела на поверхности Земли, например у экватора. Имеем,
Vз = Wrcosφ,
(4),
где W, r и φ соответственно, угловая скорость вращения
Земли (7,3∙10-5,
), радиус Земли (r=6370 км) и – географическая широта. Так как на экваторе
φ=0, то
Vз=7,3∙10-5
6370км=0,465км/с
Таким образом, скорость
движение Луны в 2 раза превышает линейную скорость точек на широте экватора.
Это важный факт для понимания роли Луны в земных процессах. Допустим, что Луна
находится в экваториальной плоскости Земли. Соединив их центры прямой ОХ,
определим центр масс по формуле,
Хс=![]() (5).
(5).
В этой точке Земля и
Луна уравновешивают друг друга. Это следует из закона рычага (Зельдович, 1968),
![]() , или,
, или,
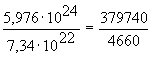 , или,
, или,
M∙Xc=(R-Xc)∙m. (6).
Как следует из левой и
правой части (6) размерность каждой из них кгм, что в технической системе единиц
является измерением работы (Зельдович, 1968, С. 348-349). Отсюда вытекает интересный
вывод.
Земля за счет сил
тяготения пытается сместить центр масс к своему центру, т.е. совершает работу,
а Луна, за счет сил всемирного тяготения производит обратное действие.
Результат этой борьбы сил - установившееся равновесие, точкой которого является
центр масс. Однако Луна изменяет свое (по отношению к плоскости земного
экватора) положение. Следовательно, центр масс, также будет смещаться в
долготном направлении, например, к полюсу планеты. Известно (Шебалин, 1981, С.
44-45), что под действием внешних сил (F), приложенных к системе, ее центр масс движется как
материальная точка, в которой сосредоточена вся масса системы. Результат данной
закономерности уменьшение углового момента вращения центра масс, за счет его
смещения ближе к оси вращения Земли, а, следовательно, к нарушению равенства
(6).
Скорость перемещения
центра масс будет равна сумме скоростей за счет вращения Земли (Vз) и Луны (Vл), т.е.
V=Vз + Vл. Когда смещение Луны будет направлено (по отношению
к плоскости земного экватора) к высоким широтам планеты, то радиус вращения
центра масс вокруг земной оси должен уменьшиться.
Учитывая (4), определим
угловую скорость вращения Земли, как
![]()
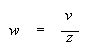 (7).
(7).
где ![]() -скорость движения центра масс, AB=z смещенное
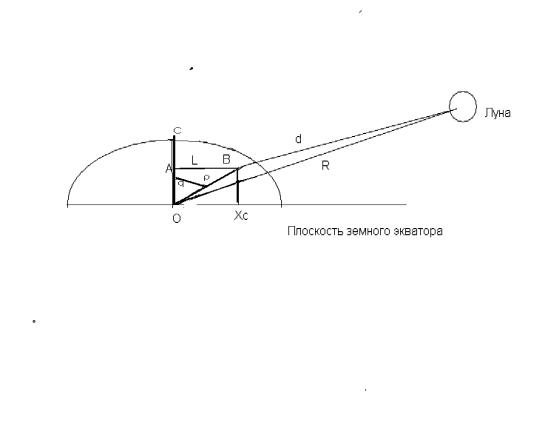
расстояние центра масс до оси вращения Земли (ОС) (см. рис)..
-скорость движения центра масс, AB=z смещенное
расстояние центра масс до оси вращения Земли (ОС) (см. рис)..
Следующие обозначение OB= ρ характеризует расстояние от центра Земли, до
смещенного положения центра масс. OA=Y-Расстояние от центра Земли по до точки пересечение
центра масс оси вращения планеты. Примем, для простоты исчислений, что Земля
имеет шарообразную форму, и, сделаем по широте мысленный поперечный разрез
(см.рис.). На нем приведена схема положения центра масс (Xc), обусловленная склонением Луны. Из треугольника OAB определим z, т.е. расстояние от центра масс до оси вращения
Земли. Заметим, что искомое расстояние можно определить как z=r sinq, но для более глубокого анализа мы приняли во
внимание теорему косинусов, вида;
Z2= ρ2+Y2-2ρYcosq (8).
Подставляя (8) в (7), после ряда преобразований, имеем
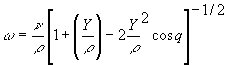 (9).
(9).
Выражение,
представленное в квадратных скобках (см. 9), является полиномом Лежандра
(сферические многочлены, Мантуров с соавт.,1978, С. 293). Разложив их в ряд, по степеням ![]() определим полиномы
Лежандра от cosq, т.е P0=1; P1=cosq; P2=
определим полиномы
Лежандра от cosq, т.е P0=1; P1=cosq; P2=![]() ; P3=
; P3=![]()
![]()
![]() ); P4=
); P4=![]() и т.д. (Несис, 1977, С.143-148; Мантуров с соавт, 1978, С.
293).
и т.д. (Несис, 1977, С.143-148; Мантуров с соавт, 1978, С.
293).
Подставляя (8) в (7), после ряда преобразований,
получим
 (9).
(9).
Выражение, представленное
в квадратных скобках (см. 9), является полиномом Лежандра. Проделав еще ряд
преобразований и исчислений получим следующее выражение для (7).
w=w0+w1+w2+w3+…
=![]() (10).
(10).
Прокомментируем (10).
Поскольку w0 =![]() =const, то это
значит, что угловая скорость Земли постоянна и она не подвержена влиянию Луны.
Точнее,
=const, то это
значит, что угловая скорость Земли постоянна и она не подвержена влиянию Луны.
Точнее, ![]() w0 =const. Следующий
показатель
w0 =const. Следующий
показатель
w1 = ![]()
![]() const (11).
const (11).
В
соответствии с (3) и учитывая, что Y имеет
размерность расстояния (z, где числитель
T-1 L2 , а знаменатель L2),
проведенной от смещенного центра масс к оси вращения Земли (см. рис.) то w1= ![]() . Следовательно, угловая скорость вращения планеты зависит от
широты. Это общеизвестная закономерность.
. Следовательно, угловая скорость вращения планеты зависит от
широты. Это общеизвестная закономерность.
Таким
образом, два члена ряда не оказывают значительного влияния на ротационный режим
планеты, что нельзя сказать о следующих показателях. Изучение этой проблемы
свидетельствует, что кроме многолетнего лунного прилива (период 18.6-19 лет)
миграции долгопериодных перемещений центра масс, вызванные изменениями
склонения Луны не должны проходить бесследно для динамики нашей планеты, а
следовательно и для вибраций климатических систем. Действительно, по мере
изменения склонения Луны, общий центр масс будет, также синхронно изменять свое
положения для того чтобы оставаться на оси ОХ (на рис. прямая центров
Земля-Луна. В соответствии с этой закономерность, центр масс буде подниматься
по отношению к оси вращения по правилу правого винта, если смотреть из центра
Земли. Следовательно, чтобы выполнялось условие (6) ось планеты должна
отклонится на заданную величину, а это уже феномен нутации. Как это происходит
нами будет показано в последующих публикациях.
Литература
Багров Н.А., Кондратович Д.А., Педь А.И. Долгосрочные метеорологические
прогнозы. Л.: Гидрометиздат, 1985. 243 с.
Зельдович Я.Б Высшая
математика для начинающих. - М.:, Наука, 1968. 575с.
Колесник Ю.А. Неравномерность
вращения Земли и ее влияние на природные процессы, и динамику биосистем //Изв.
ТИНРО.-2002.-Т.130, ч.111.-С.1283-1297.
Колесник Ю.А.,
Сценарий долгопериодных изменений скорости вращения Земли: //Фундаментальные
исследования в технических университетах, материалы Х Всероссийской конференции
по проблемам науки и высшей школы, Санкт-Петербург, 2006, 139-141 (0,2).
Куликов К.А. Вращение Земли. М.:
Недра, 1985, .-156с.
Максимов И.В., Э.И. Саруханян,
Н.П. Смирнов. Океан и Космос.Л.: Гидрометиздат, 1970.-214с.
Мантуров О.В., Солнцев Ю.К., Соркин Ю.И., Федин Н.Г. Математика в понятиях, определениях и терминах (часть 1), М. Просвещение, 1978, 319с.
Несис Е.И. Методы
математической физики. М. Просвещение, 1977, 192с.
Рябов Ю.А.
Движение небесных тел. М.: Наука, 1988. 237 с.
Саблин В.В.
Воспроизводство и динамика численности сайры в северо-западной части Тихого
океана. Автореф. дис. ... канд. биол. наук. Севастополь, 1980. 23 с.
Тимофеева А.А.,
Колесник Ю.А. Эти удивительные котики. Владивосток, Изд. ДВГУ, 1998, 100с.
Шебалин О.Д. Физические основы механики и
акустики. М.: Высшая школа, 1981. 260 с.
Parker K.S., Royer T.C., Deriso R.B. High-latitude
climate forcing and tidal mixing by the 18.6-year lunar nodal cycle and
lowfrequency recruitment trends in Pacific halibut (Hippoglossus stenolepis)// Сlimate
change and Northern fish populations.1995 Can. Spes. Publ. Fish. - Hational
Research Council of Canada – Ottawa - pp. 447-459.