МОДЕЛИРОВАНИЕ ПАРАЛЛЕЛЬНОГО КАНАЛА СВЯЗИ ДЛЯ ПЕРЕДАЧИ ДАННЫХ В ПАРАЛЛЕЛЬНОМ ФОРМАТЕ

Чемерисов А.Ю., Смирнов А.А., Набродов П.А.

Аннотация. В статье проведено моделирование параллельных каналов связи с применением оборудования генерации и анализа сигналов произвольной формы с несколькими подканалами. В основе параллельного представления сигнала использовалась система остаточных классов.

Параллелизм является основным направлением развития средств передачи данных, поскольку позволяет максимально повысить как помехоустойчивость, так и скорость передачи данных. Наиболее перспективным способом наращивания пропускной способности КС является использование параллелизма при построении информационных сетей [1-3], т.е. передача информации по нескольким каналам одновременно. Известно, что максимальная эффективность указанных технологий достигается при использовании параллельной математики в обработке сигналов, такой как система остаточных классов (СОК), алгебраические операции в которой осуществляются параллельно.

Таким образом целью статьи является проведение натурного эксперимента с использованием оборудования анализа и генерации сигналов произвольной формы. Данное оборудование имеет возможность подключения к ЭВМ.

При обработке и передаче данных в телекоммуникациях целесообразно использовать в качестве оснований СОК числа Мерсена () [5], поскольку они максимально близки к форматам последовательной передачи параллельных данных, что позволяет адаптировать существующую систему последовательной передачи данных к параллельной, такой как CDMA и др. Основное преимущество заключается в том, что не только формат или модуляция является параллельной, но и данные представлены в параллельном формате. Это позволяет прежде всего формировать отдельные подканалы по отдельному каналу, кроме того перераспределять спектр КС по отдельным подканалам в зависимости от изменения помехоустойчивости общего канала связи.

В рамках задачи исследования был проведен эксперимент с использованием следующего оборудования: двухканальный генератор сигналов произвольной формы (Актаком – 4106), генератор Гауссовского шума с измеряемыми параметрами и двухканальным запоминающим осциллографом (PCSU1000) с USB интерфейсом версии 2.0. В качестве экспериментального сигнала для исследования указанных выше параметров параллельного КС при передаче данных в формате СОК был использован сигнал в формате ПСС при последовательной передаче (1101). Данный сигнал при минимальной длительности имеет максимальную автокорреляционную функцию (АКФ). В качестве оснований СОК для представления последовательного сигнала были выбраны [4] числа Мерсена 3 и 7, что перекрывает диапазон представления сигналов в ПСС (3*7=21). Перевод сигнала из ПСС в СОК представлен на рисунке 1.

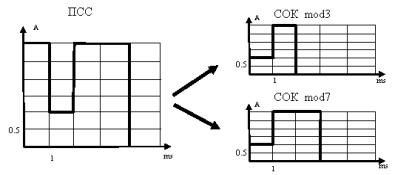
Рисунок 1 – Перевод последовательного двоичного сигнала из ПСС в 2 параллельных сигнала в СОК по основаниям 3 и 7

Из рисунка 1 видно, что суммарная длительность сигнала в СОК больше чем сигнала в ПСС. Однако по аналогии с импульсно – кодовой модуляцией каждый отдельный подканал в СОК несет в себе часть информации об исходном сигнале. Если трансформировать данную схему на множество каналов, то утрата одного из подканалов влечет лишь снижение точности восстановленного сигнала в ПСС. Как было сказано ранее остается открытым вопрос показателей качества параллельного КС при передаче данных в СОК. На данном примере исследуем влияние аддитивной помехи в каждом подканале на общую помехоустойчивость параллельного КС.

На рисунке 2 представлена аддитивная смесь последовательного и двух параллельных сигналов с динамическим диапазоном (А) 2.5V и среднеквадратическим отклонением шума 0.5V. Т.к. длительность сигнала в первом подканале уменьшается в 2 раза, а во втором подканале в 2/3 раза, то эпюры указанных сигналов были приведены в соответствующих частотных диапазонах.

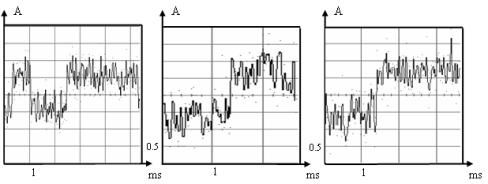
Рисунок 2 – Аддитивная смесь сигналов в ПСС и СОК и гауссовского шума

Для расчета статистических характеристик, отношения сигнал/шум и др. были использованы стандартные программные средства оборудования. При этом учитывался частотный диапазон передачи элементарного импульса.

Ниже, на рисунке 3 представлены результаты исследования в частотных диапазонах до 1МГц. Проведен экспериментальный анализ одного из показателей качества (отношение сигнал/шум) параллельного канала при передаче данных в формате СОК на различных частотах. Для сбора статистики использовано более 3000 измерений.

Рисунок 3 – Изменение отношения сигнал/шум от частоты (- - - экспериментальные данные, –––– характеристика канала)

Из рисунка 3 видно, что отношение сигнал/шум лучше на двух параллельных каналах, чем на одном последовательном, что логично, т.к. при передаче по двум каналам параллельно сигнал получается менее уплотненным и межсимвольная интерференция на нем сказывается меньше. При повышении рабочей частоты КС отношение сигнал/шум ухудшается на всех каналах, но при этом на параллельных каналах связи регресс заметно ниже. При этом на рисунке 3 отчетливо видна полоса повышения качества сигнала при изменении частоты сигнала на промежутке от 100Гц до 1кГц, этот эффект может быть следствием ТТХ канала связи [4, 5].

Можно сделать вывод, что параллельная передача параллельных данных наиболее эффективна, обладает рядом преимуществ и может быть реализована ни только в 4G, но и в других перспективных форматах параллельной передачи данных. Преимуществом применения параллелизма является повышение помехоустойчивости не только при воздействии аддитивных, но и мультипликативных помех.

СПИСОК ЛИТЕРАТУРЫ

1. Кловский Д. Д. Теория электрической связи. - М.: Радио и связь, 1999. - 304 с.

2. Комашинский В.И. Нейронные сети и их применение в системах управления и связи / В.И. Комашинский, Д. А. Смирнов – М.: Телеком, 2002. – 94 с.

3.Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение, 2-е издание. – М.: Вильямс, 2003. –1104 с.

4.Смирнов А.А. Моделирование и исследование цифрового согласованного фильтра в нейронной сети с обратным распространением ошибки / А.А. Смирнов, А.С. Смирнов, С.В. Косторнова, Е.Н. Штрекер // Нейрокомпьютеры, разработка и применение. – М.: Радиотехника, 2009. – 80 с.

5. Смирнов А.А., Чемерисов А.Ю., Набродов П.А. Современное Состояние и приоритеты развития фундаментальных и прикладных исследований в области физики, математики и компьютерных наук: Материалы 56-й НМК «Университетская наука – региону». Ставрополь: ИИЦ «Фабула», 2011. – 198 с.