Горская И.Ю, Кузнецов С.С.

Таврический Национальный Университет им. В.И. Вернадского

Оптимизация геометрических параметров многополюсной магнитной линзы

 

В настоящее время постоянные магниты широко применяются в различных областях техники, таких как автомобилестроение, ускорительная техника, авиация, бытовая электротехника и т.д. В связи с этим весьма актуальной остаётся проблема эффективного использования магнитотвёрдого материала при проектировании и конструировании устройств различного назначения.

На кафедре прикладной электродинамики Таврического национального университета весьма успешно в течении ряда лет ведутся исследования по расчёту и оптимизации систем с постоянными магнитами. Настоящая работа является продолжением этих исследований и посвящена оптимизации геометрических параметров мультиполюсной магнитной линзы по критерию максимума модуля поля индукции на рабочей поверхности. Такое требование к распределению поля предъявляется, например, в фокусирующих устройствах ускорительной техники при транспортировке заряженных частиц. Линзы традиционной конструкции с явно выраженными полюсами /1/ относительно сложны в изготовлении, так как содержат постоянные магниты в виде блоков, магнитомягкое ярмо, окружающее эти блоки снаружи, и, как правило, полюсные наконечники со специальным профилем, формирующие магнитные потоки для образования в рабочей области необходимого рабочего мультипольного поля. Кроме того, в указанных линзах пространство вне рабочей области между смежными магнитными блоками и ярмом оказывается бесполезным и в нём образуется рассеянное поле, что обуславливает невысокую эффективность использования магнитного материала.

Расчёт и оптимизацию магнитной системы будем проводить для линзы которая выполнена из 2N (N полюсных и N межполюсных) участков, где N – число полюсов линзы. Полюсные и межполюсные участки выполнены из магнитотвёрдого материала, имеющего намагниченность J. Сечения всех участков представляют собой трапеции. Внутренняя граница линзы в сечении имеет вид многоугольника, имеющего 2N сторон и касательного к окружности радиуса R1, причём магнитная линза может касаться окружности внутренними границами полюсных и межполюсных участков. Полюсные и межполюсные участки намагничены однонаправлено; оси лёгкого намагничивания полюсных участков параллельны осям соответствующих полюсов; оси лёгкого намагничивания межполюсных участков перпендикулярны соответствующим нейтралям. Внешняя граница линзы также представляет из себя многоугольник с 2N сторонами, вписанный в окружность радиуса R2.

Требуется определить оптимальные значения геометрических параметров полюсных и межполюсных участков, обеспечивающих создание магнитного поля с максимальным значением модуля поля индукции на поверхности рабочей области радиуса R­0.

Расчёт магнитного поля линзы проводился при следующих предположениях: во-первых, распределение вектора намагниченности мультиполюсной магнитной линзы плоскопараллельное; во-вторых, магнитная линза бесконечно длинная вдоль оси z; в-третьих, линза во всех точках намагничена однородно, до насыщения, при этом J=const, то есть линза выполнена из материала, намагниченность которого не зависит от величины внешнего поля.

Для расчёта поля постоянных магнитов будем использовать зарядовую модель, в соответствие с которой поле постоянного магнита, намагниченного однородно, можно рассчитывать по формуле:

 

,

 

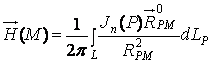где L – кривая, в сечении ограничивающая поверхность всех участков линзы; P – точка принадлежащая кривой L; M – произвольная точка пространства;  - расстояние между точками P и M;  - единичный вектор радиус-вектора ; Jn(P) – нормальная компонента  на поверхности магнита.

Оптимизацию геометрических параметров будем производить при определенных значениях радиусов R1 и R2 для конкретных магнитотвёрдых материалов с заданными значениями остаточной индукции. Процесс оптимизации магнитной системы предполагает проведение серии прямых расчётов магнитного поля для различных геометрических параметров мультиполюсной линзы и выбор оптимальных значений этих параметров, обеспечивающих создание на поверхности рабочей области поля с максимальным значением модуля магнитной индукции. Кроме того, в данном случае появляется возможность варьировать различные магнитотвёрдые материалы, подбирая их по требуемому значению поля в рабочей области и исходя из наличия того или иного материала.

         Указанный подход  к оптимизации устройств, то есть расчёт большого числа различных вариантов конструкции и выбор из них наилучшего варианта по какому-либо критерию, называется эволюционной оптимизацией.

По описанному выше алгоритму была проведена оптимизация магнитной системы мультиполюсной линзы. Расчёты показали, что для различных значений радиуса окружности, описывающей сечение магнитной линзы, при любом числе полюсов N, при условии, что линза выполнена из одного материала, максимум поля индукции на поверхности рабочей области достигается в том случае, если линза выполнена из участков одинаковой формы и размеров. Как показали расчеты, максимальное абсолютное отклонение в распределении модуля поля индукции от его среднего значения для оптимизированных конструкций составляет не более 4%.

Разработанный алгоритм оптимизации был также использован для конструкций многополюсных линз, у которых полюсные и межполюсные участки изготовлены из различных магнитотвёрдых материалов. Размеры полюсных и межполюсных участков в этом случае, как и следовало ожидать, получились различными.

         По результатам расчёта для используемых магнитотвёрдых материалов можно выбрать, по требуемому значению магнитного поля в рабочей области, линзу с минимальными массогабаритными характеристиками.

Предлагаемая методика и пакет прикладных программ может быть использован при проектировании и конструировании многополюсных магнитных систем, выполненных из постоянных магнитов, в различных областях электротехники и устройствах ускорительной техники.

 

ЛИТЕРАТУРА

1.       Постоянные магниты: Справочник / Альтман А.Б., Герберт А.Н., Гладышев П.А. и др.; Под ред. Ю.М. Пятина. – М.: Энергия, 1980. – 488с.

2.       Ледовский А.Н. Электрические машины с высококоэрцитивными постоянными магнитами. – М.: Энергатомиздат. – 1985. – 168с.

3.       Коген-Далин В.В., Комаров Е.В. Расчёт и испытание систем с постоянными магнитами. – М.: Энергия, 1977.