Physics / 6.radiophysics
Bubis E.L.
IAP RAS Nizhny
Novgorod, Russia
Study of the phase contrast technique with photothermal filters
The phase contrast
method proposed by F.Zernike in 1934 is widely used for visualization of optical small-scale
inhomogeneities of a medium (both inherent and induced) in various fields of
physics and engineering from optical microscopy, measurement of weak absorption
of light by a medium, to plasma physics [1-5].
The phase contrast technique
based on nonlinear Zernike cells (filters) started to develop recently [6-15]. As distinct from the schemes employing linear
filters (in the simplest case, Zernike plates responsible for a selective phase
shift of quarter a wavelength between zero and higher space frequencies
participating in the object imaging formation), nonlinear Zernike filters are
optical schemes requiring less adjustment (all-optical, self-adaptive phase
contrast imaging technique), with the necessary
phase shift provided by choosing an appropriate intensity of light entering the
nonlinear medium. The use of nonlinear Zernike cells for analyzing a light wave
phase in adaptive optical systems was proposed in [2]. The present paper deals
with results of the experimental study of a phase-contrast scheme with a
photothermal cell, in which phase mismatch is due to a thermal nonlinearity
mechanism in an absorbing medium. Numerical calculations concerning some
problems of image quality in such systems, taking into account nonlocal
response of a nonlinear medium are given in [12]. Thermal processes in pure
liquids in the field of long laser pulses have been previously considered by
the author (see, e.g., [15]).
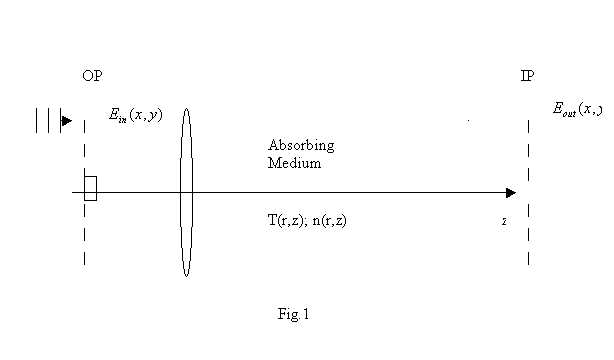
A one-lens scheme of image
formation shown in fig. 1 and analogous to the scheme with a photothermal cell
located in the Fourier plane of the system [6-8] was employed in the
experiment.
Phase object

The objects were illuminated by a Gaussian beam of a
single-mode linearly polarized He – Ne laser of the power P≤ 6mW and the
wavelength λ = 0,63μm. The radiation passed through an object was
focused by a lens (F=6 cm, D=3.5 cm) to the middle of a cell filled with ethyl alcohol
or acetone and an absorber. The value ![]() ≈ 0.2 – 0.6 was
chosen experimentally. Here
≈ 0.2 – 0.6 was
chosen experimentally. Here ![]() is the absorption
coefficient of the medium and
is the absorption
coefficient of the medium and ![]() is its length. A cell with an absorbing medium
is its length. A cell with an absorbing medium ![]() =1-100 mm was used. Images of examined transparent objects
visualized on a screen located at a distance of 10 m from the lens were
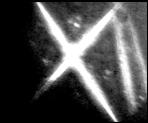
photographed with a digital camera. Figures 2 show visualized images of a cross
of two light guides (100
=1-100 mm was used. Images of examined transparent objects
visualized on a screen located at a distance of 10 m from the lens were
photographed with a digital camera. Figures 2 show visualized images of a cross
of two light guides (100![]() ) placed in a quartz cell filled with vaseline oil at the
radiation a)
) placed in a quartz cell filled with vaseline oil at the
radiation a) ![]() and b)
and b) ![]() ; in the case b) one distinctly observes the effect of image
inversion with some distortions caused by beam self-action in the medium, ñ)linear
dark-field method.
; in the case b) one distinctly observes the effect of image
inversion with some distortions caused by beam self-action in the medium, ñ)linear
dark-field method.


All the
results are obtained at a power that does not lead to a marked self-action of
the beam in the absence of a phase object. At the incident power Ð≥ 5 mW a typical aberration picture of thermal
defocusing was seen in the far zone.
Therefore, basic properties of a phase
contrast scheme with photothermal Zernike cell are studied. The required level
of scheme operation corresponds to the initial stage of developing thermal
self-action of an illuminating laser beam, which is an important and most
low-threshold nonlinear-optical phenomenon for continuous and quasi-continuous
laser radiation.
References
[1] Francon
M. Le Microscope a Contraste de Phase et Le Microscope Interferentiel. Paris: Editiondu center national de la recherence
scientifique. 1954.
[2]Vorontsov M.A., Koryabin M.A., Shmalhauzen
V.I. Controlled optical
systems. M.: Nauka. 1988.
[3] H. Weisen.//
Rev.Sci.Instrum.,1988, 59(8), pp. 1544 – 1549.
[4] Roland C.Anderson and Steven Lewis
//Appl.Opt,1985,Vol.24,No.22, 3687.
[5] Babin A.A., Bubis E.L., Lozhkarev V.V.et al // Quantum Electronics. 1998. V. 28, ¹8. Ð. 738–740.
[6] Tchernega N.V., et al. // Quantum Electronics ,
1989, ¹12, ñ. 2530 -2538.
[7] Iturbe-Castillo M.D.et al.// Opt.Eng. 2001, Vol 40. N 11. P. 2367 – 2368.
; Treviño-Palacios C.G. et al // Appl.Opt., 2003, Vol.42, No.25, pp.5091
– 5095.
[8] Bubis E.L. // Preprint of the
Institute of Applied physics of RAS. N. Novgorod. 2006. ¹ 698.
[9] Yelleswarapu C.S.et al //Applied
Physics Letters. 2006. V. 89. P. 211116-1.
[10]
Bubis E.L., Matveev A.Z. // Tech.Phys.Lett. 2007, Vol.33, No.6, p.454.
[11]
Bubis E.L.,et al // Proc. SPIE, Vol.
6729, 2007. p.52.
[12]
Bubis E.L., Matveev A.Z. // Proc.SPIE, 2007, Vol. 6729, p.82.
[13]
Bubis E.L // Tech.Phys.Lett. 2008, Vol.34, No.6,pp.510 – 511.
[14]
Bubis E.L // Instruments and Experimental Techniques, 2009, Vol. 52, No. 1, pp.
108–109
[15]
Bubis E.L.,et al // Optics and Spectroscopy, 1988, Òîì 65, ¹6, ñ. 1281 -1286.