Физика/1. Теоретическая
физика
Магеррамов М. А.
Азербайджанский
Государственный Экономический Университет
Уравнения и модели,
описывающие теплопроводность плодоовощных соков
В
данной работе нами исследована теплопроводность ряда фруктовых соков.
Исследованный диапазон параметров состояния составил: для температуры (Т)-
278.1 – 393.1 К, для массовой доли сухих веществ (С)- от натурального до 60%;
Исследования
при температуре выше точки кипения при нормальном давлении проводились при
повышенном давлении в системе 2 МПа.
Анализ
полученных экспериментальных данных показал, что темпе-ратурная зависимость
λ в исследованном интервале не является линейной, и описать эту
зависимость можно полиномом второй степени. Концентра-ционная зависимость
близка к линейной, однако в точности не является таковой.
Для
температурной зависимости теплопроводности на примере гра-натового сока
получены следующие выражения:
С=16%, ![]() (1)
(1)
С=46%, ![]() (2)
(2)
Для
точного описания опытных данных нами разработана матема-тическая модель,
основанная на квадратичном представлении зависимос-тей теплопроводности от
температуры и концентрации:
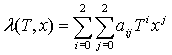 , (3)
, (3)
где: λ
– коэффициент теплопроводности, Вт/(К∙м); Т – температура, °С;
x – концентрация сухих веществ,%; aij – эмпирические коэффициенты;
или в раскрытом виде:
![]() , (4)
, (4)
где концентрационная
зависимость параметров a0(x), a1(x) и a2(x) может
быть представлена в виде:
![]() ;
; ![]() ;
; ![]() (5)
(5)
Как видим, уравнение содержит 9 регулируемых параметров.
Уменьшение коэффициентов существенно облегчает процедуру расчетов, в особенности
это необходимо в практических приложениях. С этой целью был проведен
дополнительный анализ с выяснением границ потерь точности при описании
уравнением опытных данных в случае применения линейной функ-ции для
теплопроводности. С достаточной для практики точностью модель может быть
представлена в виде:
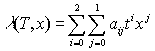 , (6)
, (6)
где: λ – коэффициент теплопроводности,
Вт/(К∙м), Т – температура, °К,
x – концентрация сухих веществ,%, aij – эмпирические коэффициенты.
Поскольку
зависимость коэффициента теплопроводности была опи-сана прямолинейной функцией,
можно без существенной погрешности экс-траполировать λ=f(с) на
нулевую концентрацию. Сравнение температурной зависимости полученных при такой
процедуре величин λ0 с данными по чистой воде может
представлять определенный интерес.
Анализ
данных показывает что, величины λ0 меньше теплопровод-ности
воды в среднем на 2- 4%. Температурная зависимость λ0
практически аналогична линии λ=f(Т) для воды. Это косвенно может служить подт-верждением надежности
опытных данных.
По
результатам измерений теплопроводности мандарина предложено следующее уравнение
в виде:
λ=0.496-3.1×10-3c+3.835×10-3T-3.61×
×10-5cT-1.758×10-5T2+2.459×10-7cT2 (7)
Уравнение описывает опытные данные с
погрешностью не более ±1.5- 2%.
В
литературе известна модель, предложенная Лосинским (Losenicky (1969)), в основе которой лежит
представление коэффициента теплопро-водности раствора или смеси посредством
величины теплопроводности чистого растворителя. Т.е., уравнение описывает, по
сути, отклонение теплопроводности смеси (раствора) от чистого растворителя. В
нашем слу-чае, основным компонентом соков как очевидно, является вода. Исходя
из этого, мы использовали данные о чистой воде в качестве слагаемого, от-ветственного
за растворитель.
Модель
разрабатывалась для сливового, малинового, вишневого и персикового соков.
Аналитический вид модели для малинового и вишневого соков представлен ниже:
малиновый сок: ![]() (8)
(8)
вишневый сок: ![]() (9)
(9)
Среди
немногочисленных данных о теплопроводности фруктовых соков встречающихся в
литературе, нами обнаружены в частности сведения о виноградном соке.
Анализ
полученных данных для виноградного сока показывает, что температурная
зависимость коэффициента теплопроводности приближается к линейной при
увеличении содержания сухих веществ. Концентрационная зависимость λ близка
к линейной, что позволяет экстраполировать ее в область высокого содержания
сухого вещества.
Уравнение
для коэффициента теплопроводности виноградного сока имеет вид: λ=0.567-3.447×10-3 +
9.094×10-4t-3.864×10-6ct (10)
Уравнение
описывает опытные данные со среднеквадратичной погрешностью не более 2%.
Для
яблочного сока нами предлагается следующее уравнение для описания
теплопроводности:
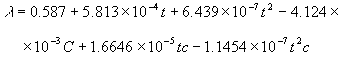 , (11)
, (11)
которое описывает
опытные данные с погрешностью не более 2%.
Гинзбург
А. С. и др. (1980) предложили уравнение, устанавливающее функциональную связь
между теплопроводностью, плотностью и теплоемкостью: ![]() ,
(12); где
,
(12); где ![]()
Здесь:
АТ – инвариант, cT – удельная теплоемкость, αT – коэффициент,
характеризующий степень ассоциации, M
– молекулярная масса.
В
основе этого уравнения лежит формула, предложенная Предводи-телевым. Уравнение
позволяет рассчитать коэффициент теплопроводности, если известна теплоемкость и
плотность. Вместе с тем в формулу входят параметры, определение которых связано
с определенными трудностями и вносит дополнительную погрешность.
В
данной работе мы поставили цель определить аналитические зависимости, которые
позволили бы проводить экстраполяцию экспери-ментальных данных на более высокие
параметры состояния, а также уста-новить простую связь между теплопроводностью
и плотностью. В отличие от уравнения (12), это уравнение не требовало бы
наличия величины теплоемкости. Если данные о плотности различных фруктовых
соков в литературе встречаются, то сведения о теплоемкости, как правило, крайне
редки.
Представляет
интерес выявить зависимость теплопроводности от плотности при фиксированной
температуре, т.е. при различных концентра-циях сухого вещества, и при
фиксированной концентрации, когда на полу-ченной зависимости отражалось бы влияние
температуры.
На
основании полученных опытных величин нами предложено уравнение, устанавливающее
связь двух исследуемых свойств между собой и от температуры в аналитическом виде:
![]() (13)
(13)
где: λ-теплопроводность, Вт/(м∙К),
ρ – плотность, г/см3,
T -температура, К,
A – параметр.
Уравнение
(13), имеющее простой вид, с высокой точностью передает опытные значения
теплопроводности. Как будет меняться параметр А в зависимости от типа сока – предмет дальнейших исследований.
Преимущества
этого уравнения связаны с отсутствием необходимости располагать данными о
теплоемкости, а также в том, что оно в явном виде содержит зависимость от
температуры.
Нам
представляется важным разработка моделей описывающих теплопроводность как
функцию других теплофизических свойств, в част-ности температуропроводности,
вязкости и др. При наличии информации о последних, имелась бы возможность
прогнозирования данных о тепло-проводности различных соков.
Нами
предпринята попытка создания модели, связывающей тепло-проводность и
температуропроводность. Графоаналитический анализ опытных данных о
теплопроводности и температуропроводности апельси-нового сока показал, что
имеется практически близкая к линейной связь этих свойств.
Уравнения,
устанавливающие связь теплопроводности и темпера-туропроводности для
апельсинового сока имеют вид:
С=14%, ![]() , R2=0.991; С=40%,
, R2=0.991; С=40%, ![]() , R2=0.996 (14)
, R2=0.996 (14)
Уравнения
корреляции теплопроводности с температуропроводностью для гранатового сока
С=20%, ![]() , R2=0.996;
С=50%,
, R2=0.996;
С=50%, ![]() , R2=0.996(15)
, R2=0.996(15)
Не
меньший интерес представляет установление корреляции между вязкостью и теплопроводностью.
В литературе имеется немало сведений о вязкости, и наличие модели, связывающей
эти два свойства, могло бы пос-лужить существенным облегчением при разработке и
проектировании новых промышленных установок по переработке плодово-ягодных
культур.
Модель
разрабатывалась на основе экспериментальных данных о теплопроводности и
вязкости сливового сока.
Уравнение,
описывающее корреляцию вязкости и теплопроводности:
![]() (16)
(16)
Для
сливового сока определены следующие коэффициенты:
С=13%, λ=6.466×10-1-1.157×10-1η+3.28×10-2η2,
R2=0.999
(17)
С=38%, λ=5.252×10-1-3.10×10-2η+3.0×10-3η2,
R2=0.986 (18)
На
основе графоаналитических анализов предпринята попытка разработки модели для
корреляции теплопроводности и текучести.
В
результате получено уравнение, устанавливающее связь между теплопроводностью и
текучестью для абрикосового сока:
![]() (19)
(19)
Для
сока с 25% содержанием:
λ=4.619×10-1+9.64×10-2f-2.31×10-2f2, R2=0.992 (20)
Для сока с 40%
содержанием:
λ=4.225×10-1+2.079×10-1f-6.59×10-2f2, R2=0.990 (21)
Обобщенное
уравнение, не зависящее от концентрации для абрикосо-вого сока может быть
записано в виде:
![]() , (22)
, (22)
Теплопроводность
плодоовощных соков ведет себя в зависимости от температуры подобно воде,
вследствие чего выбор математического выраже-ния для температурного ряда не представляло
сложности. Мы ограничились квадратичным представлением функции λ=f(Т). Всесторонний анализ полу-ченных
данных позволяет рекомендовать в качестве универсальной модели для описания
коэффициента теплопроводности выражение вида (3). Данная модель с высокой
точностью передает изменения теплопроводности с температурой и концентрацией, и
погрешность не превышает экспериментальную. Модель применима для широкого
интервала концентраций и температур.
В
случае если концентрационный интервал не столь широк, в частности до 30-40%,
возможно использование модели (6) со всего лишь 6 эмпирическими коэффициентами.
В литературе часто
делались попытки связать теплопроводность и плотность жидкости, и указывалось
на их тесную связь. Модель (13), разработанная в рамках данной работы, имеет
простой вид и позволяет проводить расчет теплопроводности при изменении
температуры. Явное преимущество данной модели в наличии явной температурной
зависимости, что однозначно соотносит рассчитанную величину теплопроводности к
конкретной температуре.
Разработанные
модели, устанавливающие корреляции теплопровод-ности с температуропроводностью
(14,15), с вязкостью (16), с текучестью (19) позволяют проводить расчет
теплопроводности при известных вели-чинах указанных свойств. Как показал анализ,
теплопроводность и темпе-ратуропроводность имеют линейную корреляцию.
Использование же линейной функции для выражения связи теплопроводности с
вязкостью или текучестью приводит к существенным погрешностям. Вследствие этого
использовали полином второй степени (16) и (19). Каждая модель с достаточной
точностью связывает отмеченные свойства.