Асистент Шуллє Ю.А.

Вінницький національний технічний університет, Україна

Прогнозування навантажень електротехнічних комплексів з використанням фрактального аналізу часових рядів

У останні десятиліття дослідники в багатьох областях науки направляли свої зусилля на виявлення загальних рис в нелінійних процесах, що протікають в досліджуваних системах. Це привело до побудови нового міждисциплінарного підходу, що дістав назву "синергетика" [1]. Ключовою концепцією синергетики є концепція "параметрів порядку", тобто декількох основних ключових змінних, які визначають, "підпорядковують" усі інші ступені свободи системи. Математичне моделювання багатьох систем показало, що їх поведінка дійсно визначається кінцевим числом параметрів порядку, іншими словами, з практично нескінченної, важко осяжної безлічі значень спостережуваних функцій і станів можна здійснити перехід до кінцевого, а іноді невеликого числа змінних (параметрів). Синергетика на перше місце ставить концепцію хаосу, тобто той факт, що хаос лежить в природі будь-якої еволюційної системи. В цьому випадку факт присутності хаосу може призводити до помилок у разі використання традиційного інструментарію математичної статистики. Теорія хаосу не лише пояснює біфуркаційні явища (великі спади або великі викиди), але і прямо говорить, що їх неможливо передбачити. З цієї причини багато технічних аналітиків обґрунтовано припустили, що розпізнати в хаотичному русі нові закономірності їм допоможе фрактальна геометрія. Фрактали у реальному світі обумовлені глобальними статистичними структурами, що одночасно породжують локальні випадковості, тобто хаос і порядок співіснують. Не існує абсолютно точного визначення фракталу. Одне з визначень представляє фрактал як деяку самоподібність, тобто фрактал - це структура, що складається з частин, які в якомусь сенсі подібні до цілого.

Розглянемо необхідність використання нової - фрактальної статистики в математичному моделюванні електроенергетичних процесів і систем. Відмітимо, що класична статистика базується на центральній граничній теоремі, яка стверджує, що у міру проведення все більшого числа спостережень, граничний розподіл випадкових значень буде нормальним розподілом. Це означає, що події мають бути незалежними, тобто не повинні впливати одна на одну і при цьому усі вони повинні мати однакову ймовірність настання. Передбачається, що поведінка більшості реальних електроенергетичних систем підкоряється нормальному або "майже нормальному" закону. Однак іноді це не так, тому з'явилося усвідомлення того, що для адекватного моделювання потрібний інструментарій нової статистики, відмінний від стандартної.

Відповідний інструментарій нової статистики існує у вигляді непараметричної методології, яка була відкрита Х.Е. Херстом - британським гідрологом. Херст дав нову статистичну методологію для розрізнення випадкових і невипадкових систем, постійності трендів і тривалості циклів, тобто метод нормованого розмаху, або - аналіз, що використовується для розрізнення випадкового часового ряду і фрактального часового ряду.

Метою даної роботи є розробка підходу для прогнозування електричного навантаження в реальному масштабі часу з врахуванням його фрактального характеру, що базується на нейромережевих технологіях.

Проблемі моделювання самоподібного (фрактального) потоку даних присвячена значна кількість наукових праць [3,4]. Результати цих досліджень у класичному варіанті дозволяють визначити значну кількість характеристик навантажень електротехнічних комплексів. У більшості запропонованих алгоритмів присутній суттєвий недолік – необхідний значний час для отримання і обробки інформації про досліджуваний потік даних. Проте, реальне функціонування електротехнічних комплексів потребує управління в реальному часі. У цьому випадку вирішити протиріччя, що виникло, у змозі теорія нейродинаміки, в основі якої лежать методи штучних нейронних мереж, хаосу та фракталів.

Для вивчення хаотичних процесів, таких як, наприклад споживання електроенергії може бути використаний показник Херста, що дозволяє визначити хаотичність або стохастичність аналізованого процесу. У класичному вигляді цей показник може бути отриманий із співвідношення

, (1)

де R – максимальний розмах досліджуваної величини; S – її середньоквадратичне відхилення; N – час досліджень (або об’єм вибірки), – деяка постійна; H – показник Херста.

Величина коефіцієнта H характеризує відношення сили тренда (детермінований фактор) до рівня шуму (випадковий фактор). Показник Херста може класифікувати часові ряди, відрізняючи випадковий ряд від невипадкового. Якщо показник Херста Н>1/2, випадковий процес називають персистентним: таким, що підтримує поточну тенденцію. Наприклад, якщо значення перемінної зростає, то в наступний момент часу також буде зростання. Процеси із показниками Н<1/2 називаються, відповідно, антиперсистентними: таким, що не підтримує поточну тенденцію. Випадковий процес із Н=1/2 відповідає броунівському випадковому процесу, для якого відсутні ефекти пам’яті або мають місце процеси, в яких тренд відсутній.

Аналізуючи (1) можна сказати, що це форма вираження різних сигналів на фрактальній площині, яка утворена логарифмічними координатними осями, а показник Херста H визначає нахил апроксимуючої прямої фрактальної лінії до осі абсциса. Алгоритм обчислення показника Херста представлений у вигляді:

1. Середнє значення часового ряду ;

2. Відхилення ряду вимірів від середнього ;

3. Розмах часового ряду ;

4. Стандартне відхилення ;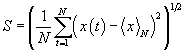

5. Показник Херста .

Визначаючи параметр Херста для функціонування електротехнічного комплексу, можна провести прогнозування необхідних параметрів системи [5,6]. Але класичний метод Херста має ряд недоліків, серед яких неможливість обчислення показника в реальному масштабі часу через значний ріст об’єму обчислень. Для усунення даного недоліку скористаємось покроковим рекурентним алгоритмом

, (2)

де k=1, 2, ... – відповідні часові інтервали агрегування даних спостережень процесу реального функціонування електротехнічного комплексу.

З виразу (2) видно, що показник Херста може уточнюватись на кожному кроці агрегування без попереднього запам’ятовування значень потоку даних. Реалізація наведеного алгоритму визначення H може бути спрощена за допомогою нейромережевих технологій. Результат обчислень параметру Херста в великій мірі залежить від параметру і об’єму вибірки, що може призвести до того, що для одної і тієї ж реалізації потоку даних можуть бути отримані різні, а іноді і протилежні результати. Цю проблему можна вирішити за рахунок використання нейромережевих технологій, які пов’язані з алгоритмами навчання та аналізу реальних систем. Тоді переписавши (2) у вигляді, введемо навчаючий сигнал для лінійної прямонаправленої нейромережі типу адаліни, для якої використаємо алгоритм навчання для отримання оцінок невідомих параметрів у вигляді

;

. (3)

В цьому випадку для розрахунку показника Херста та параметра мережі може бути застосована відповідна архітектура штучної нейронної мережі, яка буде функціонувати паралельно до контрольованого процесу, та виявляти зміни, що виникають в реальному часі.

В другому варіанті реалізації нейромережевого підходу до прогнозування параметрів споживання електроенергії в якості основного елементу використаємо нейромережу з радіальними базисними функціями збудження (рисунок 1).

251658240

Рисунок 1 - Архітектура p-r-k мережі з радіально-базисними функціями

Вихідний сигнал такої мережі має вигляд , де - вихід нейромережі (прогнозовані параметри); k – розмірність вихідного вектору; – вектор, що складається з r радіальних базисних функцій нейронів прихованого шару, з елементами , де – вхідний сигнал нейромережі (параметри поточного потоку даних); M – розмірність вхідного вектора; – координати центрів активаційних функцій, , r – кількість схованих нейронів в мережі; – ширина активаційних функцій; W – вихідна вагова матриця мережі (розмірність ).

Для такої мережі може бути застосований наступний алгоритм навчання:

1. Оберемо розмір прихованого шару R, що рівний кількості тренувальних шаблонів. Синаптичні ваги нейронів схованого шару приймемо рівними 1.

2. Розмістимо центри активаційних функцій нейронів схованого шару в точках x простору вхідних сигналів мережі, які входять в набір тренувальних шаблонів

3. Оберемо ширину вікон активаційних функцій нейронів прихованого шару , достатньо великими, але так, щоб вони не накладались один на одного в просторі вихідних сигналів.

4. Визначимо ваги нейронів вихідного шару мережі , для чого надамо мережі весь набір тренувальних шаблонів і в результаті отримаємо набір лінійних рівнянь, який можна записати в матричному вигляді, де D – матриця (розміром ) бажаних виходів (вихідних шаблонів); Ф – інтерполяційна матриця (розміром) елементи якої де .

Вирішення системи рівнянь у вигляді забезпечує проходження інтерполяційної поверхні через всі точки тренувального набору шаблонів.

Висновок

В даній роботі було показано можливість прогнозування навантажень електротехнічних комплексів з використанням фрактального аналізу часових рядів. Для математичного моделювання і прогнозування процесів споживання електроенергії необхідно використовувати запропоновану методику оцінювання параметра Херста, яку можна застосовувати для дослідження фрактальної структури часових рядів різної природи. Запропонований метод прогнозування електричного навантаження в реальному масштабі часу, на основі теорії штучних нейронних мереж.

Література

1. Занг В.Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории. Пер. с англ. - М.: Мир, 1999. - 336 с.

2. Федер Е. Фракталы. Пер. с англ. - М.: Мир, 1991.- 254 с.

3. Петерс Э. Фрактальный анализ финансовых рынков: применение теории хаоса в инвестициях и экономике. - М.: Интернет-трейдинг, 2004. - 304 с.

4. Шиян А.А., Шуллє. Ю.А. Метод оцінювання та ідентифікації характеристик і високоамплітудних відхилень електричних навантажень електротехнічних комплексів. /Вісник Хмельницького національного університету. Технічні науки, 2010. - №1. - С. 215 - 217.

5. Шиян А.А., Шуллє Ю.А. Сценарії оптимізації та прогнозування управління електричними навантаженнями електротехнічних комплексів. / Вісник Хмельницького національного університету. Технічні науки, 2010. - №2. - С. 122-124.