Медицина/Терапия.

А.С. Орлов

НПО Автоматики имени академика Н.А.Семихатова, г. Екатеринбург.

О ВЛИЯНИИ НЕЛИНЕЙНОСТИ ПАРАМЕТРОВ БОЛЬШОГО КРУГА КРОВООБРАЩЕНИЯ НА ФОРМУ ПУЛЬСОВОЙ ВОЛНЫ.

Согласно расчетов [2] средняя податливость стенок сосудов С=dV/dP артериального русла большого круга кровообращения здорового человеческого организма составляет 1,69 мл/мм рт.ст.

Считается, что основной вклад в податливость стенок сосудов вносит аорта и другие артерии эластического типа, которые обуславливают амортизирующий эффект [6, стр.506], заключающийся в сглаживании периодических систолических волн кровотока. Эти сосуды называют еще «компрессионной камерой» или согласно модели Frank являются основным отделом сосудистой системы, работающими как «воздушный колпак» [5, стр 80].

Свой вклад в общую податливость стенок сосудов вносят и сосуды мышечного типа, такие как плечевая артерия (ПА) бедренная артерия (БА), мелкие артерии, артериолы и прекапилляры. Оценим вклад каждой составляющей в общую величину податливости стенки артериального русла большого круга кровообращения. Будем учитывать вклад следующих основных составляющих артериального русла.

§ Общей сонной артерии (ОСА),

§ Аорты,

§ Плечевой артерии (ПА), объединенной с лучевой и локтевой артериями;

§ Бедренной артерии (БА), объединенной с передней и задней большеберцовой артериями и малоберцовой артерией;

§ Другие артерии в том числе мелкие артерии, артериолы и прекапилляры.

Общая сонная артерия и аорта являются сосудами эластического типа, остальные артерии – сосудами мышечного типа.

С учетом диаметров ОСА и ПА, приведенных в [2] будем использовать значения геометрических размеров артерий, приведенных в таблице 1.

Скорость распространения пульсовой волны (СПВ) в кровеносном сосуде с прикрепленными стенками описываетcя выражением Моэнса-Кортевега [4]

U =√ h•E/(d•ρ) (1)

где

h – толщина стенки сосуда,

d – диаметр сосуда,

E – эффективный модуль Юнга стенки сосуда

ρ – плотность крови, равная 1,06 10³ кг/м³.

Таблица 1

Наименование артерии	Внутренний диаметр артерии [мм]	Сечение артерии [см^2]	Обобщенная длина артерии [см]	Объём артерии [см^3]
Общая сонная артерия	7	0,38	17	6.5
Аорта	24	4,52	38	172
Плечевая артерия	4	0,13	50	6,3
Бедренная артерия	5	0,2	90	17,7

Выражение 1 можно преобразовать к выражению для скорости распространения волны через параметры: объем сосуда (V) и податливость стенки C=dV/dP [6, стр 504]

U=√V/(C•ρ) (2)

Величина V/C носит название объёмного модуля упругости, обратная величина носит название – коэффициент растяжимости Dp, который определяется через параметры сосуда и приращение давления [1]

Dp= 2•ΔD/(ΔP•D) = C/V (3)

где:

D – диаметр артерии при диастолическом давлении,

ΔP – приращение артериального давления,

ΔD – приращение диаметра артерии, при изменении давления в ней на ΔP.

Скорость распространения пульсовой волны и коэффициент растяжимости связаны соотношением

U=√1/(Dp•ρ) (4)

Коэффициент растяжимости для ОСА по данным [1] составляет 33•10^-6 1/Па.

Подставляя в (4) значения ρ и Dp для ОСА и получим

Uоса=√1/(33•10^-6•1,06) = 5,34 м/с

Из выражения (3) можно оценить относительное изменение диаметра артерии по приведенному значению Dp. При ΔP = 40 мм рт.ст.=5320 Па, получим

ΔD/D = Dp ΔP/2 = 33•10^-6 5320/2=0,088

Т.е. относительное изменение диаметра сонной артерии за время сердечного цикла составляет 8,8%.

Из выражения (2) определим величину податливости стенки артерии

С = V/(U²•ρ) (5)

При подстановке в выражение 5 величин в системе СИ, получим значение С в [м³/Па]. Для перевода в единицы измерения [мл/мм рт.ст.], необходимо умножить эту величину на 133•10⁶.

Для молодого организма соотношение СПВ мышечного типа к СПВ эластического типа составляет 1,2-1,3 [5, стр. 66], поэтому без большой погрешности СПВ для сосудов мышечного типа, в нашем случае, можно принять равной 6,7 м/с.

В таблице 2 приведены средние значения для податливости стенок артерий ОСА, ПА, БА, вычисленных по выражению 5 для молодого организма с учетом объема артерий таблица 1..

Таблица 2

Наименование артерии	Скорость распространения пульсовой волны, [м/с]	Податливость стенки артерии (С), [мл/мм рт.ст.]
ОСА	5,34	0,029
ПА	6,7	0,018
БА	6,7	0,049

Просуммировав значение податливости стенок артерий ПА, БА, ОСА и умножив их на два, т.к. каждой артерии в организме по две, получим, что суммарная податливость стенок основных артерий составит 0,19 мл/мм рт.ст., что составляет 11% от общей податливости артериального русла.

В таблице 3 приведены характеристики аорты, вычисленные на основании зависимости давления от объема аорты для различных возрастных групп [6, стр 512]

Суммарная податливость стенок основных артерий (табл. 2) и аорты (таблица 3), для молодого организма, составит 0,86 мл/мм рт.ст. Вычитая эту величину из среднего значения податливости стенок артериального русла, получим среднюю податливость стенок артериального русла без учета податливости стенок аорты, ПА, БА, и ОСА, которая составит 1,69 – 0,86=0,83 мл/мм рт.ст., что даже больше, чем вклад аорты. Таким образом, роль компрессионной камеры в организме играет не только аорта, но и мелкие артерии и артериолы. Этот эффект хорошо заметен при наблюдении модуляции светового потока через ногтевую фалангу пальца, используемый в пульсовых оксиметрах.

Таблица 3

Возраст [годы]	16 - 39	40 – 59	60 - 83
Максимальное значение податливости стенки аорты Смак при Р=80 мм рт.ст. [мл/мм рт.ст.]	0,78	0,58	0,24
Минимальное значение податливости стенки аорты Смин при Р=120 мм рт.ст. [мл/мм рт.ст]	0,56	0,42	0,20
Среднее значение податливости стенки аорты Сср= (Смак+ Смин)/2 [мл/мм рт.ст]	0,67	0,5	0,22
Средний объём аорты [мл]	170	210	250
Скорость распространения пульсовой волны [м/с]	5,64	7,26	11,94
Смакс/Смин	1,39	1,38	1,2
ΔС=(Смакс-Смин) [мл/мм рт.ст]	0,22	0,16	0,04
Кс=ΔС/Смакс	0,28	0,28	0,17

С возрастом из-за снижения податливости стенок сосудов увеличивается СПВ. Так в сосудах мышечного типа СПВ увеличивается примерно в 1,5 раза [5, стр.66], а в аорте СПВ увеличивается, примерно, в 2 раза. Поэтому соотношения СПВ в сосудах мышечного типа к СПВ эластического типа от 1,2 - 1,3 у молодого организма снижается к 1,0 у пожилого организма.

Податливость стенок сосудов за время систолы изменяется от Смакс до Смин. При аппроксимации этого изменения линейной зависимостью, податливость стенки сосудов от давления будет описываться следующим выражением:

С(Р) = Смакс – (ΔС/ΔР)•(Р – Рмин)

где:

ΔС = Смакс – Смин.

Р – текущее значение АД,

ΔР – пульсовое давление, равное (Рмакс – Рмин),

Рмакс – систолическое АД,

Рмин – диастолическое АД,

Соотношение между максимальным, средним и минимальным значения податливости стенки сосуда определяются следующим выражениями:

Сср = (Смакс+Смин)/2

Смакс= Сср/(1 – Кс/2)

Кс = ΔС/Смакс = (1 – Смин/Смакс)

(ΔС/2)/Сср= Кс/(2 – Кс)

За время сердечного цикла с ростом давления происходит увеличение радиуса кровеносных сосудов, что приводит к уменьшению гидродинамического сопротивления (ГДС).

Аналогично изменению податливости стенок сосудов за время систолы, можно так же аппроксимировать изменение ГДС прямой линией. В этом случае зависимость R(Р) будет выглядеть

R(Р) = Rмакс – (ΔR/ΔР)•(Р – Рмин)

Соотношения между максимальным, средним и минимальным значением ГДС будут определяться следующими выражениями:

Rср = (Rмакс+Rмин)/2

Rмакс = Rср/(1–Кr/2)

Кr = ΔR/Rмакс =(1 – Rмин/Rмакс)

(ΔR/2)/Rср= Кr/(2 – Кr)

Можно показать, что изменение объёма сосудов при изменении давления от Рмакс до Рмин, при линейной аппроксимации С(Р), определяется выражением

ΔV=Сср•ΔР (6)

Подставив в выражение 6 значения Сср=1,69 мл/мм рт.ст., ΔР = 40 мм рт. ст., получим изменение объёма артериального русла при изменении давления от Рмакс до Рмин равное 67,6 мл.рт.ст. Эта величина меньше ударного объема сердца (95 мл), за счет того, что часть ударного объема успевает пройти через капилляры за время систолы.

Оценим относительное изменение ГДС за время сердечного цикла. Изменение объема артерии к изменению его внутреннего радиуса или диаметра можно описать выражением

dV/V = 2•dr/r = 2•dD/D (7)

где:

V – первоначальный объём артерии, например, при АД, равном Рдиаст,

r – первоначальный радиус артерии, например, при АД, равном Рдиаст

dV – изменение объема артерии при изменении давления в ней на dР,

dr - изменение радиуса артерии при изменении давления в ней на dР,

D - первоначальный диаметр артерии, например, при АД, равном Рдиаст,

dD - изменение диаметра артерии при изменении давления в ней на dР,

На основании закона Пуазейля для ГДС можно записать

dR/R = - 4dr/r = -2•dV/V (8)

R – первоначальное изменение ГДС, например, при АД, равном Рдиаст,

dR – приращение изменения ГДС при изменении давления в нем на dР

Разделив левую и правую часть (7) на dР, преобразуя и учитывая, что С=dV/dP, получим

V/С= dР/(2•dr/r) (9)

Из выражения (2) следует

V/С = U²•ρ (10)

Приравнивая (9) и (10), преобразуя и переходя к конечным приращениям, получим

Δr/r = ΔР/(2•U²•ρ)

Определим относительное изменение радиуса артерии мышечного типа при ΔР = 40 мм рт.ст.(5320 Па), U = 6,7 м/с, ρ = 1,06 кг/м³ , получим

Δr/r = 40•133/(2•6,4²•1,06•10³) = 0,056

Т.е. изменение радиуса артерии мышечного типа происходит на 5,6 %, при этом изменение ГДС составит

ΔR/R = - 4•dr/r = -4•0,056 = -0,22

т.е. ГДС уменьшается за счет расширения сосудов на 22%.

Для пожилого организма СПВ будет выше, например, 11 м/с, а ΔР = 55 мм рт.ст., тогда относительное изменение радиуса сосудов составит

Δr/r = 55•133/(2•11²•1,06•10³) = 0,028,

а изменение ГДС составит

ΔR/R = - 4dr/r = -4 0, 028 = -0,11

Из расчетов видно, что с увеличением возраста изменение ГДС за время сердечного цикла будет примерно в 2 раза меньше.

Исходя из (7) можно оценить среднее значение объема артериального русла. Так при АД, равном Рмин, объём артерий будет минимальным – Vмин, а ГДС максимальным – Rмакс, поэтому выражение (7) для конечных приращений можно записать в следующем виде

ΔR/Rмакс = -2ΔV/Vмин (11)

где:

ΔR – изменение ГДС за время сердечного цикла,

Rмакс – максимальное значение ГДС при АД, равном Рмин

ΔV – приращение объема артерии за время сердечного цикла

Vмин – минимальный объем артерии при АД, равном Рмин.

Из выражения (11) с учетом (6) следует

Vмин = -2Сср•(Рмакс-Рмин)/(ΔR/Rмакс) (12)

Можно показать, что

Vср = Vмин √(Rср/Rмин) = Vмин √ [(1-Kr/2)/(1- Kr)] (13)

Для молодого организма Kr = -0,22. Сср = 1,69 мл/мм рт.ст., (Рмакс-Рмин) = 40 мм рт.ст.. Подставив эти значения в (12), а затем в (13), получим, что Vср = 655 мл. Вычисленное значение незначительно отличается от данных для среднего суммарного объема сосудов системного кровообращения (аорта, крупные и мелкие артерии) для среднего организма, которое равно 700 мл [6, стр.509].

Определение характера зависимости P(t) на участке систолы при учете зависимости податливости стенки сосудов и ГДС от АД проще получить, решая задачу численным методом. Для этого необходимо разбить интервал t₁ на N равных интервалов Δ_t, считая при этом, значение скорости кровотока (Un), значение податливости стенки сосудов (Cn) и значение ГДС (Rn) на этом интервале постоянными.

Можно показать, что выражение для зависимости P(n) при линейной апроксимации изменения величин податливости и ГДС на участке систолы, будет иметь следующий вид:

P(n) = Ро•exp (- Δ_t•n/τср₀) + (Vо•Rср/t₁) (1-exp (-Δ_t•n/τср₀)•γ_n (14)

1 ≤ n ≤ N

где:

Ро –давление на начальном участке систолы,

τср₀ – средняя постоянная времени

Vо – ударный объем сердца,

Rср – среднее значение ГДС,

t₁ – длительность систолы,

γ_n – коэффициент, учитывающий отличие параметров Un, Rn, Cn от их средних значений.

Средняя постоянная времени определяется по следующему выражению

n

τср₀ = n/(Σ (1/τ_i)) (15)

i=1

1 ≤ i ≤ n

коэффициент γn определяется по следующему выражению

n

γ_n=Σ(Ui/Ucp•Ri/Rcp•Si/Scp)(1–exp(–Δ_t/τ_i))•exp(–Δ_t (1–n)/τср_i)/

i=1

/(1–ехр(–Δ_t•n/τср₀)) (16)

где:

Ui, Ri, Si –значения cкорости кровотока, гидродинамического сопротивления, сечение артериального русла соответственно на i-м интервале,

Uср – средние значения скорости кровотока, гидродинамического сопротивления, сечения артериального русла соответственно на участке систолы,

τ_i – постоянна времени на i-м интервале, τ_i = Ri Ci,

τср_i – среднее значение постоянной времени на i-м интервале.

n

τср_i = (n-1) / (Σ (1/τ_j)) (17)

j=(i+1)

1 ≤ i ≤ n

Определение характера зависимости P(t) на участке диастолы при учете зависимости податливости стенки сосудов и ГДС от АД можно так же получить, решая задачу численным методом. Для этого необходимо разбить интервал t₂ – время диастолы на М равных интервалов Δ_t, считая при этом значение податливости стенки сосудов и значение ГДС на этом интервале постоянными.

Можно показать, что в этом случае выражение для зависимости P(t) будет иметь следующий вид:

P(m) = Р_N•exp (–Δ_t•m/τ_срm) (18)

1 ≤ m ≤ M

где:

τ_срm – средняя постоянная времени для m-го интервала.

m

τ_срm = m/(Σ (1/τ_i)) (19)

i=1

1 ≤ i ≤ m

τ_i = Ri Ci

Р_N – значение давления в конце систолы.

На рис.1 представлены нормированные значения треугольного, трапециевидного и равномерного профилей линейной скорости кровотока, используемых для расчетов формы пульсовой волны.

На рис. 2 и рис.3 представлены результаты расчета зависимости формы пульсового давления при изменении ГДС и податливости стенки артериального русла за время сердечного цикла. Для расчета выбрано стандартное изменение АД от 80 до 120 мм рт.ст. на участке систолы и средние значения ГДС и податливости стенок артериального русла:

Rср= 1,05 мм рт.ст.•с/мл. и Сср = 1,69 мл/мм рт.ст.

На рис.4 представлена расчетная зависимость формы пульсовой волны при треугольном, трапециевидном и равномерном профиле скорости кровотока.

Рис.1 Треугольный, трапециевидный и равномерный профили линейной скорости кровотока, нормированные к среднему значению линейной скорости кровотока

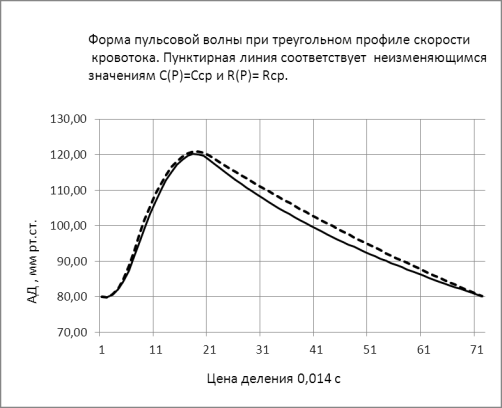
Рис. 2 Форма АД при треугольном профиле скорости кровотока, изменение С равно ±15%, изменение R равно ±12,5%, к средним значениям величин (сплошная линия). Изменение АД за время систолы в диапазоне

80÷120 мм рт.ст.

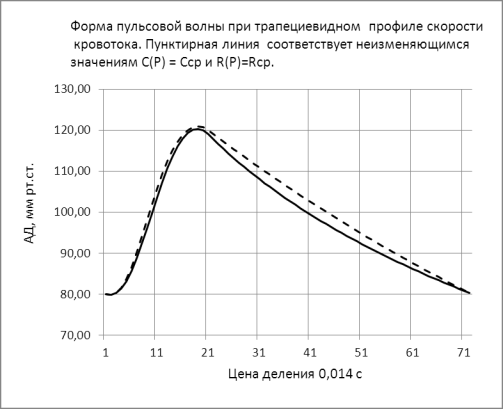
Рис.3 Рис. 3 Форма АД при трапециевидном профиле скорости кровотока, изменение С равно ±15%, изменение R равно ±12,5%, к средним значениям величин (сплошная линия). Изменение АД за время систолы в диапазоне 80÷120 мм рт.ст.

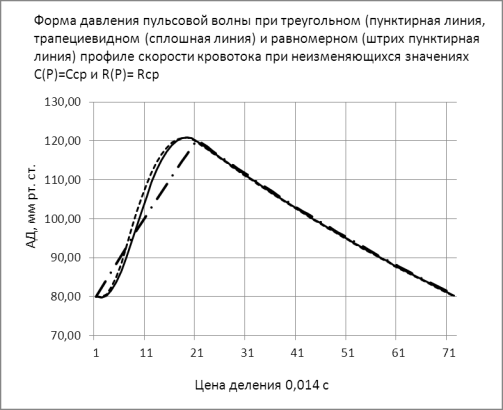
Рис.4 Форма АД при треугольном (пунктирная линия) и трапециевидном (сплошная линия) и равномерном профиле скорости кровотока. С = 1,69 мл/мм рт.ст., R = 1,05 мм рт.ст.•с/мл. Изменение АД за время систолы 80÷120 мм рт.ст.

В литературе отмечается, что в конце систолы наблюдается обратный кровоток в сердце до момента закрытия аортальных клапанов. Величина обратного кровотока по объёму вытолкнутой крови может составлять до 25%.[4].

На рисунке 5 представлены нормированные значения трапециевидного и треугольного профилей линейной скорости кровотока с наличием участка обратного кровотока, используемых для расчетов формы пульсовой волны. На рис.6 представлены рассчитанные формы пульсовой волны для профилей скорости кровотока, представленных на рис. 5.

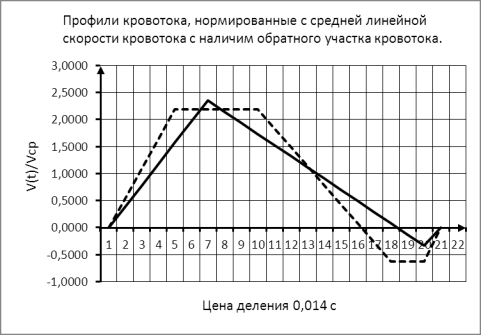
Рис.5 Профили кровотока, нормированные к средней линейной скорости кровотока

У треугольного профиля объем обратного кровотока принят 2,5 % к прямому.

У трапециевидного профиля объём обратного кровотока принят 12 % к прямому.

Рис.6 Расчет формы пульсовой волны для треугольного (сплошная линия) и трапециевидного профилей скорости кровотока при наличии обратного кровотока в конце систолы. Изменение С(Р)составляет ±15% от среднего значения, изменение R(P) составляет ±12,5% от среднего значения.

Из рисунка 6 видно, что с увеличением обратного кровотока, при постоянном ударном объеме, наблюдается более значительное повышение давления по сравнению со значениями при отсутствии обратного кровотока, что позволяет объяснить почему в литературе встречаются разные оценки ударного объема при давлении в организме 120/80 и гидродинамическом сопротивлении 1,06 мм рт.ст с/мл.

Временную зависимость мощности, развиваемой сердцем во время систолы, можно подсчитать на основании выражения [3, стр. 129]:

N(t) = Qv(t)•[P(t) + V(t)²•ρ/2] (21)

где:

Р(t) – артериальное давление, [Па],

Qv – объёмная скорость кровотока [м³/с]/

V(t) – линейная скорость кровотока не превышает 0,5÷0,6, [м/с]/

ρ – плотность крови, [кг/м³]/

Вторым слагаемым в скобках выражения (21) при U(t)=0,6 м/с, плотности крови 1,06 10³ кг/м³, артериальном давлении 100 мм рт.ст можно пренебречь по сравнению с величиной первого слагаемого, которое составляет, примерно 1/70, поэтому, с учетом изменения скорости кровотока за время систолы, выражение (21) будет выглядеть:

N(t) = (Vo/t₁)•(V(t)/Vср)•P(t) (22)

где:

Vo – ударный объем, м³,

t₁ – время систолы, с,

V(t)/Vср - значение линейной скорости кровотока, нормированное к средней скорости кровотока из сердца.

Подставляя в (22) значения для каждого интервала разбиения участка систолы можно вычислить временную зависимость мощности, развиваемой сердцем.

Работа, совершаемая сердцем за время систолы, определится из выражения

t₁

А = ∫ N(t)•dt

0

Расчеты показывают, что максимум мощности при треугольном профиле скорости кровотока соответствует максимуму скорости кровотока, а при трапециевидном профиле максимум соответствует окончанию плоской вершины скорости кровотока. При равномерном истечении скорости кровотока из сердца максимум мощности соответствует окончанию систолы. В таблице 4 приведены результаты расчета максимальной мощности, развиваемой сердцем для различных профилей скорости кровотока и значения энергии, затрачиваемой сердцем на выброс ударного объема крови.

Таблица 4

Профиль скорости кровотока	Без обратного кровотока (рис.1)			С обратным кровотоком (рис.5)
	Треугольный	Трапециевидный	Равномерный	Треугольный	Трапециевидный
Максимальная мощность [Вт]	7,85	7,36	5,13	9,52	10,72
Затрачиваемая энергия, [Дж]	1,24	1,23	1,22	1,26	1,41

Выводы:

1. Показано, что вклад основных артерий, кроме аорты, в совокупную среднюю податливость стенок артериального русла составляет примерно 11%.

2. Показано, что вклад многочисленных артерий, кроме БА, ПА, ОСА, и артериол, в суммарную податливость стенок артериального русла соизмерим с вкладом аорты.

3. Учет нелинейности податливости стенок артериального русла и ГДС оказывает влияние на форму пульсовой волны только на участке диастолы, а на форму пульсовой волны на участке систолы практически не влияет.

4. Показано, что при равномерном выбросе крови за время систолы сердцу необходимо развивать наименьшую мощность.

5. Затрачиваемая энергия на выброс за сердечный цикл, практически не зависит от профиля скорости кровотока из сердца при отсутствии обратного кровотока.

6. Учет обратного кровотока во время сердечного выброса показывает, что развиваемая сердцем мощность становится больше, увеличивается также работа, которую совершает сердце за время систолы.

7. При наличии обратного кровотока максимум артериального давления наступает намного раньше окончания систолы, увеличивается так же значение систолического артериального давления.

Орлов Александр Сергеевич, г Екатеринбург, Orloveburg@rambler.ru.

Список литературы к статье 2.1

1. Мельникова Л.В., Бартош Ф.Л., Бартош Л.Ф. «Структурно-функциональные изменения стенки общих сонных и плечевых артерий при гипертонической и ишимической болезни сердца», Кардиология №9, 2009 г.

2. Орлов А.С. «К вопросу об эквивалентной схеме большого круга кровообращения». Российский журнал Биомеханики. Пермь 2010 г, Том 14, № 3 (43), стр. 47-56.

3. Парашин В.Б., Иткин Г.П. « Биомеханика кровообращения» Издательство МГТУ имени Н.Э. Баумана, 2005 г.

4. Педли Т. «Гидродинамика крупных кровеносных сосудов» пер с англ. М, Мир, 1983 г.

5. Савицкий Н.Н. «Биофизические основы кровообращения и клинические методы изучения гемодинамики». Ленинград «Медицина» Ленинградское отделение, 1974 г.

6 Физиология человека. Под редакцией Р Шмидта и Г. Тевса, Москава. Мир 2007 г.