Технические
науки/2. Механика
Магистрант. Танжарикова
Г.П.
Казахский Национальный Технический
Университет имени К.И. Сатпаева, Казахстан
Определение кинематических параметров шестизвенного шарнирного механизма
четвертого класса
Рассмотрим двухопорный шестизвенный шарнирный механизм четвертого класса.
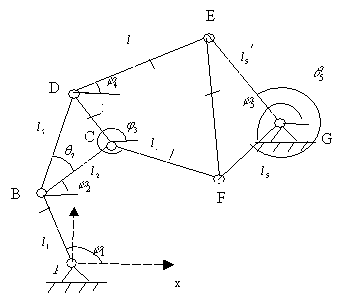
Рис.1 Двухопорный
шестизвенный
шарнирный механизм четвертого класса
Считая положение звеньев известными
определим скорости и ускорения точек рассматриваемого механизма.
Определим число степеней свободы
исследуемого механизма
![]()
Механизм имеет одну степень свободы.
Из векторных уравнений замкнутости двух
независимых контуров для механизма четвертого класса (рис. 1)
![]()
![]()
(1)
![]()
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Путем дифференцирования по обобщенной
координате ![]() можно получить
систему линейных уравнений для определения аналогов скоростей звеньев.
можно получить
систему линейных уравнений для определения аналогов скоростей звеньев.
![]() (2)
(2)
где ![]() .
.
Проектируем равенство (1) по оси x, y
![]()
![]()
![]() (3)
(3)
![]()
Дифференцируем по ![]() :
:

![]() (4)
(4)

![]()
Составим матрицу
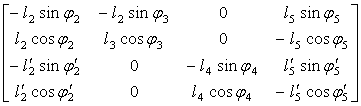 .
.  =
= 
Нач.условия: ![]() ,
, ![]() ,
, ![]() ,
, ![]() где
где ![]() ,
, ![]() ,
, ![]() .
.
Из системы линейных уравнений (4) по
правилу Крамера находим аналоги угловых скоростей звеньев группы
 (i =
2, 3, 4, 5) где
(i =
2, 3, 4, 5) где ![]() и
и ![]() - определители. (5)
- определители. (5)
Определитель ![]() системы (4) представляет собой якобиан исходной
системы уравнений (3) и выражается формулой
системы (4) представляет собой якобиан исходной
системы уравнений (3) и выражается формулой
![]() =
=  (6)
(6)
или
![]() =
= ![]() (7)
(7)
Определитель ![]() получается при замене i-го столбца
в определителе (6) на столбец правых частей уравнений (4).
получается при замене i-го столбца
в определителе (6) на столбец правых частей уравнений (4).
![]() =
=  (8)
(8)
или
![]() =
= ![]() (9)
(9)
Аналог угловой скорости звена 2
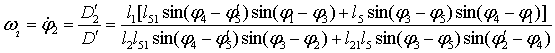 (10)
(10)
![]() =
=  (11)
(11)
или
![]() =
= ![]()
![]() (12)
(12)
Аналог угловой скорости звена 3
![]()
 (13)
(13)
![]() =
= 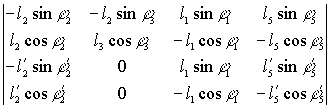 (14)
(14)
или
![]() =
= ![]()
![]() (15)
(15)
Аналог угловой скорости звена 4

 (16)
(16)
![]() =
= 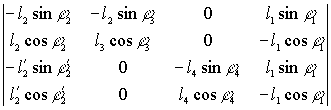 (17)
(17)
или
![]() =
= ![]() (18)
(18)
Аналог угловой скорости звена 5
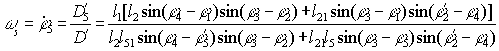 (19)
(19)
Таким образом, найдены угловые скорости,
т.е. ![]() . Угловые ускорения находятся, дифференцируя (4) по
. Угловые ускорения находятся, дифференцируя (4) по ![]() :
:

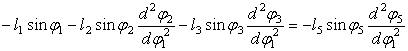 (20)
(20)


Составим матрицу
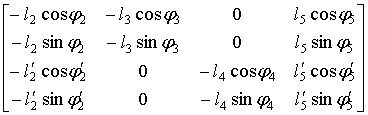 .
.  =
= 
Из системы линейных уравнений (20) можно
найти аналоги угловых ускорений звеньев группы
 (i =
2, 3, 4, 5) где
(i =
2, 3, 4, 5) где ![]() и
и ![]() - определители. (21)
- определители. (21)
![]() =
=  (22)
(22)
или
![]() =
= ![]() (23)
(23)
Определитель ![]() получается при замене i-го столбца
в определителе (22) на столбец правых частей уравнений (20).
получается при замене i-го столбца
в определителе (22) на столбец правых частей уравнений (20).
![]() =
=  (24)
(24)
или
![]() =
= ![]() (25)
(25)
Аналог углового ускорения звена 2
![]() (26)
(26)
![]() =
=  (27)
(27)
или
![]() =
= ![]()
![]() (28)
(28)
Аналог углового ускорения звена 3
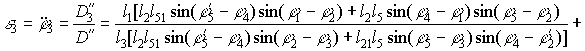
![]() (29)
(29)
![]() =
= 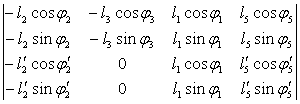 (30)
(30)
или
![]() =
= ![]()
![]() (31)
(31)
Аналог углового ускорения звена 4

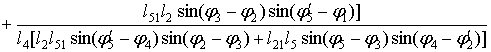 (32)
(32)
![]() =
=  (33)
(33)
или
![]() =
= ![]() (34)
(34)
Аналог углового ускорения звена 4
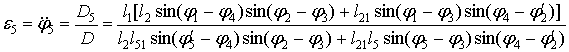 (35)
(35)
По
известным значениям скоростей и ускорений внешних шарниров группы Ассура, а
также угловых скоростей и угловых ускорений звеньев механизма, легко
определяются скорости и ускорения внутренних шарниров группы.
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Полученные зависимости позволяют
определить линейные скорости и ускорения шарнирных точек механизма и угловые
скорости и ускорения его звеньев.
Литература:
1.
Джолдасбеков У.А. Теория механизмов высоких классов. -
Алматы: Гылым, 2001. - 428 с.
2.
Левитский Н.И. Теория
механизмов и машин. – М.: Наука, 1990. – 592с.
3. Пейсах Э.Е. Система оптимизационного кинематического
синтеза рычажных механизмов. – В кн. : Теория механизмов
и машин. Харьков, 1984, вып.37, с.3-8.