К.т.н. доцент Василенко В.С., Василенко М.Ю., Чунарьов А.В.

Національний авіаційний університет (НАУ), Україна

Визначення реальної надлишковості для коду “зважених груп”

Вступ. При виборі завадостійких кодів чи найважливішим є питання щодо надлишковості, якої потребує той чи інший код? Відомі дослідження, наприклад, [1], в яких розглядається оптимальна надлишковість у вигляді потрібної кількості надлишкових символів k_н для базового кодового слова із загальною кількістю символів n. Постає питання: якою буде надлишковість, яка досягається при застосуванні конкретного коду, зокрема коду “зважених” груп, тобто при визначенні реального значення k?

Постановка задачі. Зрозуміло, що для визначення реального значення k_р, необхідно і достатньо знати найбільше значення контрольної ознаки R(A).

Тоді реальне значення кількості символів k контрольної частини R(A) будемо знаходити формулою як функцію:

. (1)

В [2] i [3] було показано, що R(A) знаходиться за формулою:

, (2)

де m - кількість символів в інформаційній частині, - вагові коефіцієнти розрядів інформаційних частин, - інформаційні символи.

Визначення надлишковості для коду “зважених груп”. Як відомо, в двійковій системі числення двійкове число представляється як послідовність нулів і одиниць. Отже може приймати значення або 0 або 1. Контрольна частина R(A) прийме максимальне значення тільки тоді, коли кожний елемент інформаційної частини дорівнює , бо 1 - найбільше число в двійковій системі числення.

Таким чином, виходячи з цих міркувань, вираз (2), необхідний для визначення в подальшому реальних кодів набуде вигляду:

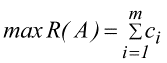(3)

В [2] і [3] було визначено правило вибору вагових коефіцієнтів: вагові коефіцієнти розрядів інформаційних частин мають бути більшими ніж основа системи числення р та не повинні дорівнювати величині pⁱ (і = 0, 1, 2, …), в той час як вагові коефіцієнти контрольних символів повинні дорівнювати величині pⁱ.

Вагові коефіцієнти розрядів інформаційних частин c_i в двійковій системі числення будуть дорівнювати: 3, 5, 6, 7, 9, 10, 11, … . Тобто дорівнюють усім числам, окрім 2ⁱ (і = 0, 1, 2, …, k-1). Отже сукупність вагових коефіцієнтів інформаційних та контрольних розрядів можна вважати такою, що утворює ряд натуральних чисел від 0 до n.

Для знаходження суми вагових коефіцієнтів інформаційної частини коду використаємо той факт, що вона дорівнює сумі усіх вагових коефіцієнтів за виключенням суми вагових коефіцієнтів контрольних розрядів. Окрім того, врахуємо, що перша із цих сум є сумою членів арифметичної прогресії від 1 до n із різницею, що дорівнює 1, а друга є сумою членів геометричної прогресії від 1 до із знаменником 2. Тоді:

Тоді вираз (3 можна переписати у наступному вигляді:

(4)

Функція f у виразі (1) є логарифмічною за основою p, яка для двійкової системи дорівнює 2.

Таким чином, для розробленого коду вираз (1) набуде наступного вигляду:

. (5)

Звернемо увагу, що шукане значення знаходиться в обох частинах нерівняння (5).

З нерівності (5) знайдемо вираз для розрахунку нижньої межі реально потрібної розрядності контрольної ознаки для коду, що розглядається, . Для цього здійснимо наступну низку перетворень.

, (6)

,

,

.

Таким чином, нижня межа реально потрібної розрядності контрольної ознаки для коду, що розглядається, може бути визначеною із нерівності:

. (7)

Верхню межу реально потрібної розрядності контрольної ознаки для коду, що розглядається, можна знайти шляхом аналізу підлогарифмічного виразу в нерівності (6), значення якого не може бути від’ємним. Отже, після низки наступних перетворень:

,

,

,

,

одержимо вираз для визначення шуканого значення верхньої межі реально потрібної розрядності контрольної ознаки для коду, що розглядається:

(8)

При визначенні реально потрібної розрядності контрольної ознаки для коду, що розглядається, слід враховувати, що ця величина може приймати лише цілочисельне значення. Тоді в виразах (7) та (8) замість можливих дробових значень логарифмів слід використовувати їх найближче більше ціле, наприклад здійснювати перехід типу (стосовно виразу (7)):

.

В цій формулі [X] – означає обчислення цілої частини від Х.

Результати розрахунків за виразами (7) та (8) зведено в порівняльну таблицю.

n	4	5	6	7	8	12	16	24	32	40
kн	3	3	3	3	4	4	5	5	6	6
min kP	2	3	3	4	4	5	6	7	8	9
max kн	3	3	4	4	5	6	7	8	9	9

n	48	56	64	80	96	112	128	144	160	176
kн	6	6	7	7	7	7	8	8	8	8
min kP	9	10	10	11	11	12	13	12	13	13
max kн	10	10	11	11	12	12	13	13	13	13

n	192	208	224	240	256
kн	8	8	8	8	9
min kP	13	13	14	14	14
max kн	14	14	14	14	15

Висновки. Одержані результати дозволяють стверджувати, що надлишковість, якої потребує код “зважених груп” при малих розрядностях БКС (n) не перевищує оптимальної, а в разі збільшення розрядності БКС (n) є несуттєво більшою за оптимальну.

ЛІТЕРАТУРА:

1. К.т.н. доцент Василенко В.С., Василенко М.Ю., Чунарьов А.В. Визначення потрібної надлишковості в коді “Зважених груп”. Оптимальна надлишковість. Тези доповіді 6-ої міжнародної науково–практичної конференції "АKTUÁLNÍ VYMOŽENOSTI VĚDY - 2010", Dĺl 14, 27.06.2010 - 05.07.2010, ст. 22-24.

2. Василенко М. Ю., Чунарьов А.В. Вибір вагових коефіцієнтів в коді “Зважених груп”. Тези доповіді 5-ої міжнародної науково–практичної конференції «ZPRÁVY VĚDECKÉ IDEJE - 2009», Dĺl 12, 27.10 - 05.11.2009, ст. 33-36.

3. Василенко М.Ю., Чунарьов А.В. Вимоги щодо вагових коефіцієнтів в коді “зважених груп”. Strategiczne pytania swiatowej nauki – 2010: тези доповіді 5-ої міжнародної науково-практичної конференції – Przemysl: Nauka i studia, 2010. – Vol. 14.– С.84-86.