Математика / 5. Математическое моделирование

К.ф.-м.н. Мищенко В.В., д.ф.-м.н. Сандраков Г.В.

Национальный авиационный университет, Киев, Украина

Киевский национальный университет им. Т. Г. Шевченко, Украина

Численное моделирование токопроводящих свойств плазмы

Рассматривается процесс электродинамического разгона макротел с помощью металлического якоря в канале прямоугольного сечения. За счет трения происходит процесс испарения металла якоря с его задней поверхности. Поскольку возникающее при этом плазменное облако обладает токопроводящими свойствами, то представляется возможным при некоторых режимах замыкание электрической цепи металлического якоря областью токопроводящей плазмы. В работе рассматривается математическая модель и алгоритм численного расчета параметров указанного процесса.

Движение якоря моделируется с учетом испарения металла с его задней кромки. Задача решается в два этапа. На первом этапе определяется скорость движения тела и определяется время скин-горения задней кромки металлического тела из системы уравнений

,

,

.

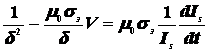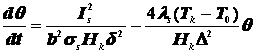где - эффективный размер прохождения тока через контактную границу между телом и электродом, , - электропроводность материала рельсов и тела соответственно, - теплопроводность тела, - температура кипения тела, - начальная температура, - размер области прогрева током в окрестности угла задней кромки тела, - теплосодержание единицы массы тела при кипении, , - температура тела в углу задней кромки. После того, как достигло значения 1, начинается испарение материала тела в окрестности задней кромки тела.

На втором этапе моделируются процессы в образовавшемся плазменном облаке. Для их определения используются уравнения газовой динамики для области плазмы в двумерном случае

, (1)

, (2)

, (3)

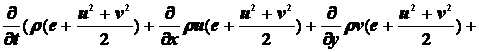
, (4)

где компоненты скорости по и соответственно, - давление, -плот-ность, внутренняя энергия, индукция магнитного поля.

Эти уравнения рассматриваются совместно с уравнениями для магнитного поля в плазме, электродах и металлическом теле:

, (5)

, (6)

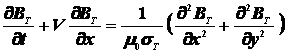, (7)

где -скорость движения тела, - индукция магнитного поля в плазме, электродах и металлическом теле соответственно.

Граничные условия в области течения пара имеют вид:

при ,

где 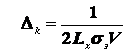обозначает ширину зоны испарения металла,

при ,

при : ,

где обозначает координату фронта области, заполненной паром. Особенностями задачи является наличие притока массы через границы области и изменение во времени границ области плазмы. Алгоритм численного расчета газодинамических параметров построен на основе метода крупных частиц без введения искусственной вязкости [1]. Для этого система сначала приводится к дивергентному виду

,

, ()

, ()

, ()

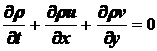где

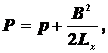
Для численного решения прямоугольная область разбивается эйлеровой сеткой на ячейки с постоянными шагами по пространственным переменным. На первом этапе производится расчет потоков массы, импульса и энергии по формулам первого порядка точности, а внешние притоки учитываются на заключительном этапе метода. Ячейки, в которых плотность имеет достаточно малые значения, считается пустыми.

При решении системы уравнений Максвелла (5)-(7) вместо трех уравнений рассматривается одно уравнение в совмещенной области, но с разрывным коэффициентам :

.

При таком подходе в качестве решения понимается обобщенное решение в смысле интегрального тождества. Для расчета уравнений Максвелла использовалась неявная разностная схема на пятиточечном шаблоне. Для решения возникающей системы разностных уравнений использовался итерационный процесс [2], устойчивый к разбросу значений коэффициентов.

Литература:

1. Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике. Вычислительный эксперимент. М.: Наука, 1982.

2. Бахвалов Н.С., Богачев К.Ю., Maitre J.F. Эффективный алгоритм решения жестких эллиптических задач с малым параметром с приложениями к методу фиктивных областей. ЖВМ и МФ 39 (1999), № 12, с. 2017-2046.