Технические науки / 2. Механика

к. техн. наук Обухов А.Н., Дмитренко И.С.

Донбасская государственная машиностроительная академия

Об ударных колебаниях упругого шарика, движущегося под действием силы сопротивления, пропорциональной квадрату скорости (амплитудная характеристика)

Постановка задачи: Упругий шарик, массой m падает с высоты H₀ и ударяется об упругую плиту. Требуется найти закон дальнейшего движения шарика, если известно, что сила сопротивления пропорциональна квадрату скорости с коэффициентом пропорциональности k (коэффициент восстановления при ударе шарика о плиту ).

Решение поставленной задачи разобьем на три этапа.

Первый этап. Движение шарика вниз до удара о плиту, нахождение скорости удара о плиту.

Второй этап. Движение шарика вверх с заданной скоростью (скорость, с которой шарик отскочит от плиты), нахождение наибольшей высоты подъема.

Третий этап. Дальнейшее движение шарика (повторные удары), вывод рекуррентной формулы амплитуды колебаний шарика в зависимости от числа ударов.

Решение.

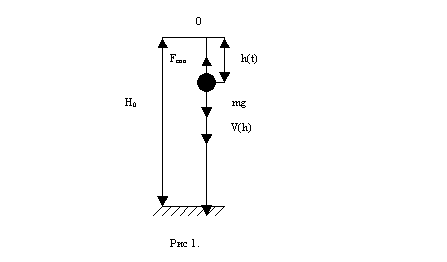
Расчетная схема для вывода дифференциального уравнения движения шарика см. рис. 1.

Обозначим через - соответственно путь и скорость шарика в момент времени .

Можно показать, что дифференциальное уравнение движения шарика на первом этапе имеет вид:

, где (1)

Решение уравнения (1), удовлетворяющее начальным условиям, при имеет вид:

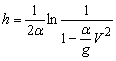(2)

Полагая в равенстве (2) , найдем скорость, с которой шарик ударяется о плиту

(3)

При ударе о плиту шарик мгновенно теряет направление скорости на противоположное, величина которой равна . Величину этой скорости будем считать начальной скоростью на втором этапе движения шарика.

Расчетная схема движения шарика см. рис. 2.

Дифференциальное уравнение движения на втором этапе имеет вид:

(4)

Решение уравнения (4), удовлетворяющее начальным условиям имеет вид:

(5)

Полагая в равенстве , найдем наибольшую высоту подъема шарика

(6)

Учитывая, что

(7)

Найдем наибольшую высоту подъема шарика при первом ударе

(8)

Повторяя выше изложенное, найдем формулу для вычисления наибольшей высоты подъема шарика при втором ударе

(9)

И, наконец, рекуррентная формула наибольшей высоты (амплитуды) подъема шарика при n-м ударе имеет вид:

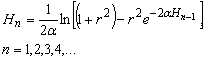(10)

Проанализируем выражение, стоящее под знаком логарифма, учитывая выражение (10), получим:

цепную дробь вида:

Найдем сумму этой периодической дроби при . Пусть сумма этой дроби при равна числу p. Тогда, учитывая вид дроби, запишем равенство , отсюда

Решая уравнение, найдем

Проанализируем поведение амплитуды колебаний при .

, с возрастанием числа ударов, амплитуда колебаний уменьшается и стремится к нулю. Второй корень уравнения не подходит по физическому смыслу, так как

Оценим порядок стремления к нулю амплитуды колебаний шарика в зависимости от числа ударов. Преобразуем выражение (10), отбросив слагаемые выше :

Получим, что (11)

Рассмотрим соотношение

Полагая , получим дифференциальное уравнение для :

(12)

Пусть r=1, тогда или

Интегрируя правую и левую части равенства, получим . Найдем H_k , используя условие: при (*) в виде

(13)

Пусть r<1, тогда пренебрегая в (12) вторым слагаемым, , и решение имеет вид:

(14)

Используя условие (*), получим зависимость в виде

(15)

Анализируя выражения (13),(15), заключаем, что в случае абсолютно упругого удара r=1, амплитуда колебаний убывает по гиперболическому закону (достаточно медленно), а в случае упругого удара с коэффициентом восстановления , амплитуда колебаний убывает по экспоненте (достаточно быстро).

Вывод. Поставлена и решена задача о существенно нелинейных ударных колебаниях упругого шарика, движущегося под действием силы сопротивления пропорциональной квадрату скорости движения. Получена (10)рекуррентная формула амплитуды колебаний в зависимости от числа ударов шарика. Показано, что с ростом числа ударов амплитуда колебаний убывает в случаях абсолютно упругого удара о плиту по гиперболическому закону (13), упругого удара с коэффициентом восстановления по экспоненте (15).