Твердохлебова С.В.

Днепропетровский национальный университет. Днепропетровск. Украина.

ОПТИЧЕСКИЕ ИССЛЕДОВАНИЯ СПЛАВОВ С КВАЗИКРИСТАЛЛИЧЕСКОЙ СТРУКТУРОЙ

Квазикристаллические материалы относят к классу металлических высокорезистивных сплавов [1]. В отличие от металлов их электросопротивление при низких температурах аномально велико [2]. Однако с ростом температуры оно уменьшается [2]. Но, несмотря на этот факт, оно все-таки превышает электросопротивление чистой меди примерно на 3 порядка [1]. Последнее, по-видимому, означает, что металлическая связь исходных металлов претерпевает существенное изменение при их сплавлении. Исходя из этого, можно полагать, что определяющим параметром свойств квазикристаллов, в частности электрических, является концентрация свободных носителей заряда. В связи с этим представляет интерес проведение оптических исследований сплавов с квазикристаллической структурой.

В работе использованы сплавы с кристаллической структурой систем Al-Fe₂₀, Al-Cu₂₁ и сплавы составов Al₆₂-Cu_24,5-Fe_13,5 и Al₆₄-Cu₂₂-Fe₁₄ содержащие 50% квазикристаллической фазы. Химический состав сплавов находили методом рентгенофлуоресцентного анализа. Поскольку друдевская составляющая от свободных носителей в спектрах квазикристаллов не наблюдается [1], для нахождения концентрации свободных электронов привлекали метод оптической спектроскопии плазмы.

Основой проведения эксперимента были базовые тезисы, заключающиеся в том, что, во-первых, скорость поступления вещества в плазму разряда коррелирует с теплофизическими свойствами материала [3]. Во-вторых, изменение поступления материала в плазму разряда оказывает существенное влияние на условия возбуждения [3] и, естественно, на характеристики плазмы. Параметрами плазмы выступали температура возбуждения и концентрация свободных электронов. Температуру возбуждения Т_в определяли методом Л. С. Орнштейна, основанным на измерении относительных интенсивностей пары спектральных линий, принадлежащих одному элементу. Такие пары называют термометрическими. В качестве термометрических пар были использованы спектральные линии цинка и железа: ZnI 307,6 нм - ZnI 328,2 нм; FeI 323,3 нм - FeI 317,8 нм. Ниже приведено общее выражение [4] для расчета температуры возбуждения (1):

Т_в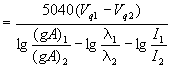 (1),

где V_q1 и V_q2 - потенциалы возбуждения спектральных линий; (gA)₁ и (gA)₂ -произведение статистического веса возбужденного состояния на вероятность излучательного перехода для спектральных линий 1 и 2; l₁ и l₂ - длины волн спектральных линий термометрической пары; I₁ и I₂ - относительные интенсивности спектральных линий 1 и 2. Подставив в уравнение (1) атомные постоянные, получим рабочие формулы (2) и (3) для термометрических пар спектральных линий цинка (2) и железа (3):

Т_в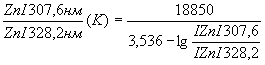[4] (2)

Т_в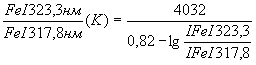 (3)

Относительное стандартное отклонение при определении температуры возбуждения составляло 2,0 %. Концентрацию свободных электронов N_e в 1 см³ плазмы измеряли с привлечением термометрической пары спектральных линий магния : MgII 279,55 нм -MgI 285,21 нм по рабочей формуле (4):

[4], (4)

где –электронное давление, пропорциональное N_e [4], ,-относительные интенсивности искровой и дуговой линий магния, - температура возбуждения. Погрешность определения электронного давления составляла 10% – 15%. В таблице 1 показаны значения температуры возбуждения и давления свободных электронов в 1 см³ плазмы для исследуемых сплавов. Там же приведены значения Т_в и p_e для чистых металлов – меди, алюминия и железа, взятые из литературных источников.

Таблица 1

Температура возбуждения Т_в, давление свободных электронов p_e в 1 см³ плазмы дугового разряда и относительные значения плазменной частоты для исследуемых сплавов

Система сплава	Тв, К	ре×10^5, атм
Al-Fe20	5270	12,9	-
Al-Cu21	5200	10,4	-
Al62,5-Cu25-Fe12,5 [1]	-	-	0,61 [1]
Al62-Cu24,5-Fe13,5	5070	5,52	0,55
Al64-Cu22-Fe14	5040	5,85	0,58
Cu	5160[5]	16,9 [5]	-
Al	5000[4]	13,6 [4]	-
Fe	5500[6]	22,5 [6]	-

Анализ данных таблицы 1 свидетельствует о том, что давление свободных электронов в 1см³ плазмы, содержащей пары¢ сплавов с квазикристаллическими фазами составов Al₆₄-Cu₂₂-Fe₁₄ и Al₆₂-Cu_24,5-Fe_13,5 , в 2-3 раза ниже такого, как для чистых металлов: меди, железа и алюминия, так и для кристаллических сплавов Al-Fe₂₀, Al-Cu₂₁. Поскольку давление свободных электронов измерено в плазме, интересно проследить за существованием зависимости концентрации свободных электронов в твердом теле, выраженной через световую проводимость с доминирующим внутризонным вкладом, от концентрации носителей заряда в плазме на кристаллических сплавах.. Величины оптической проводимости, обусловленной вкладом свободных электронов, заимствовали из работ [7,8]. Значения световой проводимости определены на частоте 0,10 эв. На рис.1 представлена зависимость давления свободных электронов в 1 см³ плазмы от световой проводимости в твердом теле.

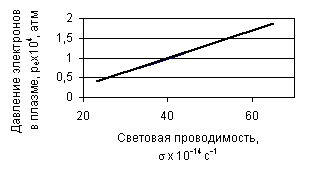
Рис.1. Зависимость давления свободных электронов в плазме, р_е, от световой проводимости, s, в твердом теле

Корреляционный анализ такой зависимости показал коэффициент корреляции 0.988 при r- распределении (на уровне значимости 0,05) 0,521. Результаты корреляционного анализа позволяют считать, что величина давления свободных электронов, а, следовательно, и концентрации носителей заряда в 1 см³ плазмы, может служить параметром для характеристики концентрации свободных электронов в твердом теле. Отсюда появилась возможность вычисления плазменной частоты, ², которая определяется особенностями электронно-энергетического спектра на уровне Ферми [7]. В приближении свободных электронов плазменная частота описывается выражением [7]:

, (5)

где – заряд и масса свободного электрона, – концентрация электронов проводимости. Причем, при расчете ² в значения нами был введен поправочный коэффициент 0,4 ×10⁸, найденный из линейной зависимости литературных данных концентрации свободных электронов в твердом теле от концентрации носителей заряда в плазме. В таблице 1 приведены относительные значения плазменной частоты , где ² – плазменная частота сплава с квазикристаллической структурой, - плазменная частота сплава с кристаллической структурой.Причем, эта величина для совершенного квазикристалла Al_62,5-Cu_25,0-Fe_12,5 [1] отражает степень деформации исходной зоны проводимости, так как авторами [1] установлено, что совершенный квазикристалл Al_62,5-Cu_25,0-Fe_12,5 имеет деформированную исходную зону проводимости. Найденное нами снижение электронного давления в 1 см³ плазмы для исследуемых сплавов примерно в 3 раза по сравнению с таким для чистых металлов означает, что металлическая связь исходных металлов претерпевает существенное изменение при сплавлении. Это изменение проявляется, по-видимому, в деформации исходной зоны проводимости квазикристаллических фаз исследуемых сплавов, поскольку относительные величины их плазменных частот (табл.1) близки к значению 0,61, то есть к степени деформации исходной зоны проводимости для совершенного квазикристалла.

Литература

[1] Прекул А.Ф., Номерованная Л.В., Рольщиков А.Б., Щеголихина Н.И., Ярцев С.В. Особенности электропроводности и оптического поглощения в ультравысокорезистивном квазикристаллическом сплаве Al_62,5-Cu_25,0-Fe_12,5. / Физика металлов и металловедение. 1996. Т.82. Вып. 5. С. 75-82.

[2] Гратиа Д. Квазикристаллы. // Успехи физических наук. 1988. Т.156. Вып. 2. С. 347-363.

[3] Методы спектрального анализа металлов и сплавов. ( Ю.М.Буравлев, И.А.Грикит, О.И.Никитина и др.) К.: Тэхника. 1988. 215с.

[4] Boumans P.W. Theory of spectrochemical excitation. New York: Plenium Press. 1966. 368p.

[5] Корлисс Ч., Бозман И. Вероятности переходов и силы осцилляторов 70 элементов. М.: Атомиздат. 1968. 627с.

[6] Русанов А.К. Основы количественного спектрального анализа руд и минералов . М.: Недра. 1978. 400с.

[7] Афанасьева Л.А., Кириллова М.М., Носков М.М. Оптические и магнитооптические свойства железа. //ФММ. 1966. Т.21. С. 288-293.

[8] Livjenvall H.G. Optical properties of aluminium alloys. || Solid State Commun. 1971. V.9. P. 169-179.