Математика/1.
Диференцiальнi та iнтегральнi рiвняння
Городецький В.В., Колiсник
Р.С.
Чернiвецький нацiональний унiверситет iменi Юрiя Федьковича
Властивостi фундаментального розв’язку задачi Кошi для
одного класу еволюцiйних рiвнянь з оператором диференцiювання нескiнченного
порядку
Дана робота є продовженням [1,2], в яких
побудованi класи цiлих функцiй (простори типу ![]() ), якi спадають
на дiйснiй вiсi при
), якi спадають
на дiйснiй вiсi при ![]() швидше, нiж
швидше, нiж ![]() , при цьому простори типу
, при цьому простори типу ![]() , побудованi I.М.Гельфандом i Г.Є.Шиловим, а також простори типу
, побудованi I.М.Гельфандом i Г.Є.Шиловим, а також простори типу ![]() , введенi Б.Л.Гуревичем, утворюють
певнi пiдкласи просторiв типу
, введенi Б.Л.Гуревичем, утворюють
певнi пiдкласи просторiв типу ![]() ; знайдено
необхiднi й достатнi умови, за яких оператор диференцiювання нескiнченного порядку коректно
визначений i обмежений у просторах
типу
; знайдено
необхiднi й достатнi умови, за яких оператор диференцiювання нескiнченного порядку коректно
визначений i обмежений у просторах
типу ![]() ; дослiджено властивостi перетворення Фур’є основних
та узагальнених функцiй iз просторiв
типу
; дослiджено властивостi перетворення Фур’є основних
та узагальнених функцiй iз просторiв
типу ![]() та
та ![]() , згорток, згортувачiв та мультиплiкаторiв.
, згорток, згортувачiв та мультиплiкаторiв.
Цi результати дають можливiсть розвинути
теорiю задачi Кошi
для еволюцiйних рiвнянь з оператором
диференцiювання нескiнченного порядку i початковими умовами, якi є
узагальненими функцiями типу ультрарозподiлiв. Зокрема, у роботi встановлено оцiнки фундаментального розв’язку
задачi Кошi (функцiї![]()
![]() ), диференцiйовнiсть
(по
), диференцiйовнiсть
(по ![]() ) функцiї
) функцiї ![]() як абстрактної функцiї параметра
як абстрактної функцiї параметра ![]() iз значеннями у
просторах типу
iз значеннями у
просторах типу ![]() та формулу диференцiювання (по
та формулу диференцiювання (по ![]() ) згортки
) згортки ![]() ; iснування граничного
значення вказаної згортки при
; iснування граничного
значення вказаної згортки при ![]() у просторах типу
у просторах типу ![]() , а також знайдено умови, за яких задача Кошi для еволюцiйних
рiвнянь з оператором диференцiювання нескiнченного порядку зi сталими коефiцiєнтами
коректно розв’язна у певних пiдпросторах узагальнених функцiй типу
, а також знайдено умови, за яких задача Кошi для еволюцiйних
рiвнянь з оператором диференцiювання нескiнченного порядку зi сталими коефiцiєнтами
коректно розв’язна у певних пiдпросторах узагальнених функцiй типу ![]() , якi збiгаються з множинами початкових значень гладких
розв’язкiв вказаних рiвнянь.
, якi збiгаються з множинами початкових значень гладких
розв’язкiв вказаних рiвнянь.
1. Простiр ![]() . Розглянемо монотонно зростаючу послiдовнiсть
. Розглянемо монотонно зростаючу послiдовнiсть ![]() додатних чисел таку,
що: 1)
додатних чисел таку,
що: 1) ![]() ,
, ![]() ; 2)
; 2) ![]()
![]()
![]() :
: ![]() ; 3)
; 3) ![]()
![]()
![]() :
: ![]() i покладемо
i покладемо ![]()
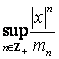 ,
, ![]() ;
; ![]()
![]()
![]() . Функцiя
. Функцiя ![]() – неперервна, парна на
– неперервна, парна на
![]() , монотонно зростає на
, монотонно зростає на ![]() i монотонно спадає
на
i монотонно спадає
на ![]() крiм того,
крiм того, ![]()
![]()
![]() :
: ![]() . За функцiєю
. За функцiєю ![]() будуємо послiдовнiсть
будуємо послiдовнiсть  Встановлено, що: 1)
послiдовнiсть
Встановлено, що: 1)
послiдовнiсть ![]() є монотонно
спадною; 2)
є монотонно
спадною; 2) ![]() ; 3) послiдовнiсть
; 3) послiдовнiсть 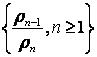 – обмежена зверху.
– обмежена зверху.
Нехай ![]() – зростаюча
послiдовнiсть додатних чисел, яка володiє властивостями 1) – 3). Покладемо
– зростаюча
послiдовнiсть додатних чисел, яка володiє властивостями 1) – 3). Покладемо ![]()

![]()
![]() ;
; ![]()
![]()
![]() . Функцiя
. Функцiя ![]() – невiд’ємна, неперервна, парна на
– невiд’ємна, неперервна, парна на ![]() функцiя, яка монотонно
спадає на
функцiя, яка монотонно
спадає на ![]() i монотонно зростає на
i монотонно зростає на
![]() ; при цьому
; при цьому
![]()
![]()
![]()
![]() .
.
Символом ![]() позначимо сукупнiсть
усiх цiлих функцiй
позначимо сукупнiсть
усiх цiлих функцiй ![]() , якi задовольняють умову
, якi задовольняють умову
![]()
![]()
![]()
![]() :
: ![]() .
.
У просторi ![]() визначенi та є неперервними операцiї множення
на незалежну змiнну, диференцiювання, зсуву аргументу. Для
функцiї j Î
визначенi та є неперервними операцiї множення
на незалежну змiнну, диференцiювання, зсуву аргументу. Для
функцiї j Î![]() еквiвалентними є
наступнi твердження [1]:
еквiвалентними є
наступнi твердження [1]:
1) ![]()
![]() :
: ![]() ;
;
2) ![]()
![]()
![]() :
: ![]() .
.
Зазначимо, що якщо покласти ![]()
![]() , де
, де ![]() – розв’язок рiвняння
– розв’язок рiвняння ![]()
![]() – розв’язок рiвняння
– розв’язок рiвняння ![]() за умови, що
за умови, що ![]() – диференцiйовнi,
невiд’ємнi, парнi на
– диференцiйовнi,
невiд’ємнi, парнi на ![]() , зростаючi i опуклi на
, зростаючi i опуклi на ![]() функцiї, то
простiр
функцiї, то
простiр ![]() збiгається з простором
збiгається з простором
![]() , який вiдноситься до просторiв типу
, який вiдноситься до просторiв типу ![]() , введених Б.Л.Гуревичем.
, введених Б.Л.Гуревичем.
Сукупнiсть функцiй з простору ![]() , звужених на
, звужених на ![]() , позначимо символом
, позначимо символом ![]() .
.
Нехай ![]() – функцiя,
двоïста за Юнгом до функцiï
– функцiя,
двоïста за Юнгом до функцiï ![]() ,
, ![]() ;
; ![]() – функцiя,
двоïста за Юнгом до функцiï
– функцiя,
двоïста за Юнгом до функцiï ![]() ,
, ![]() ,
, 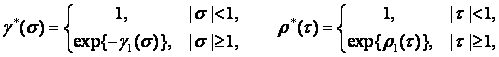
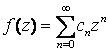 – деяка цiла функцiя.
Говоритимемо, що в просторi
– деяка цiла функцiя.
Говоритимемо, що в просторi ![]() задано диференцiальний оператор нескiнченного
порядку
задано диференцiальний оператор нескiнченного
порядку 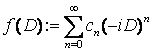 ,
, ![]() , якщо для довiльної основної функцiї
, якщо для довiльної основної функцiї ![]() ряд
ряд ![]()
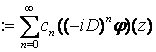 зображає деяку основну
функцiю з простору
зображає деяку основну
функцiю з простору ![]() . У [2] доведено, що якщо цiла функцiя
. У [2] доведено, що якщо цiла функцiя ![]() є мультиплiкатором у
просторi
є мультиплiкатором у
просторi ![]() , то у просторi
, то у просторi ![]() визначений i є неперервним оператор
диференцiювання нескiнченного порядку
визначений i є неперервним оператор
диференцiювання нескiнченного порядку ![]() . Нехай
. Нехай ![]() – звуження оператора
– звуження оператора ![]() на
на ![]() . Тодi для довiльної функцiї
. Тодi для довiльної функцiї ![]()
![]() правильною є рiвнiсть
правильною є рiвнiсть ![]() ,
,![]()
![]() ; тут
; тут ![]()
![]()
![]()
![]() (
(![]() ) – пряме перетворення Фур’є,
) – пряме перетворення Фур’є,
![]()
![]() (
(![]() )
) ![]()
![]() – обернене
перетворення Фур’є.
– обернене
перетворення Фур’є.
2. Еволюцiйнi рiвняння з
оператором диференцiювання нескiнченного порядку у просторах типу ![]() .
.
Розглянемо еволюцiйне рiвняння вигляду
![]() , (1)
, (1)
де
![]() – оператор диференцiювання нескiнченного порядку, побудований за
функцiєю
– оператор диференцiювання нескiнченного порядку, побудований за
функцiєю ![]() у припущеннi, що
у припущеннi, що ![]() – мультиплiкатор у
просторi
– мультиплiкатор у
просторi ![]() i
i ![]() .
.
У
данiй роботi дослiдженi властивостi функцiї G(t, ×):=![]() , яка є фундаментальним розв’язком задачi Кошi для
рiвняння (1).
, яка є фундаментальним розв’язком задачi Кошi для
рiвняння (1).
Основнi результати, одержанi тут, мiстяться в
наступних твердженнях.
Лема 1. Функцiя ![]() при фiксованому
при фiксованому ![]() як функцiя аргумента
як функцiя аргумента ![]() є елементом простору
є елементом простору ![]() ; при цьому
; при цьому
 ,
,
де
![]() ,
, ![]() , t Î (0, T], {s, t} Ì
, t Î (0, T], {s, t} Ì ![]() ,
, ![]() – фiксований параметр.
– фiксований параметр.
Для похiдних функцiї ![]() на дiйснiй вiсi
правильними є нерiвностi
на дiйснiй вiсi
правильними є нерiвностi
 ,
,
де ![]() , s Î
, s Î ![]() , n Î
, n Î ![]() ,
, ![]() , nn(t) –
розв’язок рiвняння
, nn(t) –
розв’язок рiвняння ![]() ,
, ![]() ,
, ![]() , при фiксованому
, при фiксованому ![]() та
та ![]() .
.
Лема 2. Функцiя ![]() ,
, ![]() , як абстрактна функцiя
параметра
, як абстрактна функцiя
параметра ![]() iз значеннями в
просторi
iз значеннями в
просторi ![]() , диференцiйовна по
, диференцiйовна по ![]() , при цьому
, при цьому
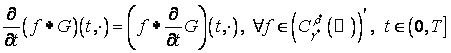 ,
,
де
![]() – простiр топологiчно
спряжений до
– простiр топологiчно
спряжений до ![]() (
(![]() ).
).
Лема 3. Нехай узагальнена функцiя ![]() – згортувач у просторi
– згортувач у просторi
![]() ,
, ![]() . Тодi граничне
спiввiдношення
. Тодi граничне
спiввiдношення ![]() , виконується у просторi
, виконується у просторi ![]() .
.
Лема 3 дозволяє поставити задачу Кошi для рiвняння (1). Задамо початкову умову
![]() , (2)
, (2)
де
![]() – узагальнена функцiя
з простору
– узагальнена функцiя
з простору ![]() . Пiд розв’язком задачi Кошi (1), (2) розумiтимемо розв’язок
рiвняння (1), який задовольняє початкову умову (2) у тому сенсi, що
. Пiд розв’язком задачi Кошi (1), (2) розумiтимемо розв’язок
рiвняння (1), який задовольняє початкову умову (2) у тому сенсi, що ![]() при
при ![]() у просторi
у просторi ![]() .
.
Основний результат роботи складає наступне твердження.
Теорема. Задача Кошi (1),
(2) коректно розв’язна в класi
початкових узагальнених функцiй ![]() ; при цьому
розв’язок подається у виглядi
; при цьому
розв’язок подається у виглядi
![]()
![]() .
.
![]() – сукупнiсть усiх узагальнених функцiй з простору
– сукупнiсть усiх узагальнених функцiй з простору ![]() , якi є згортувачами у просторi
, якi є згортувачами у просторi ![]() .
.
Лiтература:
1. Городецький В.В., Колiсник Р.С. Про одне узагальнення просторiв типу ![]() // Науковий вiсник Чернiвецького унiверситету: Зб. наук. пр.
Вип.134. Математика. – Чернiвцi: Рута, 2002. – С. 30-37.
// Науковий вiсник Чернiвецького унiверситету: Зб. наук. пр.
Вип.134. Математика. – Чернiвцi: Рута, 2002. – С. 30-37.
2. Городецький В.В., Колiсник Р.С. Оператори
диференцiювання нескiнченного порядку у просторах типу ![]() та їх застосування //
Доп. НАН України. – 2004. – № 10. – С. 14–19.
та їх застосування //
Доп. НАН України. – 2004. – № 10. – С. 14–19.