Ершова Н.М.

Приднепровская государственная академия строительства

и архитектуры

РЕШЕНИЕ ЗАДАЧ КОММИВОЯЖЕРА

И ОПРЕДЕЛЕНИЯ КРАТЧАЙШИХ РАССТОЯНИЙ

МЕТОДОМ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Задача коммивояжера (бродячего торговца) заключается в следующем. Имеется несколько пунктов на местности. Требуется найти кратчайший путь их объезда, начиная с некоторого пункта. При этом необходимо объехать все пункты и вернуться в начальный пункт, побывав на каждом пункте только один раз. При полевых работах подобная задача встречается часто и в разных ситуациях: при обследовании объектов и пунктов триангуляции, при рекогносцировке, при выборочном дешифрировании и пр. [1]. Пункты, в которых надо побывать, всегда известны. Уменьшение пути обхода намеченных пунктов экономит время, снижает транспортные расходы и др.

Существует более ста методов решения задачи коммивояжера, в работе [2] задача решена методом ветвей и границ, в работе [5] – методом ближайшего соседа, который, по мнению авторов, наиболее прост. В этой работе отмечено, что методом динамического программирования можно решить задачу с менее 17 пунктами обхода. Это связано с тем, что авторы сами усложнили метод динамического программирования.

Покажем эффективность метода динамического программирования на примере сети дорог, изображенной на рис. 1[1].

В задаче коммивояжера требуется определить две оптимальные траектории, которые соответствуют кратчайшим расстояниям между пунктами при движении от первого пункта ко второму и обратно. При этом следует учесть, что посетить нужно все пункты и только один раз. В качестве целевой функции выступает минимум расстояния между пунктами и . На сети дорог нанесены расстояния между отдельными пунктами в километрах.

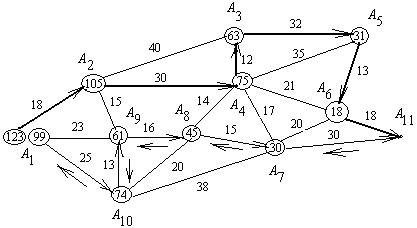
Рис. 1. Сеть автомобильных дорог

Разработка модели. Весь процесс движения от пункта к пункту и обратно можно рассматривать как многошаговый. Каждый шаг представляет собой перемещение из одного пункта сети в другой. Так как пунктов 11, то и шагов 11. Задача состоит в принятии решения на каждом шаге: выбор направления движения из данного пункта в следующий пункт.

Состояние системы характеризуется одним параметром – движение из одного пункта в другой. Процесс является одномерным и легко изображается на плоскости. Пересечение дорог на каждом из шагов соответствует одному из возможных состояний системы (коммивояжера).

Суть выбора оптимальной траектории заключается в следующем. Последний шаг условно спланирован. Действительно, в каком бы из возможных пунктов ( или ) перед пунктом ни оказался коммивояжер, известно, какое решение следует принять. Задачу решаем с конца, т.е. определяем возможные направления движения из пункта к пункту (отмечены стрелками) и отсекаем невозможные направления движения. В кружках на сети указывается значение критерия оптимальности с нарастающим итогом, причем в случае нескольких возможных путей в кружке указывается минимальное значение. Например, попасть в пункт можно из пунктов , и , но кратчайшее расстояние от этих пунктов к пункту будет из пункта - 31 км. Тогда как расстояние из пункта равно 39 км, а из пункта - 38 км. На сети дорог возле пункта изображены два кружка, в которых записаны значения кратчайших расстояний при движении по оптимальным траекториям. Оптимальная траектория при движении от пункта к пункту отмечена жирной стрелкой, а в обратном направлении – дополнительной стрелкой.

Анализ оптимальной траектории. В соответствии с оптимальной траекторией коммивояжер должен посещать пункты в следующей последовательности: , , , , , ,, , , , , . При этом ему придется проехать 222 км.

Для той же сети дорог определим кратчайшие расстояния из пункта во все остальные. Такая задача часто возникает при выполнении полевых топографо-геодезических работ, когда надо переехать с одного участка работ на другой. На первом этапе определяем кратчайшее расстояние между пунктами и , задачу решаем с конца, расстояние равно 84 км (рис. 2).

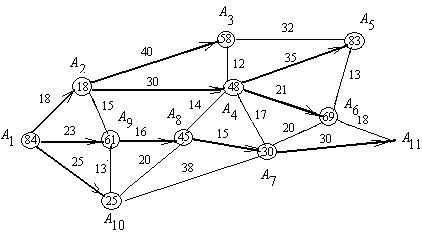
Рис.2. Кратчайшие пути от пункта до всех остальных пунктов

Расстояния во все остальные пункты, не лежащие на пути -, начинаем определять от пункта . Значения кратчайших расстояний записаны в кружках у соответствующих пунктов. Кратчайшие пути отмечены жирными стрелками.

В работе [6] задача о кратчайшем пути решалась на модели транспортной задачи.

Таким образом, методом динамического программирования можно довольно просто решать задачи выбора оптимальных схем транспортных перевозок, радиорелейных и телевизионных сетей, мелиорационных и ирригационных систем любой сложности.

Литература:

1. Брыкин П.А. Математическое программирование в планировании геодезических и топографических работ / П.А. Брыкин, С.А. Киммельман. – М.: Недра, 1972. – 232 с.

2. Грешилов А.А. Как принять наилучшее решение в реальных условиях / А.А. Грешилов. – М.: Радио и связь, 1991. – 320 с.

3. Ершова Н.М. Математические методы и модели: Конспект лекций / Н.М.Ершова. – Днепропетровск: ПГАСА, 2009. – *112 с.

4. Ершова Н.М. Экономико-математическое моделирование: Конспект лекций / Н.М. Ершова. – Днепропетровск: ПГАСА, 2008. – 248 с.

5. Кузнецов А.В. Высшая математика. Математическое программирование: Учебник для вузов / А.В. Кузнецов, В.А. Сакович, Н.И. Холод. – Минск: Вышэйшая школа, 1994. – 286 с.

6. Фролькис В.А. Введение в теорию и методы оптимизации для экономистов. 2-е изд. / В.А. Фролькис. – Спб: Питер, 2002. – 320 с.