Флорескул Надія Петрівна

аспірант кафедри фінансів

Київський національний торговельно-економічний університет

Кореляційно – регресійний аналіз в бюджетній системі України

Доходи та видатки бюджету, які утворюються і використовуються для реалізації програм соціально – економічного розвитку, зміцнення матеріально – фінансової бази, є бюджетом розвитку. Структура та розмір видатків бюджету впливають на досягнення цілей соціально-економічного розвитку.

Дослідимо особливості впливу структури та розміру видаткової частини державного бюджету на характеристики розвитку економіки України, використовуючи кореляційно-регресійний аналіз. Він дозволяє дослідити кореляційний зв’язок між ВВП держави та видатками за окремими статтями, побудувати рівняння регресії, що описує цей зв'язок, і визначити комплексний механізм впливу на зростання ВВП країни змін величини видатків за окремими статтями, а також виміряти тісноту, напрям зв’язку, тощо.

Для побудови багатофакторної лінійної економетричної моделі сумарного впливу зміни величини видатків визначимо перелік факторів, які мають найбільш вагомий вплив на динаміку економічного зростання:

-         видатки на державне управління ();

-         видатки на економічну діяльність ;

-         видатки ЖКГ ;

-         видатки на охорону здоров’я ;

-         видатки на духовний та фізичний розвиток ;

-         видатки на освіту ;

-         видатки на соціальний захист та соціальне забезпечення .

Показники видатків зазначених факторів наведемо у  Таблиці 1.

Таблиця 1.

Показники ВВП та видатків зведеного бюджету України у 1999-2007 р.р.

Рік

Валовий внутрішній продукт,

Видатки на державне управління, Х1

Видатки на економічну діяльність, Х2

Видатки на ЖКГ, Х3

На охорону здоров’я, Х4

На дух та фіз. розвиток, Х5

На освіту, Х6

Соціальний захист та соц. заб., Х7

1999

130442

49061,3

3613,9

20,2

49254,5

129,7

1448,7

2196,5

2000

170070

3384,8

6186,3

1084,1

531,4

838,7

6633,1

7586,1

2001

204190

4738,8

6727,5

1555,2

5461,2

1122,9

8880,8

10156,8

2002

225810

6872,3

7200,9

1407,6

7537,9

1417,9

12269

12643,9

2003

267344

7862,5

12215,5

1823,3

9708,2

2052,5

14977,7

12953,2

2004

345113

9654,8

18703,8

2665,3

12159,4

2695,9

18333,2

19310,5

2005

441452

11980,5

19115,1

3914,2

15476,5

3449,8

26801,8

39940,2

2006

544153

14165,2

27341,1

8024,1

19737,7

4328,4

33785

41419,9

2007

712945

16906,6

40523,4

5900,3

26717,6

5687,8

44333,6

48517,3

Джерело: Статистичний збірник за 2007 рік.

 

Теоретична модель лінійної множинної регресії, що описує кореляційно-регресійний зв’язок змінної  з  формалізується у наступному вигляді:

+                                      (1)

де  – невідомі теоретичні параметри регресії, а  – випадкове теоретичне відхилення. Якщо (*.1) переписати для кожного з n індивідуальних спостережень (в нашому випадку є 8 років), то матимемо наступну систему співвідношень

                       (2)

Основною задачею множинного регресійного аналізу є оцінка теоретичних параметрів регресії, тобто заміна системи (*.2) на систему

,                      (3)

де , , …,  – шукані оцінки теоретичних параметрів , а  – оцінка теоретич­но­го відхилення  .

Найбільш поширеним методом оцінки параметрів множинної лінійної регресії є метод найменших квадратів, зміст якого полягає в мінімізації суми квадратів відхилень спостережуваних значень залежної змінної  від значень, отриманих на основі побудованого рівняння регресії.

Для знаходження оцінок множинної лінійної регресії зручніше користуватись матрично-векторною формою відповідних співвідношень, що, безперечно, дозволяє записати їх у більш згорнутому і лаконічному вигляді. Тоді в матричній формі моделі (2) і (3) запишуться наступним чином:

,                                              (4)

,                                              (5)

де , , ,  ,  ,  .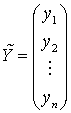

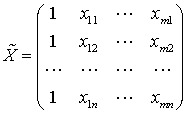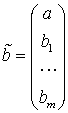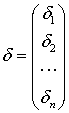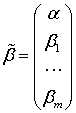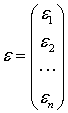Вектор-оцінка  знаходиться за формулою:

                                      (6)

Знайти вектор (6) можна по-різному, зокрема використовувати MS Excel, Statistica, Eviews тощо. У всіх вказаних програмах є вбудовані функції або модулі, які знаходять оцінки регресії.

Таким чином, використовуючи пакет аналізу в MS Excel Регресия дані Таблиці 1., побудована економетрична модель отримає вигляд:

+

+.

Коефіцієнт детермінації фактично дорівнює 1 і означає, що зміни величини реального ВВП пояснюються, в значній мірі, саме змінами у відібраних видах видатків.

Для сукупності величин  можна знайти кореляційну матрицю

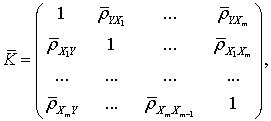                              ( 7 )

де .

Коефіцієнти кореляційної матриці використовується для вимірювання сили лінійних зв’язків різних пар змінних, при цьому враховується, що зв’язок кожної пари змінних знаходиться під впливом зв’язків із іншими змінними.

Матриця  є симетричною відносно головної діагоналі .

Кореляційна матриця має вигляд:

1

 

 

 

 

 

 

 

-0,099

1

 

 

 

 

 

 

0,989

-0,077

1

 

 

 

 

 

0,904

-0,151

0,871

1

 

 

 

 

0,141

0,969

0,162

0,058

1

 

 

 

0,994

-0,177

0,983

0,906

0,063

1

 

 

0,996

-0,165

0,978

0,911

0,076

0,997

1

 

0,969

-0,134

0,928

0,914

0,092

0,968

0,975

1

 

Видно, що між досліджуваними змінними існує дуже тісний лінійний зв’язок, крім пари ( і ) та ( і ), тобто =-0,099 і =-0,141.

Література: