Математика /4. Прикладная математика/

Рябоштан А. Ф., к.т.н. Миленин А.Н.

Харьковский национальный технический университет сельского хозяйства

имени П. Василенко

Конструирование линейного каркаса двумерного обвода лопатки газовой турбины

Аналитическое описание двумерных обводов при помощи интерполяционных формул не всегда оказывается удобным ввиду того, что не предполагает получение определенных линий на поверхности. Задачи получения линейного каркаса обвода лопатки газовой турбины является основной при конструировании зализов, различных переходных и стыковочных поверхностей при заполнении пространственного криволинейного четырехугольника (порции пространства).

Пусть заданы полосы II порядка

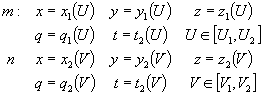
Остальные частные производные , полос рассчитываются по известным соотношениям:

,

, (3)

Задача заключается в построении каркаса отсека на ребрах и удовлетворяющего заданному оснащению. Очевидно, что она имеет не единственное решение, как в смысле применения, так и в неопределенности выбора «поперечных» касательных и вторых производных на ребрах обвода порции пространства (они будут первыми и вторыми производными линий каркаса).

Остановимся на следующей схеме конструирования. Для каждой из проекций и применим формулу плоского обвода второго порядка гладкости, например

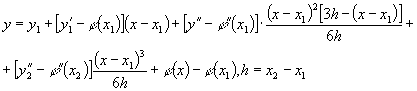(4)

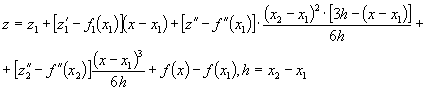(5)

Чтобы применить уравнение (4) и (5), необходимо, используя заданные , , , , на ребрах обвода порции межлопаточного пространства, каким то образом определить , , , . Этот выбор не является однозначным и осуществляется при помощи уравнений

, (6)

. (7)

Лучше всего задать значения (из множества допустимых) и на плоскости и по формулам определить и .

Допустим такой выбор сделан и функции , , , на ребрах определены.

Для заполнения всего отсека установим между и соответствие

(8)

Прежде чем рассчитывать обвод, желательно функции, задающие полосу , при помощи (8) выразить через (пусть это будут) , , … , . Тогда уравнения (4) и (5) будут иметь один параметр .

Функция двухпараметрическая

. (9)

Параметры и определяются из решения системы уравнений при , , , .

Таким образом, вводится функция для (5) и определяются ее параметры.

После определения функций и записываются уравнениями (4) и (5), совместное рассмотрение которых дает уравнение искомого отсека, состоящего из линии с .

При рассмотрении отсека, сопрягающего, две поверхности, на каждой из которых назначается линия сопряжения, и рассчитываются функции поперечных касательных и вторых производных вдоль линии сопряжения. Как правило, параметрические линии сопряжения и их производные можно назначить в виде , , , . Естественно, функции согласуются с функциями нормалей и кривизны поверхности вдоль линии сопряжения. При такой организации способа конструирования лопаток газовых турбин происходит сопряжение по второму порядку гладкости параметрических линий обеих поверхностей, что дает возможность организовывать сквозную параметризацию всей поверхности. Это оказывается удобным при решении целого комплекса инженерных задач.