Ph.D. M. E. Lustenkov, Ph.D. I. I. Makovetsky
Belorussian-Russian university, Mogilev, Republic of
Belarus
PLANAR PLANETARY TRANSMISSIONS WITH
ROLLING ELEMENTS
Abstract. The principles of the
development of the transmissions with intermediate rolling elements are
considered. These transmissions allow to create the speed reducers with small
axial dimensions. The algorithm of the transformation of the equations of the
cylindrical curves to the planar curves is given.
Keywords: planetary transmission,
rolling elements, reduction unit.
Planetary
transmissions with intermediate rolling elements have a number of advantages in
comparison with the well known planetary gears with teeth engagement. They have
an ability to reach the big reduction ratio in one stage, high overlap ratio, compactness.
The researchers in Belorussian-Russian university work on the development of
the reduction units which made on a base of the transmissions of the cylindrical
type [1] in which the centers of rolling elements move on the trajectories
lying on a cylindrical surface. Sometimes according to design requirements, however,
we have to build in the reduction unit in the constraint axial dimensions. In
this case the application of the planar transmission is preferred.
The
planetary transmission with intermediate rolling elements consists of three
main links. These links interact with each other by means of rolling elements.
Two of these links have closed periodical grooves and the third link has slots
or cuts. The form of closed periodical grooves is described by curve equations.
We need to define these equations for analytical investigation of the
transmission kinematics. The equations of curves for the transmissions of this
type are given in [2] including the equations of the sinusoids which lying on a
plane. The middle lines of these curves are closed in the circle, therefore,
these sinusoid are called as “circle-sinusoid” in [3].
We have
got the equations which differ from the results which are brought in [2]. The
equation of the planar sinusoid (circle-sinusoid) in polar system of
coordinates can be written as:
![]() (1)
(1)
where, R is the radius of the middle circle (the
changing of the radial coordinate ρ occurs relatively this middle circle),
A is the amplitude of sinusoid, φ is the polar angle, Zi is the number of
periods of sinusoids and i is the index
(number) of the link with the periodical grooves.
On the basis
of the equation (1) we have got the equations of the sinusoids in parametrical
form:


![]() (2)
(2)
where, t is a parameter which is performing the
function of an angular position and alternating from 0 to 2πR.
On basis
of the system of the equations (2) the curves have been drawn. They are shown on
figure 1: 1 is the single-period planar sinusoid, 2 is the middle circle,
3 is the many-period sinusoid. The parameters of interacting curves are: À=4 mm, R=20 mm, Z1=1, Z3=8.
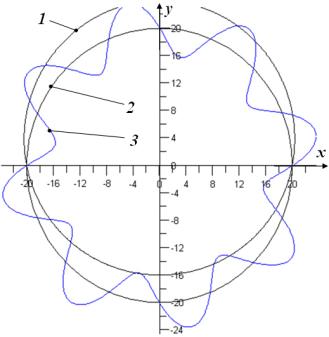
Fig. 1. The interaction of two planar sinusoids
The
practical realization of these equations is shown on figure 2. The transmission
[4, 5] consists of three disks (1, 2 and 3). The face surfaces of the disks 1 and
3 have the closed periodical grooves. The
disk 1 has a single-period and the disk 3 has a many-period grooves. The
intermediate disk 2 has the radial cuts in which the rolling elements (balls)
are moving. One of the main links (1, 2 or 3) is established as driving shaft, the second – as a driven shaft
and the rest link is a
stopped (connected with the housing) link. The transmission could work as a reduction unit, as a step-up gear and as a differential (without a stopped
link).

Fig. 2. The scheme of the planar planetary ball
transmission
One can
use not only sinusoids in the planar planetary transmissions with the rolling
elements. The system of the equations (2) could be brought to the general form (provided zi=0):

 (3)
(3)
where, f(A, R,
Zi) is the function which depends on the curve parameters and the
parameter t.
The
function f defines the equation of the unfolding of the
curve on the plane in Cartesian coordinate system. E. g. the equations of the system
of sectionally-screw curves (the set of alternating ascending and descending
straight line segments) lying on the plane can be written as:

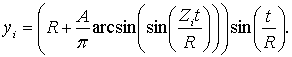 (4)
(4)
Thereby
we can design the transmission not only with the sinusoidal profile of periodical
grooves, but also with cycloid, circle and others profiles. But first we need to
analyze the advantages of one or another profile by means of the unfolding
equation of the given curve. The advantage of the curves on the equations (4) is
a constancy of their slopes. This raises the uniformity of the wear of the
grooves and stability of the reduction ratio.
References
1. M.E. Lustenkov, D.M. Makarevich, The planetary
ball transmissions of a cylindrical type: monograph, Mogilev, Belorussian-Russian
university, 2005, 123 p.
2. M.F.
Pashkevitch, V.V. Gerastschenko, Planetary ball and roller reduction gears and
their testings, Minsk, BelNIINTI, 1992, 248 p.
3. R.M.
Ignatistschev, Sinus-ball reduction gears, Minsk, Higher school, 1983, 107 p.
4. Ball planetary transmission: inventors certificate SU 1019148, USSR,
Int.cl. F16 Í13/08 / R.Ì. Ignatistschev. - ¹3399190/25-28; fill. 18.02.82; publ. 30.04.88// Discoveries.
Inventions, 1988, Bull.¹16.
5. Pat.
US 5312306, Speed converter, F16 H13/08 Cl.475-196, 476/36 / / F.A. Folino.
- Ser. N. 670263; fil. 04.03.1991; pat. 17.05.1994.