Технические науки / 3. Отраслевое машиностроение

К. т. н. Крупко В.Г., к.т.н. Паламарчук В.О., Стець О.М.

Донбаська державна машинобудівна академія, Краматорськ, Україна

Математичне моделювання термінів служби передатних механізмів екскаваторів-драглайнів

Для України одним із пріоритетних напрямків розвитку господарчого комплексу є видобуток корисних копалин відкритим способом, де основними складовими схем комплексної механізації гірничих робіт є екскаватори-драглайни виробництва ЗАТ НКМЗ.

Сучасні технологічні процеси по екскавації ґрунту з кар'єрів відкритим способом вимагають більшої віддачі від екскаваторів, у тому числі й від екскаваторів-драглайнів, підвищення їх продуктивності і надійності. Великі кошти витрачають для того, щоб машинний парк перебував у працездатному стані. На проведення планових ремонтів іде від 8 до 15% календарного часу, а непланових – від 3 до 7% [1]. Основними шляхами скорочення трудових і матеріальних витрат на проведення ремонтів екскаваторів є підвищення безвідмовності екскаваторів; збільшення строків служби деталей та вузлів екскаваторів, підвищення ремонтоздатності і ремонтної технологічності конструкцій екскаваторів, покращення організації і технічного рівня ремонтів.

Причиною більшості відмов крокуючих екскаваторів є порівняно невелика група деталей, ресурс яких обмежується їх інтенсивним зносом. До таких деталей належать зубчаті колеса. Більшість механізмів екскаваторів містять( до 60%) вузли із зубчатими передачами. Одним із важливіших параметрів, які характеризують екскаватор на стадії розробок та представлення безпосереднім замовникам є показники надійності. Були поставлені і розв’язані наступні задачі:

- зібрати статистичні дані про терміни служби і відмовам виконавчих механізмів екскаваторів-драглайнів;

- на основі обробки статистичних даних скласти математичну модель процесу визначення термінів служби;

- провести аналіз і отримати залежність термінів служби від модуля, числа зубів, твердості матеріалу, величини граничного зносу;

- дати оцінку адекватності моделі.

На кафедрі ПТМ Донбаської державної машинобудівної академії на протязі тривалого часу професором Кохом П. І. проводився збір статистичних даних по термінам служби екскаваторів. В таблиці 1 приведені результати досліджень П.І. Коха та дані ЗАТ НКМЗ.

В самому загальному випадку досліджуваний процес можна описати наступним рівнянням:

, (1)

де – відповідно модуль, число зубів, твердість матеріалу, величина граничного зносу; Т – середній строк служби в годинах

Таблиця 1

Зведені дані до розрахунку строків служби зубчастих коліс екскаваторів ЕШ 10/70А

№	Модуль, m	Число зубів, z	Твердість НВ	Величина граничного зносу, мм	Середній строк служби в год
1	10	190	210	1,73	15720
2	20	24	270	1,91	5360
3	20	114	210	2,25	18750
4	10	190	210	1,73	21520
5	20	24	270	1,91	11230
6	20	114	210	2,25	20450
7	8	30	260	1,67	27830
8	8	105	210	1,94	16160
9	12	24	280	2,66	38000
10	12	99	220	2,29	24250
11	16	90	220	2,15	18690
12	36	192	230	5,2	33330
13	8	126	210	1,67	19640
14	12	28	270	2,07	47040
15	12	112	210	2,495	29700
16	28	18	270	4,52	43880
17	28	53	210	3,64	33090
18	33	12	250	3,12	62400
19	33	69	245	3,54	51300

Аналіз рівняння (1) дозволив отримати критеріальне рівняння

(2)

В якості досліджуваної математичної моделі прийнята функція

(3)

Оцінювання даної функціональної залежності відбувається методом системи STATISTIKA в середовищі Windows [2].

Розрахункові значення коефіцієнтів приведені в таблиці 2.

Таблиця 2

Коефіцієнти входу в критеріальну залежність

	а0	а1	а2	а3	а4
Estimate	21,29425	-0,012070	-0,085689	1,265215	0,704482

Оцінку адекватності моделі здійснювали непрямим методом, шляхом аналізу залишків, тобто різниці між істинними значеннями параметру Т і передбаченими математичною моделлю. У випадку, коли модель адекватна, залишки мають нормальний розподіл /2/. На рисунку 1 приведена гістограма залишків

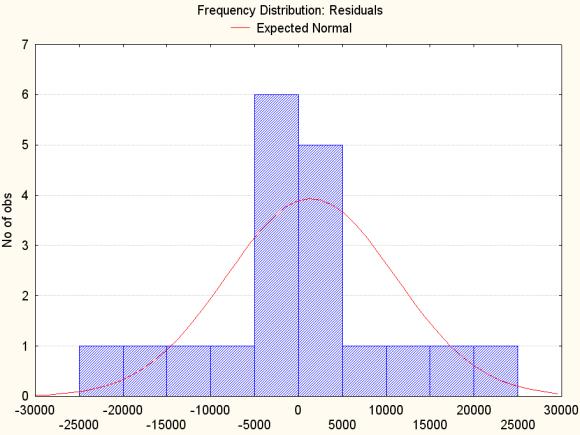
Рисунок 1 – Гістограма залишків з накладанням щільності нормального розподілу.

Розрахунки по критерію Пірсона [3] підтвердили гіпотезу про їх нормальний розподіл.

Таким чином, розроблена математична модель дозволяє прогнозувати значення строків служби деталей передатних механізмів екскаваторів-драглайнів, а в наслідок цього і прогнозувати норми запасних частин для капітальних і середніх ремонтів.

Література:

1. Кох П.И. Ремонт экскаваторов. / Кох П.И. – М.:Изд-во "Недра", 1979.

2. Боровиков В.П. Статистический анализ и обработка данных в среде Windows./ Боровиков В.П., Боровиков И.П. – М.:Филинь,1998. – 608 с.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. / М.: Высшая школа,1972. – 368 с.