Технические науки/2. Механика
Адлуцкий В.Я.
Днепропетровский национальный университет, Украина
ЧИСЛЕННЫЙ
АНАЛИЗ ПРОЦЕССА РАЗРУШЕНИЯ
В ТОНКИХ ПЛАСТИНАХ
В работе [1]
предложен алгоритм численного моделирования процесса распространения трещин в
тонких пластинах на основе МКЭ с использованием энергетического критерия
разрушения. В настоящей работе приводится ряд примеров реализации указанного алгоритма.
 Пример 1. Рассматривается
пластина с размерами в плане
Пример 1. Рассматривается
пластина с размерами в плане ![]() и толщиной h. Задано следующее соотношение геометрических параметров:
и толщиной h. Задано следующее соотношение геометрических параметров: ![]()
![]() . Значение коэффициента Пуассона
. Значение коэффициента Пуассона ![]() =0,3. Пластина жестко защемлена вдоль стороны x=0 и нагружена двумя противоположно направленными силами
величиной Р каждая, приложенными в
точках с координатами
=0,3. Пластина жестко защемлена вдоль стороны x=0 и нагружена двумя противоположно направленными силами
величиной Р каждая, приложенными в
точках с координатами ![]() в направлении оси у (рис.1).
в направлении оси у (рис.1).
Исходная трещина
длиной ![]() расположена на прямой
расположена на прямой
![]() , ее левый конец примыкает к зоне защемления. В силу
симметрии рост трещины происходит вдоль прямой
, ее левый конец примыкает к зоне защемления. В силу
симметрии рост трещины происходит вдоль прямой ![]() . На рис. 1 приведены
графики критических нагрузок для двух случаев приложения сил:
. На рис. 1 приведены
графики критических нагрузок для двух случаев приложения сил: ![]() – кривая 1,
– кривая 1, ![]() – кривая 2. Кривая 3
соответствует точному решению для бесконечной пластины при
– кривая 2. Кривая 3
соответствует точному решению для бесконечной пластины при ![]() [2]. Как следует из
приведенных данных, при
[2]. Как следует из
приведенных данных, при ![]() решения для пластины
конечных размеров при различных значениях d практически совпадают. При этом в интервале
решения для пластины
конечных размеров при различных значениях d практически совпадают. При этом в интервале ![]() процесс разрушения
носит локально устойчивый характер. В случае
процесс разрушения
носит локально устойчивый характер. В случае ![]() решения для конечной
и бесконечной пластин при
решения для конечной
и бесконечной пластин при ![]() достаточно близки. На
конечном этапе разрушения имеет место некоторое повышение уровня критических
нагрузок вследствие развития изгибных деформаций перед фронтом трещины и
создания зоны сжатия, затрудняющей ее рост.
достаточно близки. На
конечном этапе разрушения имеет место некоторое повышение уровня критических
нагрузок вследствие развития изгибных деформаций перед фронтом трещины и
создания зоны сжатия, затрудняющей ее рост.
Представляет
интерес исследование влияния несимметричности граничных условий и нагрузок, а
также нарушений сплошности материала на характер распространения трещин.
 Пример 2. Рассматривается
пластина с геометрическими и физическими параметрами из предыдущего примера,
жестко защемленная вдоль краев
Пример 2. Рассматривается
пластина с геометрическими и физическими параметрами из предыдущего примера,
жестко защемленная вдоль краев ![]() и
и ![]() и нагруженная
равномерно распределенной нагрузкой интенсивности р вдоль края
и нагруженная
равномерно распределенной нагрузкой интенсивности р вдоль края ![]() . Пластина ослаблена исходной трещиной длиной
. Пластина ослаблена исходной трещиной длиной ![]() , расположенной на прямой
, расположенной на прямой ![]() , с левым концом, примыкающим к зоне защемления.
, с левым концом, примыкающим к зоне защемления.
 На рис.2 сплошной линией
изображен график зависимости критической нагрузки от номера шага подрастания
трещины Процесс роста трещины неустойчив. Траектория распространения трещины
является криволинейной, при этом рост трещины на начальных шагах подрастания
происходит в сторону защемленного горизонтального края, затем
– параллельно ему, и на конечной стадии трещина несколько смещается в
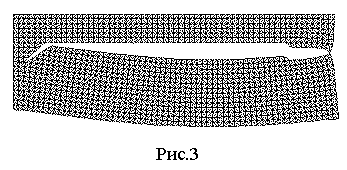
сторону загруженного края. На рис 3 представлено деформированное состояние
пластины с трещиной непосредственно перед завершением процесса разрушения.
На рис.2 сплошной линией
изображен график зависимости критической нагрузки от номера шага подрастания
трещины Процесс роста трещины неустойчив. Траектория распространения трещины
является криволинейной, при этом рост трещины на начальных шагах подрастания
происходит в сторону защемленного горизонтального края, затем
– параллельно ему, и на конечной стадии трещина несколько смещается в
сторону загруженного края. На рис 3 представлено деформированное состояние
пластины с трещиной непосредственно перед завершением процесса разрушения.
Та
же задача рассматривалась при наличии в пластине двух отверстий, одно из которых
расположено достаточно далеко от траектории роста трещины, а второе – вблизи
нее. Значения критической нагрузки для этого случая приведены на рис.2 точками.
Как видно из графика, влияние первого отверстия на величину критической
нагрузки минимально. Оно создает эффект "затенения", вызывая слабый
рост критической нагрузки при прохождении трещиной зоны его влияния. Наличие первого отверстия также не оказывает
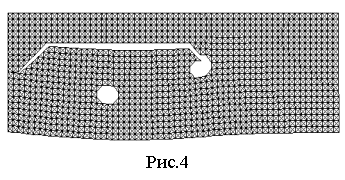
никакого воздействия на направление развития трещины. Роль второго отверстия
качественно иная: оно играет роль "ловушки", изменяя траекторию
трещины и, в конечном итоге, прервая ее
распространение (рис.4).
До сих пор
рассматривался процесс распространения трещин
под влиянием нагрузок,
действующих в плоскости пластины, т.е. в условиях обобщенного плоского
напряженного состояния. Представляет
интерес изучение особенностей распространения трещин при изгибе пластины под
действием нагрузок, нормальных к срединной поверхности. При этом, в отличие от
первого (отрывного) типа разрушения, в данном случае реализуется процесс
разрушения третьего типа (резание),
когда одна поверхность трещины скользит по другой параллельно фронту
трещины и деформация является кососимметричной относительно срединной
поверхности. В используемом критерии разрушения ![]() критическое значение J-интеграла
критическое значение J-интеграла ![]() отлично от
отлично от ![]() и так же, как и
и так же, как и ![]() , подлежит экспериментальному определению.
, подлежит экспериментальному определению.
 Пример 3. Пластина с теми же параметрами, что и в
предыдущем примере. жестко защемлена вдоль края
Пример 3. Пластина с теми же параметрами, что и в
предыдущем примере. жестко защемлена вдоль края ![]() и ослаблена исходной
трещиной длиной
и ослаблена исходной
трещиной длиной ![]() , расположенной симметрично относительно оси х в центральном сечении
, расположенной симметрично относительно оси х в центральном сечении ![]() . В центре трещины на обоих берегах нормально к срединной
поверхности пластины приложены две противоположно направленные силы величиной Р каждая.
. В центре трещины на обоих берегах нормально к срединной
поверхности пластины приложены две противоположно направленные силы величиной Р каждая.
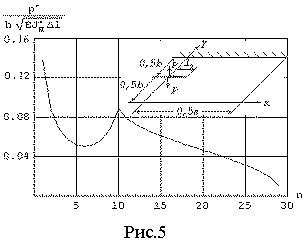
На рис.5 представлен график зависимости критической нагрузки от номера
шага подрастания трещины ![]() , а на рис.6 – деформированное состояние симметричной части
пластины непосредственно перед полным разрушением с образованием двух
фрагментов. Как следует из приведенных данных, процесс разрушения начинается
путем образования двух симметричных относительно оси у трещин, исходящих из вершин исходной трещины под углом
, а на рис.6 – деформированное состояние симметричной части
пластины непосредственно перед полным разрушением с образованием двух
фрагментов. Как следует из приведенных данных, процесс разрушения начинается
путем образования двух симметричных относительно оси у трещин, исходящих из вершин исходной трещины под углом ![]() по направлению к
защемленному краю. По мере приближения к этому краю процесс распространения трещины
становится устойчивым. При достижении окрестности защемленного края трещины
поворачивают, и дальнейший их рост происходит параллельно краю и носит неустойчивый характер.
по направлению к
защемленному краю. По мере приближения к этому краю процесс распространения трещины
становится устойчивым. При достижении окрестности защемленного края трещины
поворачивают, и дальнейший их рост происходит параллельно краю и носит неустойчивый характер.

Пример
4. Рассматривается изгиб пластины с геометрическими параметрами ![]() . Пластина жестко
защемлена по всему контуру и нагружена равномерно распределенной нормальной
нагрузкой интенсивности q. В
центре пластины расположена исходная трещина длиной
. Пластина жестко
защемлена по всему контуру и нагружена равномерно распределенной нормальной
нагрузкой интенсивности q. В
центре пластины расположена исходная трещина длиной ![]() .
.

На рис.7
изображены графики зависимости критической нагрузки от номера шага подрастания
трещины ![]() для двух вариантов
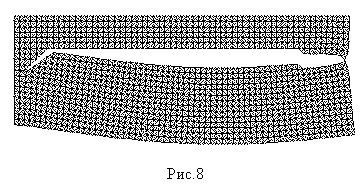
длины исходной трещины. На рис.8 приведены
деформированные состояния четверти пластины для этих вариантов непосредственно
перед полным разрушением.
для двух вариантов
длины исходной трещины. На рис.8 приведены
деформированные состояния четверти пластины для этих вариантов непосредственно
перед полным разрушением.

Как следует из
приведенных данных, длина исходной трещины оказывает существенное влияние на
вид разрушения. В случае короткой исходной трещины (![]() ) (рис.8,а)
разрушение начинается путем образования четырех симметричных трещин, исходящих
из вершин исходной трещины. Первоначально удаляясь от оси х, они затем поворачивают и сближаются, формируя два фрагмента
лепесткообразной формы перед фронтом исходной трещины. В итоге пластина
разделяется на три фрагмента. В случае более длинной исходной трещины (
) (рис.8,а)
разрушение начинается путем образования четырех симметричных трещин, исходящих
из вершин исходной трещины. Первоначально удаляясь от оси х, они затем поворачивают и сближаются, формируя два фрагмента
лепесткообразной формы перед фронтом исходной трещины. В итоге пластина
разделяется на три фрагмента. В случае более длинной исходной трещины (![]() ) (рис.8,б) также происходит разделение пластины на три фрагмента,
но при этом два формирующихся фрагмента примыкают к берегам исходной
трещины.
) (рис.8,б) также происходит разделение пластины на три фрагмента,
но при этом два формирующихся фрагмента примыкают к берегам исходной
трещины.
Реализованный в
данной работе алгоритм численного моделирования процесса распространения трещин
в тонких пластинах позволяет эффективно решать достаточно сложные задачи
линейной теории разрушения. Как следует из приведенных результатов, характер
протекания процесса разрушения и его конечный результат существенно зависят от
таких факторов, как геометрические размеры пластины, вид граничных условий, тип
нагрузки, размеры и расположение исходной трещины, наличие других несовершенств
и т.д.
Литература:
1.
Ободан
Н.И., Адлуцкий В.Я. Конечноэлементное моделирование процесса распространения
трещин в тонких пластинах. – В настоящ. изд.
2.
Партон
В.З. Морозов Е.М. Механика упругопластического разрушения: Основы механики
разрушения . – М., 2008. – 352 с.
3.
Партон
В.З. Морозов Е.М. Механика упругопластического разрушения: Специальные задачи
механики разрушения . – М., 2008. – 192 с.