Технические науки/2. Механика
Громов В. А.
Днепропетровский
национальный университет им. О. Гончара, Украина
Метод
наилучшего базиса в
нелинейных
краевых задачах теории пологих оболочек
Неослабевающий интерес к анализу решений нелинейных краевых задач теории пологих оболочек обусловлен широким практическим применением тонкостенных оболочечных конструкций в различных областях современной техники и сложностью численного построения указанных решений и анализа картины закритического ветвления.
Рассматриваются
уравнения теории пологих оболочек, которые для случая цилиндрической оболочки
принимают вид:
 ,
,
 . (1)
. (1)
Здесь и далее: ![]() ,
, ![]() ,
, ![]() – длина, радиус и
толщина оболочки соответственно;
– длина, радиус и
толщина оболочки соответственно; ![]() , где
, где ![]() – коэффициент Пуассона
материала оболочки;
– коэффициент Пуассона
материала оболочки; ![]() ,
, ![]() ,
, ![]() ,
, ![]() –
безразмерные продольная и окружная координаты (чертой сверху помечены размерные
величины);
–
безразмерные продольная и окружная координаты (чертой сверху помечены размерные
величины); ![]() ,
, ![]() – безразмерные
нормальный прогиб и функция усилий;
– безразмерные
нормальный прогиб и функция усилий; ![]() – функция внешнего
давления, действующего на оболочку, представлена в виде произведения функций
одной переменной; оператор
– функция внешнего
давления, действующего на оболочку, представлена в виде произведения функций
одной переменной; оператор ![]() даётся выражением:
даётся выражением:
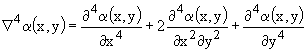 . (2)
. (2)
На границах ![]() формулируются краевые
условия, которые вместе с уравнениями (1) и требованием замкнутости (
формулируются краевые
условия, которые вместе с уравнениями (1) и требованием замкнутости (![]() -периодичности) решения в окружном направлении образуют
нелинейную краевую задачу для определения напряжённо-деформированного состояния
нагруженной цилиндрической оболочки.
-периодичности) решения в окружном направлении образуют
нелинейную краевую задачу для определения напряжённо-деформированного состояния
нагруженной цилиндрической оболочки.
В общем виде соотношения (1) могут быть
представлены в виде
![]()
![]() ,
(3)
,
(3)
где ![]() - оператор обратный
оператору
- оператор обратный
оператору ![]() , определённому соотношением (2); нелинейные операторы
, определённому соотношением (2); нелинейные операторы ![]() ,
, ![]() действуют в
пространствах
действуют в
пространствах ![]() , введённых для анализа нелинейных краевых задач теории
пологих оболочек И. И. Воровичем. В этой же работе доказано существование
решений нелинейной краевой задачи (1) – функций
, введённых для анализа нелинейных краевых задач теории
пологих оболочек И. И. Воровичем. В этой же работе доказано существование
решений нелинейной краевой задачи (1) – функций ![]() ,
, ![]() .
.
Зададимся целью отыскать функции ![]() ,
, ![]() ,
, ![]() ,
, ![]() и величины
и величины ![]() и
и ![]() наилучшим образом
приближающие неизвестные функции
наилучшим образом
приближающие неизвестные функции ![]() ,
, ![]() :
:
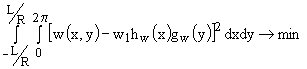 (4.1)
(4.1)  . (4.2)
. (4.2)
Функции ![]() ,
, ![]() в выражениях (4) не
вариируются – это вполне определённые (хотя и неизвестные нам) функции –
неизвестными являются и подлежат вариации функции
в выражениях (4) не
вариируются – это вполне определённые (хотя и неизвестные нам) функции –
неизвестными являются и подлежат вариации функции ![]() ,
, ![]() ,
, ![]() ,
, ![]() и величины
и величины ![]() и
и ![]() . В дальнейшем изложении ограничимся преобразованиями (4.1) –
преобразования для (4.2) осуществляются аналогично.
. В дальнейшем изложении ограничимся преобразованиями (4.1) –
преобразования для (4.2) осуществляются аналогично.
Вариация данного соотношения по ![]() с учётом соотношений
(3) даёт уравнение
с учётом соотношений
(3) даёт уравнение
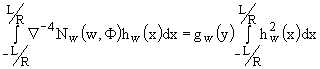 .
(5)
.
(5)
Четырёхкратное дифференцирование по ![]() выражения (4) даст
соотношение
выражения (4) даст
соотношение
 ;
(6)
;
(6)
двукратное дифференцирование по ![]() выражения (4) с
последующим двукратным применением формулы интегрирования по частям –
выражения (4) с
последующим двукратным применением формулы интегрирования по частям –
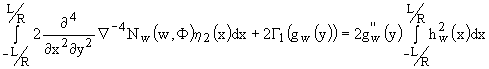 ; (7)
; (7)
четырёхкратное применением формулы интегрирования по
частям –
 . (8)
. (8)
Здесь ![]() -
- ![]() -кратный интеграл от
-кратный интеграл от ![]() ;
; ![]() ,
, ![]() - выражения,
выходящие на границы промежутка интегрирования при применении процедуры
интегрирования по частям. Заменяя
- выражения,
выходящие на границы промежутка интегрирования при применении процедуры
интегрирования по частям. Заменяя ![]() на
на ![]() , где
, где ![]() определяются из
условий минимума выражений
определяются из
условий минимума выражений
 ,
, ![]() , (9)
, (9)
суммируя таким образом преобразованные соотношения
(5)-(8) и подставляя вместо ![]()
![]() , в пренебрежении
, в пренебрежении ![]() получаем систему
интегро-дифференциальных уравнений относительно
получаем систему
интегро-дифференциальных уравнений относительно ![]() ,
, ![]() . В сочетании с граничными условиями, аналогичными
соотношениями, получаемыми при вариации (4.1) по
. В сочетании с граничными условиями, аналогичными
соотношениями, получаемыми при вариации (4.1) по ![]() и вариации (4.2) по
и вариации (4.2) по ![]() ,
, ![]() , условиями
стационарности (4.1), (4.2) по
, условиями
стационарности (4.1), (4.2) по ![]() и
и ![]() получаем замкнутый
набор уравнений для отыскания
получаем замкнутый
набор уравнений для отыскания ![]() ,
, ![]() ,
, ![]() ,
, ![]() и величины
и величины ![]() и
и ![]() . Для уточнения полученных решений формируются разрешающие
соотношения на основе функционала вида:
. Для уточнения полученных решений формируются разрешающие
соотношения на основе функционала вида:
 (10)
(10)