Технические науки/2. Механика

Ободан Н.И., Адлуцкий В.Я.

Днепропетровский национальный университет, Украина

КОНЕЧНОЭЛЕМЕНТНОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА

РАСПРОСТРАНЕНИЯ ТРЕЩИН В ТОНКИХ ПЛАСТИНАХ

Для получения достаточно адекватных результатов при моделировании процессов разрушения во многих случаях используется линейная теория Гриффитса [2,4,5]. В качестве критерия разрушения в настоящее время наибольшее распространение получил энергетический критерий, основанный на концепции инвариантного J-интеграла Черепанова-Райса [1,2,4,5].

Рассматривается тонкая пластина с размерами в плане и толщиной h, из материала с упругими константами Е и , где Е – модуль Юнга, – коэффициент Пуассона. Пластина содержит исходное повреждение в виде трещины, размеры которой малы в сравнении с размерами пластины. Деформация пластины осуществляется под действием нагрузок, способных вызвать дальнейшее распространение трещины. Ставится задача определения критических нагрузок, при которых происходит рост трещины, характера устойчивости этого процесса, а также нахождения траектории трещины вплоть до момента возможного разделения пластины на фрагменты.

Моделирование процесса распространения трещины осуществляется с помощью МКЭ. Для дискретизации пластины используется конечноэлементная сетка, состоящая из трехузловых изопараметрических треугольных элементов, позволяющих учитывать как мембранные, так и изгибные факторы. В качестве критерия разрушения выбирается локальный энергетический критерий на основе инвариантного J-интеграла Черепанова-Райса. Считается, что трещина начинает распространяться при условии , где – предельное значение J-интеграла.

Для решения вопроса о направлении дальнейшего распространения трещины, на каждом шаге процесса нагружения выбирается веер возможных направлений роста, исходя из топологии конечноэлементной сетки в окрестности текущей вершины трещины. После вычисления J-интеграла для каждого из таких направлений, за истинное направление распространения трещины выбирается то, которому соответствует экстремальное значение J-интеграла.

Критерий разрушения дает возможность определить значение критической нагрузки, при которой происходит старт трещины. Если значение нагрузки в расчете равно Р и максимальное значение J-интеграла при этом достигает значения J, то вследствие линейности используемой модели разрушения следует, что 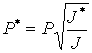, где – значение критической нагрузки.

Пусть текущая вершина трещины находится в узле М конечноэлементной сетки. Множество элементов конечноэлементной сетки, примыкающих к вершине М , обозначим через , , где N – общее число конечных элементов. Через и обозначим ближайшие к вершине М узлы на берегах трещины, остальные узлы обозначим через , . Введем локальную ортогональную декартову систему координат с началом в точке М, направив ось вдоль отрезка (рис.1,а). Любой отрезок , определяет одно из потенциально возможных направлений роста трещины. Направлению во введенной системе координат ставится в соответствие полярный угол . Предположение о росте трещины в направлении приводит к необходимости моделирования разреза вдоль отрезка , что, в свою очередь, связано с разбиением множества на два – и : , где – полярный угол, соответствующий внутренней точке элемента , например – его центру.

На рис 1,б множество заштриховано. Для моделирования участка трещины, образовавшегося вдоль отрезка все элементы множества переопределяются таким образом, что узел М в них заменяется вновь введенным узлом , геометрически совпадающим с М, но не тождественным ему. Для элементов множества узел М остается неизменным, и ему придается смысл узла . Таким образом осуществляется разрыв связей между элементами множеств и в узле М. Новая вершина М перемещается в узел .

Приведенные ниже результаты получены с использованием регулярной сетки КЭ, состоящей из квадратных ячеек размером , каждая из которых разбита диагоналями на четыре прямоугольных треугольника. Выбор такой сетки, помимо простоты генерации, удобен для моделирования роста трещины из данной вершины в семи возможных направлениях (не считая направления уже существующего разреза). Предусмотрена возможность выхода трещин на границу исследуемой области, в том числе, на границы отверстий и уже имеющихся трещин, вследствие чего изменяется связность области.

Пример 1. Рассматривается пластина с размерами в плане и толщиной h, растягиваемая вдоль краев и равномерно распределенной нагрузкой интенсивности p, содержащая в центральном сечении трещину длиной , левый конец которой расположен в центре пластины (рис.2).

Задано следующее соотношение геометрических параметров: . Значение коэффициента Пуассона =0,3. Вследствие эксцентриситета расположения начальной трещины максимальное значение J-интеграла в правой вершине трещины превышает значение в левой, и рост трещины происходит вправо. В силу симметрии развитие трещины осуществляется вдоль прямой . На рис.2 приведен график зависимости критической нагрузки от длины трещины (кривая 1). Здесь же приведено точное решение [4] для бесконечной пластины, растягиваемой равномерно распределенной на бесконечности нагрузкой параллельно оси (кривая 2): , где – критическое значение J-интеграла для трещин отрывного типа.

Как следует из сравнения результатов, для малых значений длин трещин решения обеих задач близки, а далее с ростом трещины критическая нагрузка для пластины конечных размеров убывает значительно быстрее, чем для бесконечной пластины, что связано с меньшей жесткостью первой. Поскольку во всем диапазоне длин l, то процесс распространения трещины носит неустойчивый характер.

Пример 2. Рассматривается пластина с размерами в плане и толщиной h, содержащая в центральном сечении начальную трещину с полудлиной . Пластина нагружена двумя противоположно направленными силами величиной Р каждая, приложенными в точках с координатами в направлении оси у (рис.4). В силу симметрии развитие трещины осуществляется вдоль прямой в обе стороны.

На рис.4 приведены графики зависимостей критической нагрузки от длины трещины ( – кривая 1, – кривая 2). Здесь же приведены точные решения [4] для бесконечной пластины с трещиной при тех же нагрузках ( – кривая 3, – кривая 4):

, .

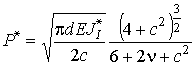Как следует из приведенных данных, решения для пластины конечных размеров при различных значениях d практически совпадают при , при этом процесс разрушения носит неустойчивый характер. Для при малых длинах трещины решения для конечной и бесконечной пластин близки, но с ростом трещины наблюдаются качественные различия в характере поведения критических нагрузок: для бесконечной пластины они соответствуют устойчивому процессу разрушения, а для конечной, как уже отмечено, – неустойчивому. Для результаты для конечной и бесконечной пластин существенно разнятся во всем диапазоне изменения длин трещины. Указанные различия связаны с меньшей жесткостью конечной пластины в сравнении с бесконечной.

Реализованный в данной работе алгоритм численного моделирования процесса распространения трещин в тонких пластинах позволяет эффективно решать достаточно сложные задачи линейной теории разрушения. Предложенный алгоритм может быть использован также для анализа процесса разрушения более сложных тонкостенных конструкций, например, оболочечных.

Литература:

1. Качанов Л.М. Основы механики разрушения. – М., 1974. – 312 с.

2. Керштейн И.М. Клюшников В.Д., Ломакин Е.В. Основы экспериментальной механики разрушения/ – М., 1989. – 140 с.

3. Морозов Е.М. Никишков Г.П. Метод конечных элементов в механике разрушения . – М., 2008. – 256 с.

4. Партон В.З. Морозов Е.М. Механика упругопластического разрушения: Основы механики разрушения . – М., 2008. – 352 с.

5. Партон В.З. Морозов Е.М. Механика упругопластического разрушения: Специальные задачи механики разрушения . – М., 2008. – 192 с.