Мельник В.Н., Карачун В.В.

Национальный технический университет Украины «КПИ»

РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ В ГРАНИЧНЫХ УСЛОВИЯХ ЛИНИИ МЕРИДИАНА ПОПЛАВКОВОГО ПОДВЕСА ГИРОСКОПА

Поскольку рассматриваются замкнутые оболочки вращения, то в окружном направлении (вдоль параллели) следует ожидать периодичности силовых, кинематических полей, то есть они должны определенным образом зависеть от периодических функций типа cos kφ, sin kφ (k=0,1,…). В свою очередь, внешнее динамическое нагружение по трем направлениям может быть и непериодическим по координате φ. Но нагрузки

всегда можно, во всяком случае формально, представить в виде рядов Фурье по координате φ.

Поэтому считаем, что

Отыскиваемые функции ищем в виде:

Для дальнейшего удобства выпишем граничные условия вместе:

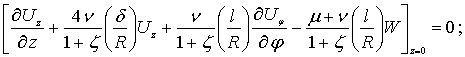(1)

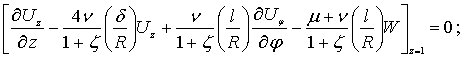(2)

Край . Выполним операцию разделения переменных в граничных условиях вида (1). С этой целью используем соотношения:

Тогда получим:

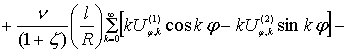
Сгруппируем слагаемые с :

(3)

сгруппируем слагаемые, содержащие :

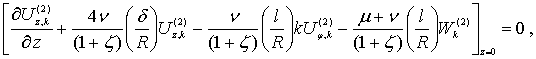
(3)

Край z=1. Проводим операцию разделения переменных в граничных условиях (2):

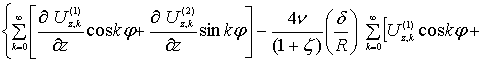
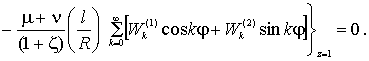
Сгруппируем слагаемые, содержащие :

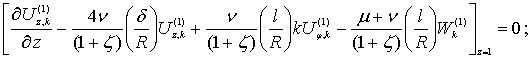(5)

сгруппируем слагаемые с :

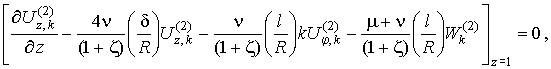
(6)

Проведенные аналитические исследования поплавкового подвеса гироскопа выполнены для самого общего случая функционирования прибора – поверхность оболочечной части предполагается нагруженной внешним возмущающим воздействием произвольной структуры и природы проявления, механизм воздействия на подвес может носить пространственный характер, либо выступать в качестве сосредоточенной на элементе поверхности нагрузки заданной интенсивности – и, поэтому, существенно расширяют возможности анализа динамики конструкции.

Результаты изучения расчетной модели могут быть сформулированы следующим образом:

- периодичность силовых и кинематических полей создает теоретическую базу для использования метода Фурье с целью приведения дифференциальных уравнений подвеса гироскопа к виду, удобному для интегрирования. Практически реализуется возможность независимого изучения динамического состояния поплавка по виду упругой деформации поверхности – осесимметричной (k=0), антисимметричной (k=1), циклического динамического деформирования (k ≥ 2).

- созданы предпосылки для выбора аналитических аппроксимаций упругих перемещений поплавка по трем направлениям и выбора корректирующих функций Кравчука для удовлетворения граничным условиям на краях оболочечной части подвеса.

- сформулированы граничные условия для поплавкового подвеса, края которого свободны от закреплений. Выполнены операции разделения переменных в граничных условиях в соответствии с исходными предпосылками метода Фурье.