Карачун В.В., Мельник В.Н.
Национальный технический университет Украины «КПИ»
КООРДИНАТНЫЕ ФУНКЦИИ ОБОЛОЧКИ ПРИ УСЛОВИИ ЛИНЕЙНОЙ
НЕЗАВИСИМОСТИ КАЖДОЙ ПАРЫ
Координатные функции оболочки с ненулевой Гауссовой кривизной можно
представить в виде:


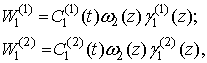
где
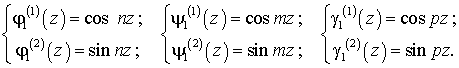
Для вычисления координатных функций поплавка можно
воспользоваться формулами Крамера и найти величины ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
С этой целью системы уравнений запишем в общем виде:
.
С этой целью системы уравнений запишем в общем виде:
 (1)
(1)
 (2)
(2)
Характеристический определитель ![]() системы (1) представлен выражением –
системы (1) представлен выражением –
![]() (3)
(3)
а
определитель ![]() системы уравнений (2) имеет вид:
системы уравнений (2) имеет вид:
![]() .
.
Тогда из (1) можем найти искомые неизвестные:
![]() (4)
(4)
где
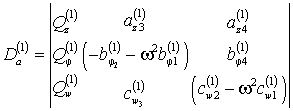 ; (5)
; (5)
 ; (6)
; (6)
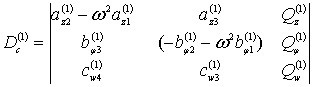 . (7)
. (7)
Аналогично из (2):
![]() (8)
(8)
где
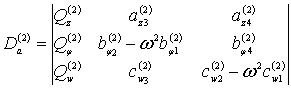 ; (9)
; (9)
 ; (10)
; (10)
 . (11)
. (11)
Вычислим частные определители:
![]()
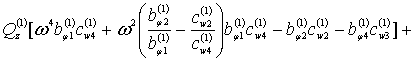
![]() (12)
(12)
![]()
![]()
![]() (13)
(13)
![]()
![]()
![]() (14)
(14)
![]()
![]()
![]()
![]() (15)
(15)
![]()
![]()
![]() (16)
(16)
![]()
![]()
![]()
![]() (17)
(17)
Итак, выполнена вся подготовительная работа, позволяющая
для каждого конкретного случая установить закономерности упругого перемещения
поверхности поплавка гироскопа.