Математика/ 5. Математическое моделирование

Айнабек Е.Е., к.ф.-м.н. Искакова А.С.

Казахско-турецкий лицей г. Петропаловск, Казахстан

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Модернизация прогнозов доходов букмекерских контор

По статистической отчетности определенной букмекерской конторы имеем статистические данные за последние k временных периодов доходов и операционных расходов. Под понятием дохода принято выбирать сущность ставки, то есть денежная сумма или плата за игру, которую Игрок обязан внести в букмекерскую контору в порядке и сроки, предусмотренные Правилами. Соответственно операционные расходы – это, так называемые, выплаты букмекерской конторой Игроку денежных выигрышей. Нас интересует, как выглядит функциональная зависимость между x_i и y_i, где i принимает любые натуральные конечные значения.

Пусть y – функция одной переменной с двумя параметрами a и b. В качестве набора выбора функций, из которых будем иметь эмпирическую зависимость, рассмотрим: линейную функцию ; показательную функцию ; дробно-рациональную функцию ; логарифмическую функцию ; степенную функцию ; гиперболическую функцию 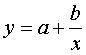; дробно-рациональную .

Для наилучшего выбора вида аналитической зависимости y=f(x,a,b) выстраем следующие промежуточные вычисления. На заданном отрезке изменения независимой переменной выбирают точки, достаточно надежные и, по возможности, далеко отстоящие друг от друга. Будем считать, что это x₁ и x_k.

Вычислим среднее арифметическое ,среднее геометрическое и среднее гармоническое .По вычисленным значениям независимой переменной находим из статистических данных таблицы 1 соответствующие значения переменной , , для пока еще неизвестной аналитической зависимости y=f(x,a,b).

Вычислим среднее арифметическое крайних значений , среднее геометрическое и среднее гармоническое 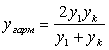. В итоге после проделанных вычислений оцениванием следующие погрешности:

, , , ,

, , .

Следующая теорема позволяет определить приближение к функциональной зависимости статистических данных финансовых активов страховой компании.

Теорема. Пусть . Тогда

1. если e=e₁, то в качестве аналитической зависимости для данного графика хорошим приближением служит линейная функция ;

2. если e=e₂, то в качестве аналитической зависимости для данного графика хорошим приближением служит показательная функция;

3. если e=e₃, то в качестве аналитической зависимости для данного графика хорошим приближением служит дробно-рациональная функция ;

4. если e=e₄, то в качестве аналитической зависимости для данного графика хорошим приближением служит логарифмическая функция;

5. если e=e₅, то в качестве аналитической зависимости для данного графика хорошим приближением служит степенная функция:

6. если e=e₆, то в качестве аналитической зависимости для данного графика хорошим приближением служит гиперболическая функция

7. если e=e₇, то в качестве аналитической зависимости для данного графика хорошим приближением служит дробно-рациональная функция .

Таким образом, из выше предложенной теоремы определяется вид эмпирической функции f(x,a,b). Коэффициенты a и b эмпирической функции f(x,a,b), можно определить несколькими способами, оптимальным из которых является метод наименьших квадратов. Согласно методу наименьших квадратов коэффициенты a и b должны удовлетворять следующему равенству

Следовательно, коэффициенты a и b, получаемые по методу наименьших квадратов, должны удовлетворять следующей системе уравнений

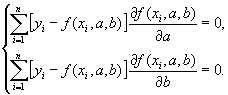(1)

Как видно, что система уравнений (1) имеет не сложное решение, если вид эмпирической функции представляет собой линейную зависимость (). То есть, если , то система уравнений (1) имеет вид

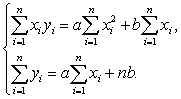(2)

Значит, если эмпирическая функция не является линейной зависимостью, то для удобного использования метода наименьших квадратов, необходимо свести к линейной зависимости. Рассмотрим, как нелинейные зависимости преобразованием координат можно свести к линейной.

1. Для показательной зависимости вида , логарифмируя имеем . Полагаем lgy=z, x=q, , и в плоскости qOz получим уравнение прямой z=Bq+A.

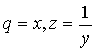2. Для дробно-рациональной функции , введем новые переменные ; тогда получим зависимость вида

3. Для логарифмической функции ; введем новые переменные ; тогда получим зависимость вида

4. Для степенной функции ; введем новые переменные ; тогда получим зависимость вида

5. Для гиперболической функции , введем новые переменные ; тогда получим зависимость вида

6. Для дробно-рациональной функции , введем новые переменные ; тогда получим зависимость вида

Литература:

1. Данилина Н.И. и др. Численные методы.

2. Малыхин В.И. Финансовая математика. –М.:Юнити, 2003. -237 с.

3. Волков И., Загоруйко Е. Исследование операций. М-2002.

4. Искакова А.С. Условие существования оценок максимального правдоподобия для параметров одного класса многомерных распределений // Известия МОН РК, НАН РК. 2004 г. №1. – С. 90-95.

5. Искакова А.С. Об определении некоторых оценок одной вероятностной модели // Евразийский математический журнал. -2005, №2.- С. 87-101.