12руснаука2

к.ф.-м.н. А.И. Долгарев

РЕДУКЦИЯ К КАНОНИЧЕСКИМ ЕВКЛИДОВЫМ КРИВЫМ

В ЕСТЕСТВЕННОЙ ПАРАМЕТРИЗАЦИИ

По заданной функции кривизны и кручения евклидовой линии указано ее естественное параметрическое представление. Плоская линия является совокупностью малых дуг соприкасающихся окружностей, пространственная – совокупностью дуг винтовых линий. Указаны эти совокупности по заданным кривизнам. По заданным скалярным функциям кривизн линии получено векторное задание линии в окрестности данной точки.

К каноническим кривым относятся кривые постоянных кривизн. Редукция к канонической кривой позволяет по заданным кривизне и кручению получить отыскиваемую линию в окрестности точки. В плоском случае линия апроксимируется дугами соприкасающихся окружностей, в пространственном – дугами винтовых линий.

1. Плоские линии

1.1. Кривизна плоской кривой

Плоская регулярная класса евклидова кривая может быть задана в естественной параметризации

= , ,

где интервал числовой оси . Модуль вектора касательной во всякой точке кривой равен 1:

; (1)

кривизна линии вычисляется по формуле

. (2)

Радиус кривизны линии в каждой точке есть .

В произвольной параметризации

= ,,

кривизна линии вычисляется по формуле

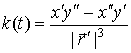. (3)

Величина кривизны линии в каждой ее точке от параметризации не зависит.

Известно, что линия однозначно, с точностью до положения на плоскости, определяется заданной функцией кривизны

, (4)

см., например, [1, c. 137 – 144]; функция (4) называется натуральным уравнением линии. Иными словами, по скалярной функции кривизны (4) линии однозначно определяется естественная параметризация линии .

Евклидова плоская линия ненулевой постоянной кривизны является окружностью, она может быть описана векторной функцией,

= , (5)

параметризация не является естественной, т.к. . Дифференциал длины дуги линии (5) есть , поэтому . При окружность (5) имеет естественную параметризацию = . В этом случае ее кривизна равна , радиус есть .

1.2. Естественная параметризация окружности

Окружность по натуральному уравнению

Установим вид параметрического задания окружности, имеющей кривизну , в случае естественного параметра.

1. Лемма. В естественной параметризации окружность кривизны описывается векторной функцией

= , ; (6)

радиус окружности равен .

# Пусть окружность задана функцией

= , .

Найдем значения величин . Производные функции (6) таковы:

= , = .

Модули производных заданной функции равны

, .

Потребовав выполнения условия (1), находим

. (7)

В этом случае . Кроме того,

= .

По условию, кривизна окружности (6) равна , поэтому

.

Тогда в (7)

=.

Следовательно, в естественной параметризации окружность записывается функцией (6). Вычисляя кривизну окружности по формуле (3), находим

= ,

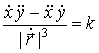что еще раз подтверждает естественность параметра в (6). #

В конце предыдущего п. 1.1 получена другая естественная параметризация окружности и значение кривизны другое.

Например, для окружности в параметризации (5) :

, =.

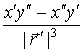Результат закономерный: радиус окружности равен и кривизна равна . Однако, по формулам (2) и (3) значения получены различные, что тоже закономерно для параметризации, не являющейся естественной.

Параметризация (6) тривиально исчерпывающе характеризует окружность: в записи (6) наличествует кривизна и радиус .

2. Лемма. Если задана кривизна окружности , то параметрическое задание окружности есть (6), лемма 1.

# По (2) имеем дифференциальное уравнение

.

Уравнению удовлетворяют следующие функции, см. лемму 1, (с учетом (6)):

, .

Интегрируя эти равенства дважды и выбрав нулевые значения постоянных интегрирования, приходим к функции (6). #

1.2. Отыскание параметрического представления

произвольной линии по функции кривизны

В [1] параметрическое представление линии по натуральному уравнению получено в естественной параметризации. И (6) есть естественная параметризация окружности, найденная по натуральному уравнению .

Пусть теперь в (4) дифференцируемая функция. Укажем естественную параметризацию линии по заданному уравнению (4).

3. Теорема. Если задана дифференцируемая функция (4), то в естественной параметризации линия с кривизной (4) имеет вид , где

, , (8)

причем

. (9)

Начальные условия вида

, (10)

определяют единственную линию, проходящую через данную точку в направлении данного единичного вектора .

# Компоненты векторной функции ищем по условию, см. доказательство леммы 2,

.

Согласно этому условию по лемме 1 положим:

, , (11)

где есть (9). Так как

,

то первые интегралы разыскиваемых функций таковы

, (12)

. (13)

Функции (12) и (13) при обладают свойством

,

таким образом, для функции = выполняется . Теперь компонентами разыскиваемой функции являются функции (8). По (11), (12) и (13) при находим . Свойства функций указывают на то, что параметризация разыскиваемой линии является естественной.

Значения постоянных интегрирования в (12) и (13) выделяют по одной из функций из получаемых классов функций, что приводит к отысканию компонент функции .

Начальные условия (10) позволяют получить линию заданной кривизны, проходящую через точку . #

Функции (8) в общем случае являются неэлементарными. Они относятся к синус-интегралам и косинус-интегралам. Среди них содержатся функции Френеля и Фурье. Но (8) не исчерпываются функциями Френеля и Фурье.

Пример. Не всегда синус-интегралы и косинус-интегралы неэлементарны. Пусть . По (2): . Согласно (9), . По (8), имеем:

, .

Следовательно, на основании (12), соответственно (13) , получаем

, .

Заменяя , приходим к интегралам

= , .

Значит,

, .

Для полученной линии имеем при .

1.4. Локальные свойства плоских регулярных кривых

Пусть регулярная кривая , имеющая функцию кривизны (4), параметризована функциями (8). Во всякой точке линии , соответствующей значению , кривизна линии равна . В малой окрестности точки кривизну линии можно считать постоянной и равной . В этой окрестности линия описывается в виде (6):

= .

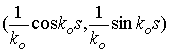Здесь не учтены координаты центра кривизны. Таким образом, в рассматриваемой окрестности линии совпадает с соприкасающейся окружностью. В параметризации этой окружности указан ее радиус , являющийся радиусом кривизны в точке . Линия представляется множеством малых дуг соприкасающихся окружностей вида (6).

Например, если кривизна линии есть

, ,

то, согласно теореме 3, линия задается в виде

,

каждая компонента в задании линии представляется проинтегрированным степенным рядом, полученным по разложениям функций синуса и косинуса

, .

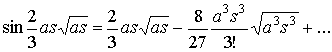Ряды сходятся для всех . Во всякой точке имеется соприкасающаяся окружность

= .

Если нужна линия только в окрестности некоторой точки, то можно довольствоваться последней функцией (учтя координаты центра кривизны).

2. Пространственные линии

2.1. Кривизна и кручение пространственной кривой

Регулярная кривая класса евклидова пространства в произвольной параметризации описывается векторной функцией

= , . (14)

В теоретических вопросах используется естественная параметризация

= , , (15)

параметр есть длина линии от некоторой ее точки. Интервалы в заданиях (14) и (15) линии не обязательно совпадают. Дифференциал длины линии , заданной в параметризации (14), вычисляется по формуле

. (16)

На линию (14) налагается условие . В естественной параметризации

(17)

и кривизна линии определяется следующим образом:

. (18)

Кручение кривой в естественной параметризации отыскивается по формуле

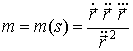. (19)

Кривизна и кручение кривой не зависит от ее параметризации; в произвольной параметризации (14) вычислительные формулы таковы

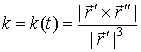, . (20)

Пространственная евклидова линия с постоянными ненулевыми кривизнами , является винтовой линией

= . (21)

Радиус цилиндра, не который намотана винтовая линия, равен , шаг винтовой линии равен . Кривизна и кручение винтовой (20) равны

, . (22)

У линии (21) модуль вектора касательной есть

. (23)

2.2. Винтовая линия по натуральным уравнениям

Получим винтовую линию в естественной параметризации, кривизна которой равна и кручение равно .

4. Теорема. В естественной параметризации винтовая линия кривиз-

ны и кручения описывается векторной функцией

= . (24)

# Для функции (20) найдем выражения через заданные величины , и величину . По (16):

; = .

Считаем . Значит, . По значениям (22) имеем ; тогда

.

Согласно (18), , поэтому

, .

Подставляя найденные значения в (21), получаем (24). #

Легко убедиться, что с использованием (18), (19), а также формул (21), значения кривизны и кручения линии (24) равны соответственно , .

4. Теорема. Если заданы кривизна и кручение равно вин-

товой линии , то функции задания (15) винтовой линии являются решениями системы обыкновенных дифференциальных уравнений

(25)

Начальные условия вида

;

, ;

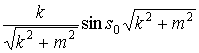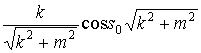,;(26)

,

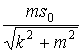определяют единственную линию, проходящую через точки направлении вектора .

# Кривизна винтовой линии в естественной параметризации, согласно (16), удовлетворяет соотношениям

, .

По виду первого из этих уравнений можно записать

, .

Отыскиваемая линия является винтовой, имеет естественную параметризацию, поэтому она описывается функцией (24). Коэффициент , согласно (24), равен . Таким образом, приходим к системе обыкновенных дифференциальных уравнений (25). В результате интегрирования указанных уравнений имеем

, ,

.

Начальные условия (26) дают винтовую линию в виде (24).

Первая производная полученной функции (24) такова:

,,.

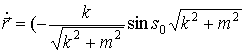Находим: , см. (17). Кривизна и кручение линии (24), вычисленные по формулам (18), (19), а также по формулам (20), дают один и тот же результат: кривизны равны заданным числам . #

2.3. Пространственная кривая в естественной параметризации

в локальном задании

Известно, что регулярная пространственная евклидова линия с точностью до положения в пространстве определяется функциями кривизны и кручения, [1, c. 196 – 208]. В каждой своей точку регулярная пространственная кривая имеет конкретные значения кривизны и кручения ; в окрестности каждой точки кривая обладает соприкасающейся винтовой линией. С движением точки по линии изменяется ее кривизна и кручение и соприкасающаяся винтовая линия. По заданным функциям кривизны и кручения имеем для каждого значения соответствующую винтовую линию, являющуюся соприкасающейся для кривой с заданными функциями кривизны и кручения. Поэтому справедлива

6. Теорема. Если заданы функции , , то про-

странственная линия = определяется в результате решения системы обыкновенных дифференциальных уравнений

(27)

и функцией .#

По этой теореме, всякая регулярная пространственная кривая представляется системой дуг винтовых линий.

Заметим, что в решении уравнений системы (27) имеются синус-интегралы и косинус-интегралы, они сложнее функций (12) и (13). Здесь удобнее воспользоваться представлением (24), где , .

Теоремы 3 и 6 позволяют по заданным скалярным функциям кривизн линии получить векторное задание линии в естественной параметризации в окрестности данной точки.

Литература

1. Рашевский П.К. Курс дифференциальной геометрии. – М.: Гостехиздат, 1956. – 420с.