MATHCAD В ЗАДАЧАХ ТЕОРИИ УПРАВЛЕНИЯ.
Капалин В.И., Шаповалова Н.Е.
Москва,
МИЭМ НИУ ВШЭ.
Система компьютерной математики Mathcad
обладает широкими возможностями для численных и символьных вычислений, а также
мощными графическими возможностями, реализованными посредством удобного и наглядного
интерфейса. Это позволяет её использовать при исследовании устойчивости
систем и при решении задач теории управления частотными методами.
Ключевые слова:
Mathcad, теория управления, частотные методы.
Mathcad in control theory. Kapalin V.I.,
Shapovalova N.E., Moscow, MIEM HSE. The system of computer
mathematics Mathcad has wide opportunities for numerical and symbolic
computation, as well as powerful graphics capabilities, implemented through an
easy and intuitive interface. This allows its use in stability analysis of
systems and for solving problems of the theory of frequency control methods.
Key words: Mathcad, control theory, frequency domain methods.
За последнее время широкое распространение
получили системы компьютерной математики, такие как Maple компании Waterloo Maple Inc., Mathematica компании
Wolfram Research,
MATLAB компании
MathWorks и Mathcad, принадлежащая компании PTC. В процессе преподавания теории управления в крупных
технических университетах мира обычно используется система MATLAB — наиболее распространенная
и обширная [1]. Эта система сделала теорию управления значительно более
ясной и доступной для изучения. Однако, эта, исторически сложившаяся
ситуация, не может рассматриваться как единственно возможная. Недостатки
MATLAB хорошо известны — не самый удобный для пользователя интерфейс командного
окна, большой объем памяти, занимаемый программой при установке на
компьютер полной версии и наличии расширений, которые предназначены для узких
специалистов и не используются в теории управления. Наконец, высокая стоимость MATLAB
делает проблематичным её приобретение для многих технических университетов
РФ.
В указанной связи в вузах РФ в качестве
альтернативы MATLAB стала рассматриваться значительно более компактная и более
удобная для учебных приложений система Mathcad [2]. Система Mathcad обладает интерфейсом, который
действительно можно назвать "дружественным". Формулы записываются в
любом месте рабочего листа, практически в своей обычной форме. Для построения
графиков не нужно изучать специальных операций с массивами, как в MATLAB.
Графики строятся не в отдельном графическом окне, а в том месте на рабочем
листе, которое указывается пользователем. Если в процессе работы вносятся изменения
во введенные формулы, то все последующие численные результаты автоматически
пересчитываются, а графики — перестраиваются.
Наконец, Mathcad гораздо более терпимо, "дружелюбно" относится к
неизбежным ошибкам пользователя при вводе формул и не делает, например,
глобальной проблемы, как MATLAB, если вместо точки по недосмотру введена
запятая. Все эти преимущества Mathcad оказываются очень привлекательными для
студентов технических университетов, которые часто изучают основы работы в
Mathcad самостоятельно.
Система Mathcad имеет два ядра — цифровое
и символьных операций. Поэтому в Mathcad легко реализуется основной
математический аппарат теории непрерывных и дискретных систем управления —
преобразования Лапласа, Фурье и Z-преобразование [3]. Наличие
обычной двумерной графики и графики в полярных координатах позволяет
реализовать классические частотные методы теории систем управления.
Как это ни странно, но одним из достоинств
Mathcad с педагогической точки зрения является отсутствие в системе встроенных
команд для реализации методов теории управления, в отличие от системы MATLAB.
Следствием этого обстоятельства является то, что для применения того или иного
метода теории управления пользователь — студент должен точно ввести
соответствующие формулы. При этом небольшие документы, такие как, например,
студенческие лабораторные и курсовые работы можно оформлять непосредственно в
Mathcad при помощи возможностей работы с текстом, не прибегая к средствам Microsoft
Word или других текстовых редакторов.
Частотные критерии устойчивости в Mathcad
реализуются так, как показано на следующих рисунках. На рис. 1 и
рис. 2 приведены графики годографа Михайлова для случаев устойчивой и
неустойчивой систем третьего порядка.
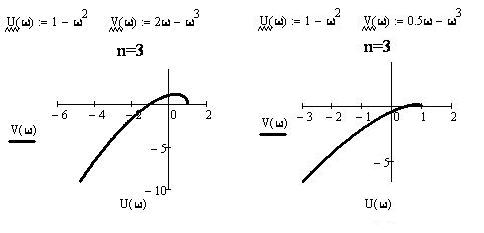
Рис. 1.
Рис. 2.
Критерий устойчивости Найквиста для
случаев устойчивой и неустойчивых систем в замкнутом состоянии реализуется
так как показано на рис. 3 — рис. 5.
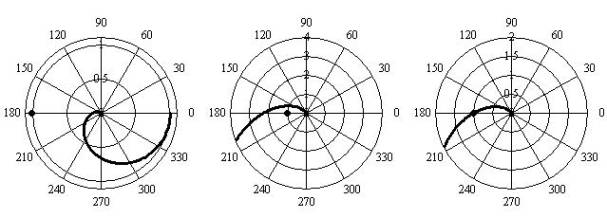
Рис. 3. Рис. 4. Рис.
5.
Частотные характеристики — амплитудная,
фазовая, логарифмическая и асимптотическая логарифмическая в Mathcad для
случая колебательного звена приведены на рис. 6 — рис. 8.
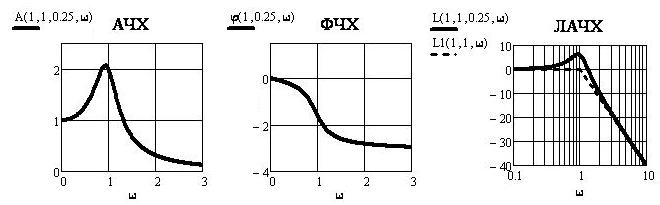
Рис. 6. Рис.
7. Рис.
8.
Частотный синтез замкнутой системы
управления в Mathcad можно осуществить с помощью окружностей Холла, графики
которых приведены на рис. 9.
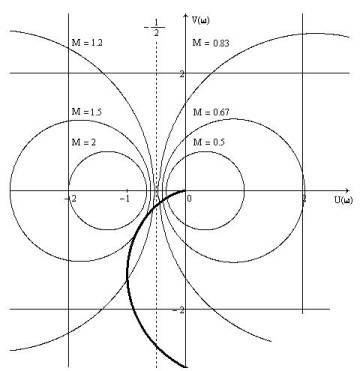
Рис. 9.
Для астатической системы с передаточной
функцией объекта управления 
при 
, и 
, при показателе колебательности 
, подберем соответствующее значение коэффициента усиления — 
из диаграммы Холла
и годографа Найквиста — рис. 10.
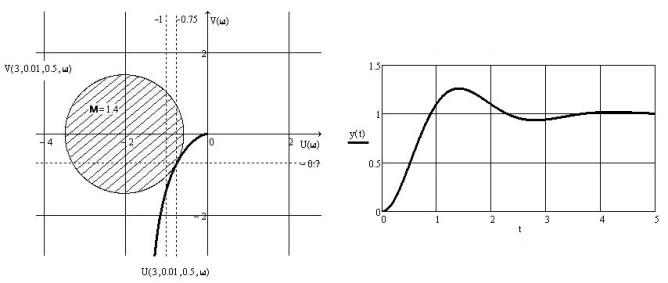
Рис. 10. Рис.
11.
Соответствующий график переходного
процесса для замкнутой системы, построенный в Mathcad, приведён на рис. 11.
Синтезированная система с обратной связью,
как это следует из приведенного графика переходной характеристики,
обладает желаемыми показателями качества.
Литература.