Экономические науки/8. Математические методы в экономике

К.т.н. Лясковский А.В.

Одесская национальная академия пищевых технологий, Украина

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ АССОРТИМЕНТОМ ПРОДУКЦИИ ПРЕДПРИЯТИЯ НА ЭВМ

Актуальность адаптивного управления товарным ассортиментом производственного предприятия определяется тем, что оно позволяет обеспечить сохранение работоспособности управляемого объекта, при непредвиденных изменениях его свойств, целей управления или окружающей среды, на основе изменения алгоритма функционирования или поиска оптимальных состояний.

Предлагаемая концепция оптимального управления ассортиментом продукции, базируется на следующих принципах. Ассортимент продукции предприятия в своем развитии проходит две стадии. Первая стадия состоит в формировании производственного ассортимента и связана с созданием потребительской ценности, соответствующей потребностям целевого рынка и превышающей конкурирующие аналоги. Вторая стадия заключается в преобразовании производственного ассортимента в товарный ассортимент, в соответствие с каналами распределения, ценовой и коммуникативной политикой.

Сложность управления ассортиментом определяется наличием многовариантности использования различных видов сырья для выпуска продукции. Дополнительные затруднения вносят объективные факторы, вызванные функционированием предприятия в рыночной экономике, в условиях конкуренции, дефицита финансовых ресурсов и низкой платежеспособности населения. Данные обстоятельства вызывают необходимость рассматривать управление ассортиментом продукции - как сложный процесс, требующий постоянного и многократного пересчета в сжатые временные сроки, с учетом изменившейся ситуации рыночного спроса.

В этих условиях, традиционные методы нормативно-балансового планирования не позволяют качественно решить данную проблему, что определяет актуальность использования математических методов и вычислительной техники. Правильное решение этой проблемы может быть обеспечено только на основе применения экономико-математических методов и ЭВМ, которые позволят оперативно формировать оптимальный, сбалансированный по ресурсам и затратам ассортимент продукции. Это позволит оперативно вносить необходимые корректировки, что обеспечит гибкое и мобильное управление.

В качестве аналитического инструмента, описывающего процесс формирования ассортимента продукции, использована следующая двухэтапная математическая модель. На первом этапе, производится формирование производственного ассортимента с помощью модели, позволяющей определить объемы выпуска продукции Х1, Х2, …, Хn, обеспечивающие максимум прибыли:

maxF(x) =

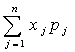
где Xj - обьем производства j- го вида продукции;

Pj- прибыль на единицу выпуска j-го вида продукции.

При этом, объемы производства j-го вида продукции Хj не должны быть больше спроса, суммарный выпуск не может превышать номинальной мощности предприятия, а использование сырья не должно превышать имеющихся запасов.

На втором этапе производится преобразование производственного ассортимента в товарный ассортимент. С этой целью, исходные данные представляются в так называемой «игровой матрице», в которой участвуют две стороны, называемые в теории игр - «игроками». Первая сторона - это предприятие, выпускающая продукцию, вторая сторона - потребители, спрос которых удовлетворяется данной продукцией. В процессе решения задачи предполагается, что интересы сторон могут быть противоположны. При этом возможны ситуации, когда деятельность одной из сторон направлена на уменьшение выпуска продукции, с целью обеспечения его полной реализации, а деятельность другой стороны направлена на увеличение выпуска. Противоположность интересов в деятельности сторон приводит к образованию конфликтных ситуаций, для исследования которых применяется математическая теория игр. С этой целью в игровой матрице формируются значения остатков нереализованной продукции, характеризующих выигрыш конкурентов на рынке, а также неудовлетворенный спрос на продукцию, определяющий возможный выигрыш производителя. В результате, определяются все возможные планы игры (или стратегии) каждой из сторон.

Для практического решения данной задачи и определения оптимальных стратегий каждой из сторон и нахождения, так называемой «седловой точки» игры, используются классические критерии теории игр, называемые «минимаксом» и «максимином». Нахождение «седловой точки» равносильно стандартной задаче линейного программирования, которая решается на ЭВМ с использованием инструмента «Поиск решения» процессора EXCEL.

Применение ЭВМ позволяет осуществить имитационное моделирование экономического процесса, что позволяет задавать в диалоговом режиме различные значения параметров и оценивать результаты решения. Практический опыт использования предлагаемых моделей при формировании ассортимента продукции предприятия, показывал возможность увеличения прибыли на 5-7%