Исавнин
А.Г.
Камская государственная
инженерно-экономическая академия,
Набережные Челны,
Россия.
Моделирование убытка при перестраховании с пропорциональным делением риска
В последнее время
индустрия страхования в России претерпевает рост, о котором можно судить по
увеличению количества страховых компаний, предоставляющих свои услуги по
различным видам страхования. В условиях рыночной конкуренции как никогда важен
вопрос о повышении привлекательности страховых договоров для потребителя,
которой можно достичь, предлагая более выгодные условия, чем у конкурентов, и в
то же время ещё важнее вопрос о сохранении страховой компанией устойчивых
позиций на рынке, снижении вероятности разорения.
Страхование основывается
на так называемом коллективном балансе. Подразумевается, что объединение
(портфель) нескольких рисков, не являющихся полностью положительно
скоррелированными, имеет более выгодные распределение убытка и размер премии,
чем каждый отдельный риск, поскольку в коллективе благоприятные и
неблагоприятные (в сравнении с индивидуальным ожиданием) процессы убытков
отдельных рисков могут взаимно компенсироваться.
Но на практике страховые
портфели всегда ограничены по объему и остаются зависимыми от случайности,
несмотря на коллективный баланс и закон больших чисел. Более того, абсолютный
разброс совокупного убытка вокруг своего математического ожидания увеличивается
с ростом объема портфеля, хотя и медленнее, чем само математическое ожидание.
Даже если бы все распределения были известны, совокупный убыток по-прежнему
оставался бы недетерминированным – в этом заключается риск случайности. Математическое ожидание совокупного убытка
неизвестно ни для одиночного риска, ни для портфеля и должно оцениваться на
основании статистики. Получаемая оценка в той или иной мере всегда отклоняется
от истинного значения. Этот источник неопределенности называется риском оценки. Возможность точного
диагностирования случайной закономерности прошлого не исключает угрозы
частичного изменения этой закономерности в ближайшем будущем. А так как премия
всегда устанавливается заранее, возникает третий источник неопределенности – риск прогноза. Все три источника
неопределенности действуют вместе и называются техническим страховым риском. То есть коллективный баланс не
избавляет страховую компанию от риска, хотя
и уменьшает риски, связанные с оцениванием и случайностью.
Чтобы
снизить технический риск, страховая компания может прибегнуть к перестрахованию
– процессу распределения риска
между несколькими компаниями.
Для расчета страховых, в том числе перестраховочных, тарифов и премий
требуется знать распределение величины убытка, а также необходимо
иметь сведения о характере страхуемых рисков. Встает проблема моделирования
размеров конкретных убытков. Дело в том, что риски в портфеле в большинстве
случаев имеют неоднородную структуру, а используемые в теории «индивидуальные»
модели предназначены в основном для моделирования математического ожидания и
дисперсии совокупного годового убытка однородной группы рисков.
Возникает
мысль разбить портфель на максимально однородные и независимые группы,
построить для каждой из них распределение совокупного убытка в соответствии с
индивидуальной моделью, а затем свернуть полученные распределения к
распределению совокупного убытка портфеля. Поскольку свертка различных
распределений не задается без помощи интеграла, этот путь не дает
аналитического решения, хотя вполне осуществим при помощи численных методов.
Однако из-за требования однородности некоторые группы могут оказаться настолько
мелкими, что достоверно описать хвосты распределении индивидуальными моделями
не удастся, как и проверить адекватность модели в области хвоста или подобрать
подходящую модель. Эта проблема типична для рисков с высокими страховыми
суммами, число которых сравнительно невелико, а влияние на распределение убытка
совокупного портфеля существенно.
Другой,
гораздо более успешный путь был указан в начале XX столетия шведом Филиппом
Лундбергом и продолжен его соотечественником Гаральдом Крамером. Речь идет о
так называемой коллективной модели, ставшей отправной точкой новой дисциплины в
рамках теории вероятностей – «коллективной теории риска». Идея коллективной модели – рассматривать
портфель только как производителя убытков, не учитывая принадлежность убытков
конкретным рискам. Справедливо задать вопрос, не отражается ли потеря
информации на качестве результата? Оказывается, что нет. Дело в том, что параметры
исходных распределений коллективной модели (распределения размера убытка),
могут быть оценены значительно точнее, чем для распределения убытков отдельных
однородных групп рисков.
Пусть N
— случайное число страховых событий, происходящих в определенном
фиксированном временном промежутке (например, в предстоящем календарном году) и относящихся к
портфелю рисков (например, совокупность рисков страхования автогражданской
ответственности). Тогда при выполнении довольно общих предпосылок N имеет распределение Пуассона
с параметром 
. Перечислим эти предпосылки:
1.
случайные
величины числа убытков в двух непересекающихся подынтервалах рассматриваемого
временного промежутка независимы.
2.
одновременно
не могут произойти два и более убытка (регулярность так называемой функции
интенсивности),
3.
убытки
могут происходить в любые моменты времени (непрерывность функции
интенсивности).
Есть еще одна предпосылка, связанная с
распределением Пуассона, а именно стационарность процесса наступления убытков.
Но для построения распределения Пуассона на фиксированном временном
промежутке это требование не обязательно, потому что мы заранее
отказываемся от нереалистичного предположения однородности процесса убытков внутри рассматриваемого временного
промежутка и исходим из неоднородного процесса Пуассона. Этим допускается
возможность различия частоты убытков днем и ночью или зимой и летом.
Обычно считается, что фактические риски страхователей эквивалентны
рискам, составляющих портфель страховой компании. На самом деле это
не совсем правильно. Страховая компании часто принимает риск не
полностью, а только
частично и, в свою очередь, сама передает часть принятых рисков.
При пропорциональном
делении риска величина убытка X (размер
убытка в одном страховом случае или совокупный убыток за год)
делится на две части 
и 
по правилу:
В этом случае обе части всегда содержат убыток. Каковы же
причины деления риска между страховщиком и
перестраховщиком? Вероятность
выполнения обязательств перед страхователями
определяется
суммарной нетто-премией b, распределением совокупного убытка G и
гарантийным капиталом с. Посчитав
недостаточной надежность 
, компания сама может приобрести
страховую защиту в
другой страховой компании или в предназначенной специально для этой цели
перестраховочной компании. Замена части взятых на себя страховщиком неизвестных расходов по убыткам на
фиксированные расходы называется перестрахованием.
Этот способ сокращения риска, как правило, проще альтернативных
способов, таких как увеличение премиального фонда, пополнение гарантийного капитала или улучшение
распределения совокупного убытка (например, за счет изменения условий
страхования пли отказа от некоторых рисков),
и позволяет страховщику принимать особо крупные риски, заведомо нарушающие баланс портфеля. В то же время можно сказать,
что перестрахование стимулирует заключение договоров страхования и в этом смысле
равносильно повышению гарантийного капитала. Каждая страховая компания,
предоставляющая страховую защиту другой страховой компании, в этой связи
называется перестраховщиком, а компания, выписывающая первичные полисы,
– страховщиком. На практике почти каждая страховая компания заключает
договоры перестрахования с одним или несколькими перестраховщиками.
Перестраховщик не имеет договорных отношений со страхователями, чьи полисы он
перестраховывает, и страхователи не знают, перестрахованы они или нет.
Назначение премий и урегулирование убытков по всем полисам, включая
перестрахованные, полностью входит в обязанность страховщика.
В принципе, страховщик и
перестраховщик могли бы договариваться о форме и объеме перестрахования по
каждому полису в отдельности. Некоторые крупные риски именно так и делятся
между несколькими страховыми компаниями (факультативное перестрахование). Но в
подавляющем большинстве случаев перестрахование осуществляется в рамках
договора между страховщиком и перестраховщиком, действующего для всех рисков,
составляющих портфель страховщика в течение установленного срока (облигаторное
перестрахование). В договоре четко прописано, какую часть, каких рисков или
убытков несет перестраховщик, и какую премию он за это получает. Обычно для
удобства договоры перестрахования заключаются на один год отдельно для каждого
вида страхования.
Формы пропорционального
перестрахования.
1. Квотное перестрахование. Перестраховщик
принимает от всех полисов фиксированную одинаковую процентную долю, например
50%, то есть возмещает 50% от каждого убытка и получает 50% от каждой премии
(рисунок 1) (за вычетом доли расходов на привлечение клиентов и
административных расходов – так называемой перестраховочной комиссии).
Рисунок 1.
Распределение риска при пропорциональном перестраховании
Таким образом, 50% от совокупного
годового убытка и суммарной годовой премии страховщика переходят к
перестраховщику.
2.
Перестрахование эксцедента сумм. Если при квотном перестраховании все
риски делятся между страховщиком и перестраховщиком в одинаковой пропорции 
, то при перестраховании эксцедента сумм собственное
удержание варьируется в зависимости от страховой суммы v по правилу 
. Иными словами, страховщик полностью оставляет себе риски
со страховой суммой 
и делит с
перестраховщиком риски со страховой суммой, превышающей 
. При этом перестраховщик принимает часть, соответствующую
разности между страховой суммой и 
, Скажем, если в договоре перестрахования установлено
значение 
=1 млн., то от риска со страховой суммой v=4 млн.
перестраховщик принимает 75%. В
остальном все совпадает с квотным перестрахованием: по риску со страховой
суммой v премия и
убытки
делятся
между страховщиком и перестраховщиком в соотношении 
к 
. Таким
образом, речь идет о чисто пропорциональном делении риска, но собственное удержание не
пропорционально страховой я сумме 
. Перестрахование эксцедента сумм способствует
гомогенизации страховых сумм в портфеле
страховщика. Обычно по условиям договора
перестрахования часть страховой суммы, принимаемая перестраховщиком, ограничивается значением 
. Тогда перестраховщик принимает от каждого риска со страховой суммой 
не долю 
, а
,
где
, как правило, целое число. Благодаря этому перестраховщик
уже при заключении договора знает, что
его расход по отдельному убытку в любом случае не превысит 
.
Рассмотрим, как влияет деление риска на
основные случайные величины – характеристики убытка. С делением риска связаны две основные задачи.
Во-первых, необходимо выяснить, как влияет деление риска па премию, ведь
непропорциональное деление изначально определяется только как деление убытков.
При пропорциональном делении риска этот вопрос не ставится – здесь сразу задано
правило деления договоров страхования, то есть премий и убытков. Во-вторых, не
менее важно знать, какая форма деления риска наиболее целесообразна в
конкретном случае и насколько велика должна быть отдаваемая часть.
При пропорциональном
делении риска 
случайные
величины Х, сХ, (1–с)Х отличаются только
«масштабами», равными соответственно 1,
с, (1–с), и преобразование интересующих нас параметров риска особых
сложностей не вызывает. Так, в распределении
числа убытков абсолютно ничего не меняется.
Распределение пропорционально уменьшенного размера убытка сХ непосредственно находится из распределения 
оригинального размера убытка, в силу равенства 
. Плотность 
величины сХ
и плотность f величины X связаны
формулой 
. Как видим, вид плотности
полностью сохраняется, изменяется только масштаб. Если для F принята
некоторая модель распределения (например, логнормальное распределение), то
в результате пропорционального деления риска меняется только скалярный
параметр, а параметр
формы остается прежним. Из соотношений
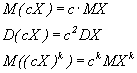
непосредственно
следует, что относительные меры риска: коэффициент вариации 
и асимметрия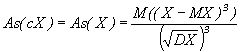 
при пропорциональном
делении риска не изменяются. В этом состоит важнейшее свойство пропорционального
деления риска. Все приведенные утверждения о
поведении распределения и его параметров справедливы при квотном
перестраховании в отношении совокупной
переданной в перестрахование части портфеля.
При
перестраховании эксцедента сумм зависимость пропорции деления 
от страховой суммы v способствует уменьшению
относительного риска (измеряемого коэффициентом вариации и асимметрией) в
портфеле страховщика и увеличению его в
части портфеля, передаваемой перестраховщику.
Список использованных
источников.
1. Мак Томас. Математика
рискового страхования / Пер. с нем. – М.: ЗАО «Олимп – Бизнес», 2005. – 432 с.
2. Хемптон
Д.Д. Финансовое управление в страховых
компаниях – М.: Анкил, 2005. – 263 с.
3. Голубин А. Ю.
Математические модели в теории страхования: построение и оптимизация. – М.:
Анкил, 2003. – 160 с.
4. Бурков В. Н., Заложнев
А. Ю. Механизмы страхования в социально-экономических системах. М.: ИПУ РАН,
2001. – 109 с.