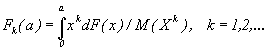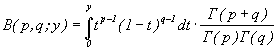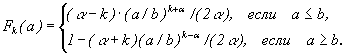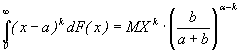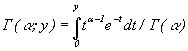Исавнин А.Г.

Камская государственная инженерно-экономическая академия,

Набережные Челны, Россия.

Способы и модели непропорционального перестрахования.

В случае перестрахования при непропорциональном делении риска  размер убытка по первичному риску  составляет

Отсюда сразу следует формула для функции распределения

где F –  функция распределения оригинального размера убытка. Если F(a)<1 (деление риска не фиктивное), то распределение F имеет положительную массу в точке а и поэтому не обладает непрерывной плотностью, даже если таковая существует у исходного распределения F. Для моментов получается выражение

С помощью формулы интегрирования по частям находим

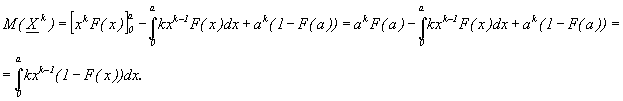
Из определения X непосредственно следуют неравенства  и . Кроме того, посредством дифференцирования по а можно показать, что коэффициент вариации

     и асимметрия     

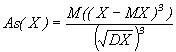
монотонно возрастают по а, и, значит, при F(a) < 1

 .

В этом состоит одно из главных отличий непропорционального деления риска от пропорционального, где коэффициент вариации и асимметрия первичной и вторичной частей убытка совпадают.

При моделировании размера убытка  по вторичному риску, как и при моделировании числа убытков N необходимо учитывать, что убытки размера 0 не причисляются к убыткам. Более точно размер убытка по вторичному риску определяется как

 .

Отсюда следует формула, связывающая функции распределения размеров убытков по первичному и вторичному рискам

 .

При наличии непрерывной плотности f у величины X, также обладает непрерывной плотностью, причем

Согласно этой формуле, при переходе к вторичному риску плотность отсекается слева от точки а, сдвигается влево на а и нормируется таким образом, чтобы площадь под ней снова стала равна 1. Экспоненциальное распределение – единственное непрерывное распределение, инвариантное относительно этих преобразований и удовлетворяющее равенству  для всех  и всех . Если оригинальный размер убытка Х распределен по Парето , то вторичный убыток имеет распределение Парето с нулевой точкой .

Для моментов размера убытка по вторичному риску при условии их существования справедливо выражение

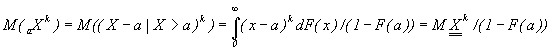
Первый момент  называется средним превышением (границы а). Значение  может быть как больше, так и меньше или равно MХ. Например, в случае экспоненциального распределения  функция  не зависит от а:

а в случае распределения Парето с нулевой точкой  она монотонно возрастает по  а:

 .

Для явного расчета моментов случайных величин X и  или X очень полезна неполная функция моментов

,

обладающая всеми свойствами функции распределения. В таблице 1 приведены неполные функции моментов для некоторых распределений размера убытка.

Таблица 1. Неполные функции моментов.

Логнормальное распределение

Логарифмированное логистическое распределение

где   - неполная бета-функция.

Логарифмированное распределение Лапласа

Распределение Парето с нулевой точкой

 определяется с помощью равенств

   или    .

Распределение Вейбула

 ,  где 

Исследуем влияние непропорционального деления отдельных убытков на совокупный убыток в рамках коллективной модели. Пусть N обозначает число убытков, а  – независимые и одинаково распределенные размеры убытков. Если деление риска осуществляется посредством вычитаемой франшизы а, то на первичный риск по-прежнему приходится N убытков, правда, усеченного размера

.

Под вторичный риск попадает меньшее число убытков

где  – независимые, одинаково распределенные по закону Бернулли случайные величины, . Соответствующие размеры убытков распределены как случайная величина

 ,

где X  распределена как .

Таким образом, совокупный убыток

делится на совокупный первичный риск

и совокупный вторичный риск

    ,

где . Математическое ожидание и дисперсия первичного риска равны:

 .

Для моментов вторичного риска возможны два способа представления (часто бывает удобнее выразить моменты вторичного риска через  и N, чем через и N):

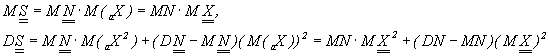
Согласно результатам, приведенным выше:

   ,

где F – функция распределения случайной величины X. Из неравенств X<X и X<X получим:

 

здесь и далее всегда предполагается фактическое деление риска, то есть 0<F(a)<1. Отношение

        

показывает, какая доля ожидаемого убытка и в среднем попадает под франшизу, и называется эффектом освобождения.

Для дисперсий справедливы такие же неравенства, как и для математических ожиданий:

   ,

поскольку    ,

а величины S и S положительно скоррелированы:

   .

Последнее неравенство следует из положительной корреляции величин

   ,

в свою очередь, вытекающей из условий  и

 .

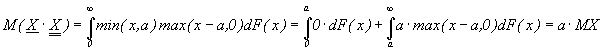В то время как дисперсии величин S, S и S связаны соотношением

   ,

для стандартных отклонений выполняется обратное неравенство

   .

Для доказательства достаточно возвести обе части в квадрат

 и учесть равенство    ,

а также общее свойство коэффициента корреляции случайных величин, не связанных линейной зависимостью .

Свойство особенно интересно в сравнении с соответствующим свойством пропорционального деления риска:

   .

Но более важно следующее свойство непропорционального деления риска.  При непропорциональном делении каждого убытка коэффициенты вариации Vko(S) и Vko(S) первичного и вторичного рисков в рамках коллективной модели являются монотонно невозрастающими функциями от вычитаемой франшизы а, и справедливы неравенства (при условии фактического деления риска)  .

Рассмотрим формы непропорционального перестрахования.

1. Перестрахование эксцедента убытка. По каждому убытку X страховщик выплачивает сумму , ограниченную указанным и договоре максимальным значением , называемым приоритетом, а перестраховщик – сумму , но почти всегда тоже в пределах оговоренного максимума , то есть . Остающаяся после вычета суммы  часть убытка  снова попадает под ответственность страховщика, если не существует другого договора перестрахования эксцедента убытка с приоритетом . Для всех рисков, охваченных одним договором перестрахования, обычно действуют одинаковые значения  и , определяющие правило деления убытков. Размер причитающейся перестраховщику премии зависит от предполагаемого числа и размеров убытков, превышающих , от величины , и, наконец, от договоренности (рисунок 1).

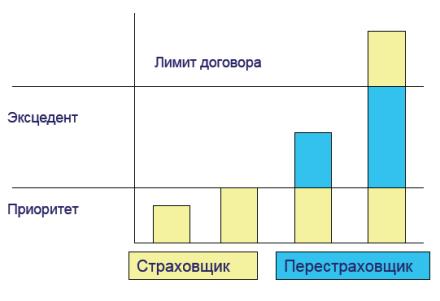
Рисунок 1. Распределение риска при непропорциональном перестраховании.

2. Перестрахование эксцедента кумулятивного убытка отличается от перестрахования эксцедента убытка только тем, что приоритет устанавливается не в отношении отдельного убытка, а в отношении суммы убытков, вызванных одним страховым событием (например, ураганом или землетрясением). Эта форма перестрахования учитывает возможность одновременного наступления (при урагане или землетрясении) большого количества мелких убытков, в совокупности составляющих значительную сумму. Что конкретно следует понимать под отдельным событием, не всегда очевидно, особенно когда несколько событий близки территориально и во времени – соответствующие критерии должны быть четко прописаны в договоре перестрахования.

3. Перестрахование «Stop Loss» представляет собой результат развития принципа перестрахования эксцедента убытка от отдельного убытка через кумулятивный к годовому. Если совокупный годовой убыток S страховщика (по одному виду страхования) превышает установленный приоритет , то перестраховщик принимает часть убытка свыше приоритета, но не более фиксированной величины . Другими словами, страховщик несет убыток  , а перестраховщик – .

При низкой вероятности превышения совокупным убытком границы  (а на практике это чаще всего именно так), «Stop Loss» предоставляет страховщику самую обширную защиту. Ограничивая потенциал убытка страховщика значением , перестраховщик почти полностью принимает на себя технический страховой риск. «Stop Loss» – основная форма перестрахования дочерних компаний материнской.

Таким образом, перестраховываемая часть в большинстве случаев лимитирована. Но лимитированные формы могут быть составлены из нелимитированных основных форм, поэтому в большинстве случаев бывает достаточно исследовать только основные формы.

Перечисленные формы перестрахования часто комбинируются даже в рамках одного вида страхования для одновременной защиты от риска частоты (квотное перестрахование, перестрахование эксцедента кумулятивного убытка, «Stop Loss») и риска большого убытка (перестрахование эксцедента сумм и эксцедента убытка).

Впрочем, стороны могут договариваться о любой форме перестрахования. Встречается, например, перестрахование максимального убытка, когда перестраховщик принимает несколько (допустим, пять) отдельных самых крупных убытков страховщика (возможно, за вычетом франшизы). Правда, подобные формы не приобрели большого практического значения.

 

Список использованных источников.

1.      Мак Томас. Математика рискового страхования / Пер. с нем. – М.: ЗАО «Олимп – Бизнес», 2005. – 432 с.

2.     Хемптон Д.Д.  Финансовое управление в страховых компаниях – М.: Анкил, 2005. – 263 с.

3.     Голубин А. Ю. Математические модели в теории страхования: построение и оптимизация. – М.: Анкил, 2003. – 160 с.

4.     Бурков В. Н., Заложнев А. Ю. Механизмы страхования в социально-экономических системах. М.: ИПУ РАН, 2001. – 109 с.

5.     Гвозденко А. А. Страхование: учеб. – М.: ТК Велби, Изд-во Проспект, 2006. – 464 с.

6.     Конюховский П. В. Математические методы исследования операций в экономике. – СПб.: Питер, 2000. – 208 с.

7.     Кошкин Г. М. Основы актуарной математики: Учебное пособие. – Томск: Томский государственный университет, 2002. – 116 с.

8.     В.В. Шахов. Введение в страхование. 2-е изд. – М., “Финансы и статистика”, 1999.

9.      http://www.infoinsurance.ru

10.  http://www.insur-info.ru