к.т.н. Бельков Д.В.

Донецкий национальный технический университет, Украина

АНАЛИЗ ТРАФИКА КОМПЬЮТЕРНОЙ СЕТИ

При использовании традиционных пуассоновских моделей сетевого трафика наблюдается сглаживание реализации процесса при сжатии временной шкалы, но реальный сетевой трафик проявляет изменчивость на различных шкалах. Он является фрактальным, поскольку обладает свойством самоподобия. Так как инвариантная к масштабу пульсирующая структура трафика оказывает сильное влияние на производительность сети и является характерной особенностью современных телекоммуникационных систем, то учет данного явления при исследовании сетевого трафика является актуальной задачей [1,2].

В данной работе анализ трафика выполнен в среде Excel. Исходные данные представляют собой количество посещений главной страницы yandex.ru (http://stat.yandex.ru/). Полученный временной ряд показан на рисунке 1, он состоит из 30 наблюдений: . Трафик представляет собой ON/OFF процесс переключений между ON состоянием со значительным (свыше ) количеством посещений в будни и OFF состоянием с менее значительным (меньше ) количеством посещений в выходные дни.

На этапе вычислительного эксперимента осуществлен с исходным временным рядом следующий агрегационный процесс. Выполнено уменьшение размера шкалы наблюдений в 2 раза. Для этого сформирован новый ряд, полученный при помощи операции нахождения среднего каждых двух последовательных исходных наблюдений. Полученный ряд состоит из 15 событий. Произошло уменьшение рассматриваемой шкалы в 2 раза: каждое единичное деление новой шкалы содержит 2 единицы исходной. Затем аналогично выполнено уменьшение размера исходной шкалы наблюдений в m раз, для m=3, m=5, m=6 и m=10. Каждое деление новой шкалы содержит m единиц исходной.

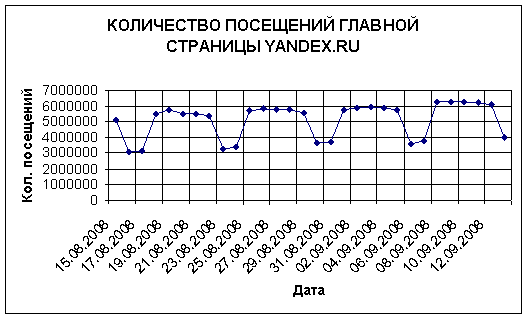
Рисунок 1.- Исходный временной ряд

Согласно определению самоподобного процесса [3], имеет место следующее соотношение дисперсий временных рядов:

(1)

Логарифмируя выражение (1), получим:

(2)

Поскольку является константой, не зависящей от m, то график зависимости от представляет собой прямую с наклоном, равным . Построив график зависимости (2) и линию тренда, как показано на рисунке 2, определим аппроксимированное значение : . Учитывая, что параметр связан с показателем Херста H как [3], получим значение H: H=0,778. Фрактальная размерность D временного ряда в таком случае: .

Параметры самоподобия H и D представляют собой меры устойчивости статистического явления, или меры длительности долгосрочной зависимости стохастического процесса. Значения H=0,5 или D=1,5 указывают на отсутствие долгосрочной зависимости. Чем ближе значение H к 1, тем выше степень устойчивости долгосрочной зависимости.

Рисунок 2.- Линия тренда для определения

В результате исследования трафика посещений главной страницы yandex.ru получено значение показателя Херста H=0,778 и значение фрактальной размерности D=1,222. Поскольку H>0,5, то степень устойчивости долгосрочной зависимости исследуемого временного ряда выше среднего и трафик является самоподобным (фрактальным). Фрактальность трафика вызвана большим количеством конкурирующих соединений и наличием heavy-tailed распределения объемов файлов, передаваемых по сети. Источник пакетов переключается между ON состоянием, в котором происходит передача данных с постоянной интенсивностью, и OFF состоянием молчания.

Необходимо отметить, что анализ трафика можно проводить различными методами. Дальнейшим направлением исследований является корреляционный анализ и R/S-анализ сетевого трафика.

Литература

1. Keshav S. An engineering approach to computer networking. Addison-Wesley,

1997. - 660 p.

2. Кучук Г.А. Учет фрактальных свойств пульсирующего трафика.

//www.nstu/content/_docs/pdf/past/2004/1intel/05/18.pdf.

3. Столлингс В. Современные компьютерные сети.–СПб.:Питер,2003.-328 с.