Шилинец
В.А., Трафимович Ю.В.
Белорусский
государственный педагогический университет
ИССЛЕДОВАНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ТРЕТЬЕГО ПОРЯДКА
В ряде работ ![]() при помощи
гиперкомплексных функций, моногенных в смысле В. С. Фёдорова (
при помощи
гиперкомплексных функций, моногенных в смысле В. С. Фёдорова (![]() -моногенных)
-моногенных) ![]() , исследовались некоторые системы дифференциальных уравнений
в частных производных. В данной работе с помощью
, исследовались некоторые системы дифференциальных уравнений
в частных производных. В данной работе с помощью ![]() -моногенных функций решена краевая задача для одной системы
дифференциальных уравнений в частных производных третьего порядка.
-моногенных функций решена краевая задача для одной системы
дифференциальных уравнений в частных производных третьего порядка.
Пусть ![]() ,
, ![]() – однозначные функции
класса
– однозначные функции
класса ![]() . Считаем эти функции действительными или комплексными, или
гиперкомплексными. В последнем случае предполагаем, что значения этих функций в
области
. Считаем эти функции действительными или комплексными, или
гиперкомплексными. В последнем случае предполагаем, что значения этих функций в
области ![]() являются элементами
какой-нибудь ассоциативной и коммутативной алгебры с единицей над полем
комплексных чисел.
являются элементами
какой-нибудь ассоциативной и коммутативной алгебры с единицей над полем
комплексных чисел.
Предполагаем, что в области ![]() существует
существует ![]() , где
, где ![]() .
.
Как известно ![]() , при этих условиях формальными производными
, при этих условиях формальными производными ![]() ,
, ![]() функции
функции ![]() называются функции от
называются функции от
![]() и
и ![]() , определяемые в области
, определяемые в области ![]() следующим образом:
следующим образом:
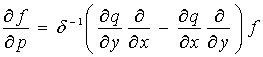 ,
,  .
. ![]()
Пусть ![]() . Тогда определим формальные производные
. Тогда определим формальные производные ![]() ,
, ![]() ,
, 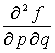 ,
, 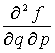 :
:
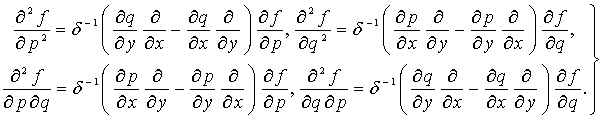
![]()
Аналогично определяются формальные
производные  порядка
порядка ![]() в случае функций
в случае функций ![]() и
и ![]() класса
класса ![]() .
.
Исследуем краевую задачу для следующей
системы дифференциальных уравнений в частных производных третьего порядка:

![]()
где ![]() – искомые комплексные
функции класса
– искомые комплексные
функции класса ![]() .
.
Задача. Найти решение системы ![]() в односвязной области
в односвязной области
![]() , если известны решения этой системы на границе области
, если известны решения этой системы на границе области ![]() – кривой
– кривой ![]() .
.
Решение
краевой задачи. Пусть ![]() ,
, ![]() ,
, ![]()
![]() . Тогда из определений формальных производных получаем
следующую теорему.
. Тогда из определений формальных производных получаем
следующую теорему.
Теорема
1. Система дифференциальных уравнений
в частных производных ![]() эквивалентна
дифференциальному уравнению в формальных производных
эквивалентна
дифференциальному уравнению в формальных производных
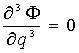 .
.
![]()
Найдём общее решение дифференциального
уравнения ![]() .
.
Теорема
2. Общее решение дифференциального
уравнения в формальных производных ![]() -го порядка
-го порядка
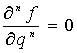 .
. ![]()
имеет вид
![]() ,
, ![]() ,
, ![]()
где ![]() – произвольные
функции, моногенные в области
– произвольные
функции, моногенные в области ![]() относительно функции
относительно функции ![]()
![]() .
.
Доказательство. Как известно ![]() , равенство
, равенство 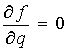 в области
в области ![]() равносильно
моногенности функции
равносильно
моногенности функции ![]() относительно
относительно ![]() в этой области. Таким
образом, теорема для
в этой области. Таким
образом, теорема для ![]() доказана.
доказана.
Допустим сейчас, что теорема справедлива
для ![]() , и докажем её справедливость для
, и докажем её справедливость для ![]() . Действительно, пусть в области
. Действительно, пусть в области ![]() имеем:
имеем:
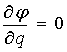
 .
.
Тогда ![]() – моногенная в
области
– моногенная в
области ![]() относительно
относительно ![]() функция и, следовательно,
функция и, следовательно,
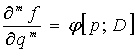 ,
,
откуда получаем
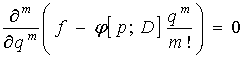 .
.
Но при ![]() мы считаем теорему
справедливой, и потому из последнего равенства следует, что функция
мы считаем теорему
справедливой, и потому из последнего равенства следует, что функция ![]() в области
в области ![]() имеет вид:
имеет вид:
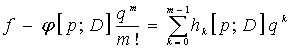 .
.
Тем самым теорема справедлива для ![]() .
.
Таким образом, согласно с теоремой 2 общее
решение дифференциального уравнения ![]() имеет следующий вид:
имеет следующий вид:
![]() ,
,
где ![]() – произвольные
функции, моногенные в области
– произвольные
функции, моногенные в области ![]() относительно функции
относительно функции ![]()
![]() .
.
Легко показать ![]() , что функция
, что функция ![]() , моногенная в смысле В. С. Фёдорова по функции
, моногенная в смысле В. С. Фёдорова по функции ![]() в области
в области ![]() , имеет вид:
, имеет вид:
![]() ,
,
где ![]() – комплексная
функция, аналитическая от
– комплексная
функция, аналитическая от ![]() в области
в области ![]() ;
; ![]() – комплексная
функция, аналитическая от
– комплексная
функция, аналитическая от ![]() в области
в области ![]() .
.
Следовательно, общее решение уравнения ![]() имеет вид:
имеет вид:


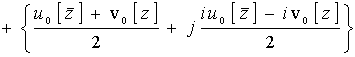 ,
,
где ![]() ,
, ![]() ,
, ![]() – произвольные
комплексные функции, аналитические от
– произвольные
комплексные функции, аналитические от ![]() в области
в области ![]() ;
; ![]() ,
, ![]() ,
, ![]() – произвольные
комплексные функции, аналитические от
– произвольные
комплексные функции, аналитические от ![]() в области
в области ![]() .
.
Отсюда получаем решение системы
дифференциальных уравнений ![]() :
:
![]()
![]() ,
,
![]()
![]() .
.
Так как ![]() ,
, ![]() ,
, ![]()
![]() – произвольные
комплексные функции, аналитические от
– произвольные
комплексные функции, аналитические от ![]()
![]() в области
в области ![]() , то будем считать, что
, то будем считать, что ![]() ,
, ![]() .
.
Тогда решение системы ![]() принимает следующий
вид:
принимает следующий
вид:
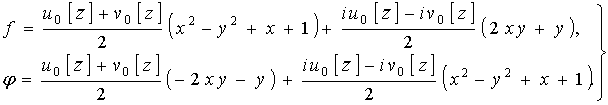
![]()
Отсюда получаем, что
 ,
,
 .
.
Функции ![]() известны на границе
известны на границе ![]() области
области ![]() . Тогда произвольная аналитическая от
. Тогда произвольная аналитическая от ![]()
![]() функция
функция ![]()
![]() будет известна на
кривой
будет известна на
кривой ![]() . Воспользовавшись классической формулой Коши для комплексной
функции
. Воспользовавшись классической формулой Коши для комплексной
функции ![]() по комплексной
переменной
по комплексной
переменной ![]() , а для функции
, а для функции ![]() по переменной
по переменной ![]() , мы найдём значения функций
, мы найдём значения функций ![]() ,
, ![]() внутри области
внутри области ![]() по их значениям на
границе этой области. Тогда из равенств
по их значениям на
границе этой области. Тогда из равенств ![]() определим функции
определим функции ![]() и
и ![]() , удовлетворяющие условиям краевой задачи.
, удовлетворяющие условиям краевой задачи.
Литература
1.
Стельмашук Н.Т., Шилинец
В.А. Метод формальных производных для решения задачи Коши для одной системы
дифференциальных уравнений в частных производных // Дифференциальные уравнения,
1993. – Т.29, № 11. – C. 2019–2020.
2.
Стельмашук Н.Т., Шилинец
В.А. Решение задачи Коши для одной системы дифференциальных уравнений методом ![]() -моногенных функций // Весці НАН Беларусі. Сер. фіз.-мат. навук, 1993. – № 3. –
-моногенных функций // Весці НАН Беларусі. Сер. фіз.-мат. навук, 1993. – № 3. –
С. 108–110.
3.
Стельмашук Н.Т., Шилинец
В.А. Решение краевой задачи для одной системы дифференциальных уравнений в
формальных производных // Весці НАН Беларусі. Сер. фіз.-мат. навук, 1999. – № 3. – С. 127–128.
4. Stelmashuk N.T., Shylinets
V.A. The solution of the boundary value problem for a system of equations in formal
derivatives by means of dual differential operators // Труды института математики НАН Беларуси, 2004. – Т. 12, № 2. – С. 170–171.
5.
Стельмашук Н.Т., Шилинец
В.А. Об интегральном представлении функционально-инвариантных
вектор-аналитических функций // Весці НАН Беларусі. Сер. фіз.-мат. навук, 2006. – № 1. – С. 44–47.
6.
Стельмашук Н.Т., Шилинец
В.А. Об интегральном представлении решений одной системы дифференциальных
уравнений в частных производных // Математическое моделирование и краевые
задачи: Труды пятой Всероссийской научной конференции с международным участием.
Ч. 3. – Самара: СамГТУ, 2008. – С. 162–163.
7.
Стельмашук Н.Т., Шилинец
В.А. О преобразовании к каноническому виду системы линейных уравнений в частных
производных с помощью двойных дифференциальных операторов // Весці НАН Беларусі. Сер.
фіз.-мат. навук, 2008. – № 2. – С. 61–65.
8.
Фёдоров В.С. Основные
свойства обобщенных моногенных функций // Известия вузов. Математика, 1958. – №
6. – С. 257–265.
9.
Гусев В.А. Об одном
обобщении ареолярных производных // Bul. Stiint. si tehnical inst. Pol. Timisoara, 1962. – T. 7, fasc. 2. – P. 223–238.
10. Стельмашук Н.Т. О некоторых дифференциальных
уравнениях в частных производных в дуальной и бикомплексной алгебрах //
Известия вузов. Математика, 1964. – № 3. – С. 136–142.