Математика / 5. Математичне моделювання

Р.О. Жаровський

Тернопільський державний технічний університет імені Івана Пулюя

Ортогональні фільтри Лагера в задачах обробки сигналів.

Вступ.

Відомо, що ортогональні системи функцій відіграють важливу роль в прикладних дослідженнях. Вони служать базисними координатними функціями при передачі сигналів інформації, розкладу сигналів в ортогональні ряди, характеристиками лінійних ланок [1,2].

Основний зміст.

Аналіз відомих ортогональних функцій дискретного аргументу показує, що як імпульсні перехідні характеристики ортогональних фільтрів і ортогональних систем фільтрів можуть бути вибрані ортогональні функції, пов'язані з класичними поліномами. Серед ортогональних лінійних фільтрів широкого використання набули ортогональні фільтри Лагера. Реалізацію фільтрів Лагера будемо розглядати для двох випадків неперервний і дискретний.

В загальному випадку фільтр Лагера складається з каскадного з’єднання лінійних ланок, як показано на рис.1

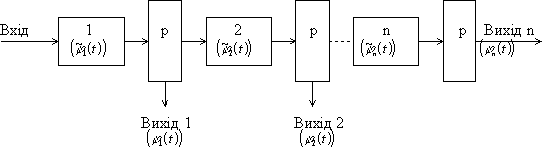
Рис.1. Загальний вигляд фільтра Лагера.

де 1,2,...,n - лінійні ланки з імпульсними реакціями , p - узгоджуюча ланка, необхідна для узгодження підключеного навантаження (зовнішнього кола), а також вхідного і вихідного опорів лінійних ланок фільтра.

При такому каскадному з’єднанні ортогональний фільтр характеризується послідовністю імпульсних перехідних функцій , які формують систему ортогональних функцій. Функція - імпульсна реакція ортогонального фільтра і описується функцією Лагера .

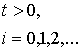
де - ортогональний поліном Лагера.

Поліноми Лагера визначаються наступним чином:

,

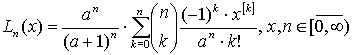Графіки чотирьох поліномів Лагера представлені на рис. 2.

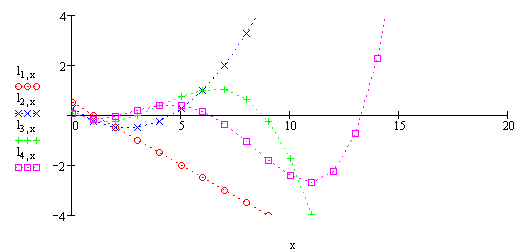
Рис. 2. Поліноми Лагера дискретного аргументу

Завдяки широкому поширенню ЕОМ широке розповсюдження набув аналіз в дискретній формі. Особливо відчутні результати застосування ЕОМ при обробці низькочастотних сигналів, в зв’язку з цим представляє інтерес аналіз з використанням систем ортогональних функцій дискретного аргументу.

Використання корелятора з ортогональними фільтрами Лагера в дискретному варіанті більш повно реалізує всі переваги ортогональної фільтрації, а також забезпечує достатню точність при вимірюванні низькочастотних сигналів.

Основна особливість функцій Лагера дискретного аргументу полягає в тому, що вони забезпечують ортогональність не тільки при нульовому зсуві, але і на всій півосі часових зсувів, що у результаті забезпечує некорельованість на всій півосі зсувів, включаючи початок координат, відгуків ортогональних фільтрів Лагера на дію типу білий шум.

При використанні ортогональних фільтрів і ортогональних систем фільтрів Лагера легко здійснюється компенсація амплітудно-частотної і фазовий-частотної характеристик, викликана їх застосуванням.

Фільтри Лагера — це фільтри низьких частот, і всі їх амплітудно-частотні характеристики не залежать від порядку використовуваного полінома Лагера, що також спрощує компенсацію амплітудно-частотної характеристики.

Висновок.

Дана доповідь присвячена аналізу ортогональних фільтрів, як складних лінійних систем, які в останній час використовуються при статистичній обробці сигналів.

Література

1. Марченко В.Б. Ортогональные функции дискретного аргумента и их приложение в геофизике. – К.: Наукова думка, 1992.- 212с.

2. Марченко Б.Г., Щербак Л.М. Линейные случайные процессы и их приложения. К.: Наукова думка, 1975. - 143 с.